仿射Kähler-Scalar曲率为零的仿射Kähler流形

2015-03-03胡传峰姬秀崔艳丽

商丘师范学院学报 2015年6期

关键词：兰州大学化工学院流形

胡传峰，姬秀,崔艳丽

(1长江大学文理学院基础课部, 湖北荆州 434000;2．防空兵学院训练部，河南郑州450052)

仿射Kähler-Scalar曲率为零的仿射Kähler流形

胡传峰1，姬秀1,崔艳丽2

(1长江大学文理学院基础课部, 湖北荆州 434000;2．防空兵学院训练部，河南郑州450052)

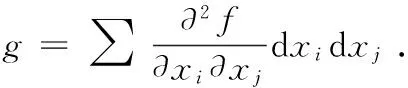
仿射Kähler-Scalar曲率; Hessian流形; 仿射Kähler流形;

0 引言及主要结果

众所周知,J-C-P定理(n=2[1],n≥5[2],[3],)陈述了Monge-Pogorelov方程(1)的任意严格凸光滑解一定是二次多项式.

det(fij)=1.

(1)

设x:M→An+1是由定义在凸域Ω⊂An上的某局部严格凸函数xn+1=f(x1,...,xn)给出的超曲面.李安民和许瑞伟在文献[4]中证明了:若f满足(2),则函数f一定是二次多项式.

(2)

本文我们研究下面的方程

(3)

易知,若f满足(1)或(2),则函数f一定满足(3).方程(2)意味着Kähler-Ricci曲率为零,而(3)意味着Kähler-Scalar曲率为零.

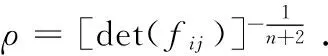
1 基础知识

设f(x1,...,xn)是定义在凸域Ω⊂An上的局部严格凸函数,考虑图超曲面

M={(x,f(x))|xn+1=f(x1,...,xn)}

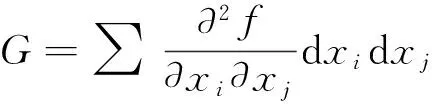
(4)

余法场

U=(-f1,...,-fn,1)

(5)

下面给出一些基本公式[1]相应于度量G的联络有Chistoffel符号

(6)

Fubini-Pick张量Aijk和Weingarten张量满足

(7)

因此有相对Pick不变量

(8)

Gauss积分条件和Codazzi方程是

Rijkl=∑fmh(AmjkAhil-AikmAhjl),

(9)

Aijk,l=Aijl,k,

(10)

由(9)得Ricci张量

Rik=∑fmhflj(AmliAhjk-AikmAhjl),

(11)

定义函数

为了证明主要定理,我们先需证明Φ=0,再利用J-C-P定理.

2 主要定理的证明

由(3)得

(12)

其中

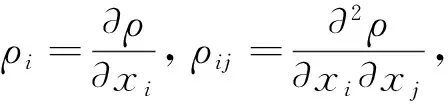
(13)

任取p∈M, 在点p的领域取局部正交标架场, 利用(13)得

设Φ≠0取局部正交标架场使得

ρ1(p)=|gradρ|(p)>0,ρi(p)=0,i>1

则有

(14)

利用(13)及不等式

可得

利用Ricci恒等式得

由上述等式及(14)得

由下述两个方程

可得

进而可得

由

可得

由Δρ≤nρ2及李奇曲率非负可得

两边同时积分得

由M紧致得

Φ=0,利用J-C-P定理得到f一定是二次多项式.

证毕

[1] Jörgens K.Über die Lösungen der Differentialgleichungrt-s2=1[J]. Math. Ann.,1954,127:130-134.

[2] Calabi E.Improper affine hyperspheres of convex type and a generalization of a theorem by K[J]. Jörgens,Michigan Math. J.,1958,5:105-126.

[3] Pogorelov.Av. On the Improper convex affine hyperspheres[J]. Geom. Dedicata, 1972(1):33-46.

[4] Li Anming, Xu Ruiwei. A rigidity theorem for an affine K”{a}hler-Ricci flat graph[J], Result Math.,2009,56:141-164.

[5] Li A M, Jia F. On the Bernstein Property of Affine Maximal Hypersurfaces[J]. Annals of Global Analysis and Geometry, 2003, 23:359-372 .

[6] 秦华军.仿射完备极大曲面的一个结果[J].四川大学学报, 2003(4):637-640.

[7] Li A M, Simon U,Zhao G. Global Affine Differential Geometry of Hypersurfaces, Walter de Grayter [M]. Berlin, New York, 1993.

[责任编辑：王军]

·学术动态·

兰州大学功能有机分子化学国家重点实验室

杨尚东教授莅临我校讲学

2015年4月23日上午，应我校化学工学院邀请，兰州大学功能有机分子化学国家重点实验室学术带头人，有机化学六所所长，博士生导师杨尚东教授在文化路校区化学实验楼三楼学术报告厅作了题为《Phosphine-participated C-H Transformation》学术报告.报告会由应天学者刘澜涛博士主持，化学化工学院部分师生聆听了报告.

杨教授主要从两个方面给大家讲解了他们课题组的研究成果.首先介绍了他们组在过渡金属如铜、银、钯参与下, 通过C—H 键或P—H键活化构建C—P键、C—C键等新型有机合成方法方面的最新研究成果，并简单介绍了他们组如何将成果用于一些药物分子如二期临床抗艾滋病药物IDX899的合成.随后，杨教授又介绍了他的课题组在含磷基团导向的过渡金属催化的交叉偶联方面取得的研究成果.

杨教授语言幽默、逻辑清晰，研究内容新颖前沿.本场精彩的学术报告让大家受益匪浅，博得了全体与会师生的阵阵掌声.报告会上，杨教授与化学化工学院的师生进行了深入的学术交流.

杨尚东，教授、博士生导师，实验室学术带头人，有机化学六所所长.研究兴趣目前主要集中在有机磷化学和不对称C-H键活化方法学研究.1997年本科毕业于兰州大学化学系.1997年至2003年在甘肃省电力科学研究院工作.2006年在兰州大学化学化工学院获得博士学位.2006至2007年在北京大学从事博士后研究并获得中国博士后科学基金一等资助.2007至2009年在美国芝加哥大学从事博士后研究.2009年4月起受聘兰州大学功能有机分子化学国家重点实验室教授，博士生导师.2011年入选教育部 “新世纪优秀人才支持计划”.2013年获得国家自然科学二等奖(排名第四)和中国百篇最具影响国际学术论文奖.2015年获得Thieme Chemistry Journal Award奖.2014年开始担任《中国化学快报》青年编委.已在J. Am. Chem. Soc., Angew. Chem. Int. Ed., Org. Lett., Chem. Commun., Chem. Eur. J.等刊物上发表SCI论文40余篇.

On affine Kähler manifolds with zero affine Kähler-Scalar curvature

HU Chuanfeng1, JI xiu1, CUI Yanli2

(1.Yangtze University College of Arts and Science,Jingzhou 434000, China;2.Department Training of the Air Defense College, Zhengzhou 450052, China)