一种基于改进BTS的多类非平衡分类的集成学习方法

汤志亚，赵亮，杨玲，甄小琼，杨志鹏

(1. 成都信息工程学院，四川 成都 610225；2. 中国气象局大气探测重点开放实验室，四川 成都 610225)

一种基于改进BTS的多类非平衡分类的集成学习方法

汤志亚1,2，赵亮1,2，杨玲1,2，甄小琼1,2，杨志鹏1,2

(1. 成都信息工程学院，四川 成都 610225；2. 中国气象局大气探测重点开放实验室，四川 成都 610225)

提出一种适用于多类不平衡数据的集成学习方法，以解决多类样本分布不均衡问题.首先，利用合成少类样本的过采样技术(Synthetic Minority Over-sampling Technique, SMOTE)得到一组类别平衡的训练集.然后，对每个训练集采用二叉树支持向量机(SVM of Binary Tree，BTS)进行训练，最后，采用Bagging进行集成.通过5组UCI测试数据表明该算法在Gmean参数上比SMOTEBagging算法提高2.55%.

多类不平衡分类；集成方法；二叉树支持向量机；SMOTE算法

0 引 言

类别非平衡学习问题是数据挖掘领域研究的重要课题之一.所谓类别非平衡学习问题是指在分类过程中，少数类样本的误判率通常比多数类样本的误判率高很多[1].近年来，在类别非平衡学习问题中，集成方法以其高效的性能，被广泛用于提高现有方法或者帮助形成新的方法[2]，由此也越来越受到研究人员的青睐.

目前，集成方法大致分为三类：Bagging、Boosting和不同组合策略相结合的组合方法[3].集成方法主要是通过重采样方法与集成方法相结合的方法来处理非平衡数据.例如文献[4]提出的SMOTEBagging.文献[5]提出的SMOTEBoost和文献[6]提出的RUSBoost，以及文献[7]提出的EasyEnsemble和BalanceCascade.

但是，上述方法中，只有SMOTEBagging方法可直接用于多分类，其余方法只适用于二分类.并且在SMOTEBagging算法中以决策树作为基分类器，稳定性欠佳.BTS是由文献[8]于2004年提出的一种新的用于多分类的分类器，以其稳定性和高效性而得到广泛的应用.但是其对非平衡数据集的分类不理想.因此，本文结合SMOTE算法和BTS算法，形成一种新的适用于多类非平衡数据集的分类器，称为SMOTE-BTS.并且在此基础上将该分类器进一步采用Bagging算法进行集成，提出一种新的适用于多类别非平衡数据分类的集成算法，称为SMOTE-BTS-Bagging.

1 二叉树支持向量机

1.1 支持向量机

SVM通常用于二分类问题.以二分类情况为例，假设两类训练样本集为{(x1,y1),(x2,y2),…,(xn,yn)},yi∈{+1,-1},i=1,2,…,n为样本标签.

构造代价函数为：

(1)

约束条件为：

yi(wTxi+b)≥1-ξi,ξi≥0,i=1,2,…,n

(2)

其中：ξi称为松弛变量；C称为惩罚因子，用来控制关联项的相对影响；w和b分别表示分类函数f(x)=wTx+b的权向量和阈值.则相应的拉格朗日函数为：

(3)

其中λi和μi是拉格朗日算子.对应的最优化条件为：

λi[yi(wTxi+b)-1+ξi]=0,i=1,2,…,n;

(4)

C-μi-λi=0,i=1,2,…,n.

(5)

μiξi=0,i=1,2,…,n

(6)

最终求解分类函数为：

1.2 二叉树支持向量机

传统SVM进行多分类的方法大致分为3种：One-against-all、One-against-one和无向环图法[9].针对SVM进行多分类的问题，近年来，一些学者提出一种基于二叉树的支持向量机(Binary Tree of SVM，简称BTS)越来越受到人们的关注[8～10].同传统的二分类转多分类的方法相比，BTS结构具有高准确率，快速，并且能够避免类别不可分和分类重叠等优点[10].

其主要思想是：将所有类别分成两个子类，再将两个子类分别划分成两个次级子类，依次类推，直到所有的节点只含有一个类别为止.这样，多分类问题就转化为二分类问题，每个节点处采用SVM二值分类器作为分类函数.

2 SMOTE-BTS-Bagging算法

本文采用Bagging集成学习方法，以SMOTE-BTS作为基分类器，形成一种新的适用于多分类非平衡数据的集成分类算法，称为SMOTE-BTS-Bagging算法.

2.1 SMOTE-BTS分类器

本文结合SMOTE算法[11]和BTS算法，形成一种新的解决多类非平衡数据集的分类算法，称为SMOTE-BTS算法.该分类算法中除了采用SMOTE算法增加样本的平衡性，还采用随机过采样技术使得BTS算法中每个非叶子节点左右两个训练集达到平衡.

算法主要思想：首先，采用SMOTE算法使得原始训练集S中每一类的样本数目相等，此时得到平衡训练集Sk；然后，采用BTS算法进行训练，得到一个分类器；最后，采用该分类器进行分类预测.

2.2 SMOTE-BTS-Bagging算法

Bagging作为一种新的高效集成算法，应用范围变得越来越广泛[12].作为集成分类方法中的基分类器，要求识别率高和多样性[13].这样才能使得集成之后的分类器成为一个强分类器.而SMOTE-BTS正是这样一种分类器，基于上述原则，兼顾对不平衡数据集的适应性.本文以SMOTE-BTS为基分类器，采用Bagging进行集成，形成一种新的适应于多类非平衡数据分类的集成算法，简称为SMOTE-BTS-Bagging算法.

SMOTE-BTS-Bagging算法流程：

(1)训练：

1.设原始训练集为S；

2.按照每一类的样本数目，由小到大排列重新组成训练集Snew；

3.按照下面的规则构建一个训练集Sk，此训练集中所有类别的样本数目相等：

3a 设样本最多的一类为M；

3b 对于每一类i(i=1,…,M-1)，

以(Nm/Ni)*b%的比例采用可重复采样技术，对第i类进行采样；

设置N=(Nm/Ni)*(1-b%)*100，

采用SMOTE(K,N)生成新的样本；

4.采用Sk训练一个SMOTE-BTS模型；

5.改变b的值；

6.重复步骤3到5，直到运行次数等于NumTree.

(2)测试新样本：

1 .生成每一个SMOTE-BTS分类器的输出；

2.返回得到最多投票的类别.

其中NumTree表示基分类器的个数.参数b是为了增加训练集的多样性，同时也会使得SMOTE-BTS的分类器变得多样性.一般如果NumTree=10，则b的变化范围以10为间隔由10变到100.

3 类别非平衡分类的评价方法

传统的分类器一般会以整体的准确率作为评价标准，由于非平衡数据中少数类的准确率通常占据更重要的地位，因此它不再适用于不平衡数据分类问题.文献[14]中提出的平衡查准率(balanced accuracy rate，简称BArate)和文献[15]提出的F-measure两个参数能够有效地衡量二分类非平衡数据的分类性能.文献[16]提出的Gmean可以有效测试多类别非平衡数据的分类性能.

如果用TP表示实际为正类被预测为正类的样本个数，TN表示实际为负类被预测为负类的样本个数，FP表示实际为负类被预测为正类的样本个数，FN表示实际为正类被预测为负类的样本个数.其中正类表示少数类，负类表示多数类.那么：

BArate=TP/(2(TP+FN))+TN/(2(TN+FP))

(7)

(8)

(9)

(10)

Gmean具体定义如下：设样本集类别的总数目为N，分类器将i类样本错分为j类的样本数目为Kij，则类别i的查全率的表达式为：

(11)

查全率的几何平均值表达式为：

(12)

4 实验结果与分析

为了验证本文所提出算法的有效性，本节分别采用3组UCI两类不平衡数据集和4组UCI多类不平衡数据集进行验证，全部数据均在UCI上下载，下载网址是http://archive.ics.uci.edu/ml/.实验设计思路如下：首先，选择3组UCI中的两类非平衡数据，同目前处理不平衡数据的主要集成方法进行对比，来验证本算法的有效性和优越性.然后，使用4组UCI多类非平衡数据测试本算法，同可用于多类非平衡数据的SMOTEBagging算法作对比，来进一步验证本文提出算法在多类非平衡数据集分类上的优越性.

4.1 两类非平衡数据分类

表1 两类UCI数据使用说明

本文选取pima，solarflare和balance 3组UCI测试数据进行试验.与本文提出的SMOTE-BTS-Bagging算法作对比的集成分类方法有SMOTEBagging、SMOTEBoost、RUSBoost、EasyEnsemble和BalanceCascade.采用5折交叉验证得到BArate、Gmean和F-measure 3个参数的测试值.3组数据的测试结果分别如图1、图2、图3所示：

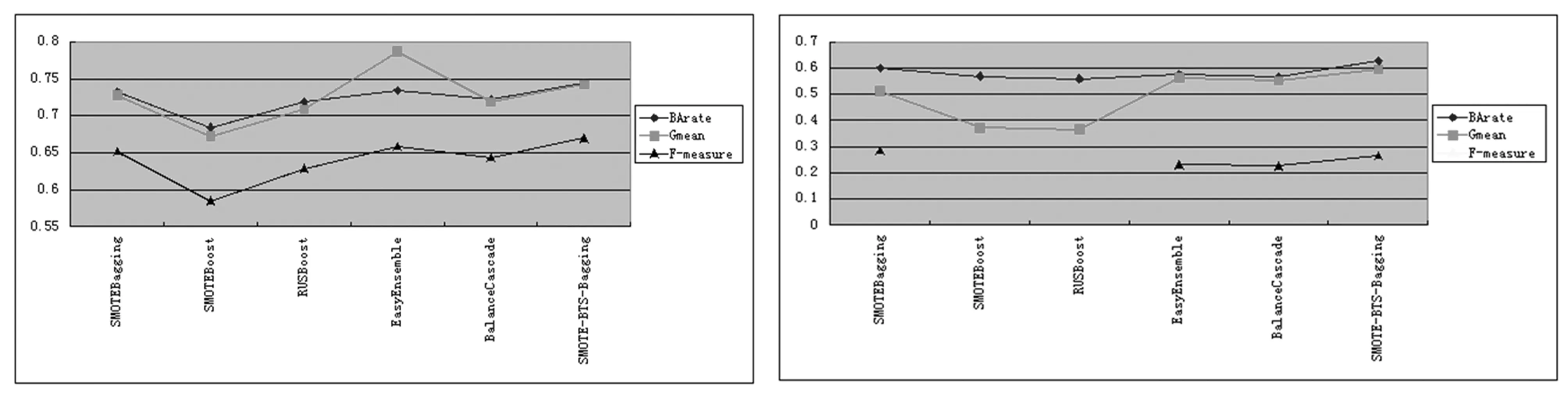
图1 Pima数据测试结果 图2 Solarflare数据测试结果

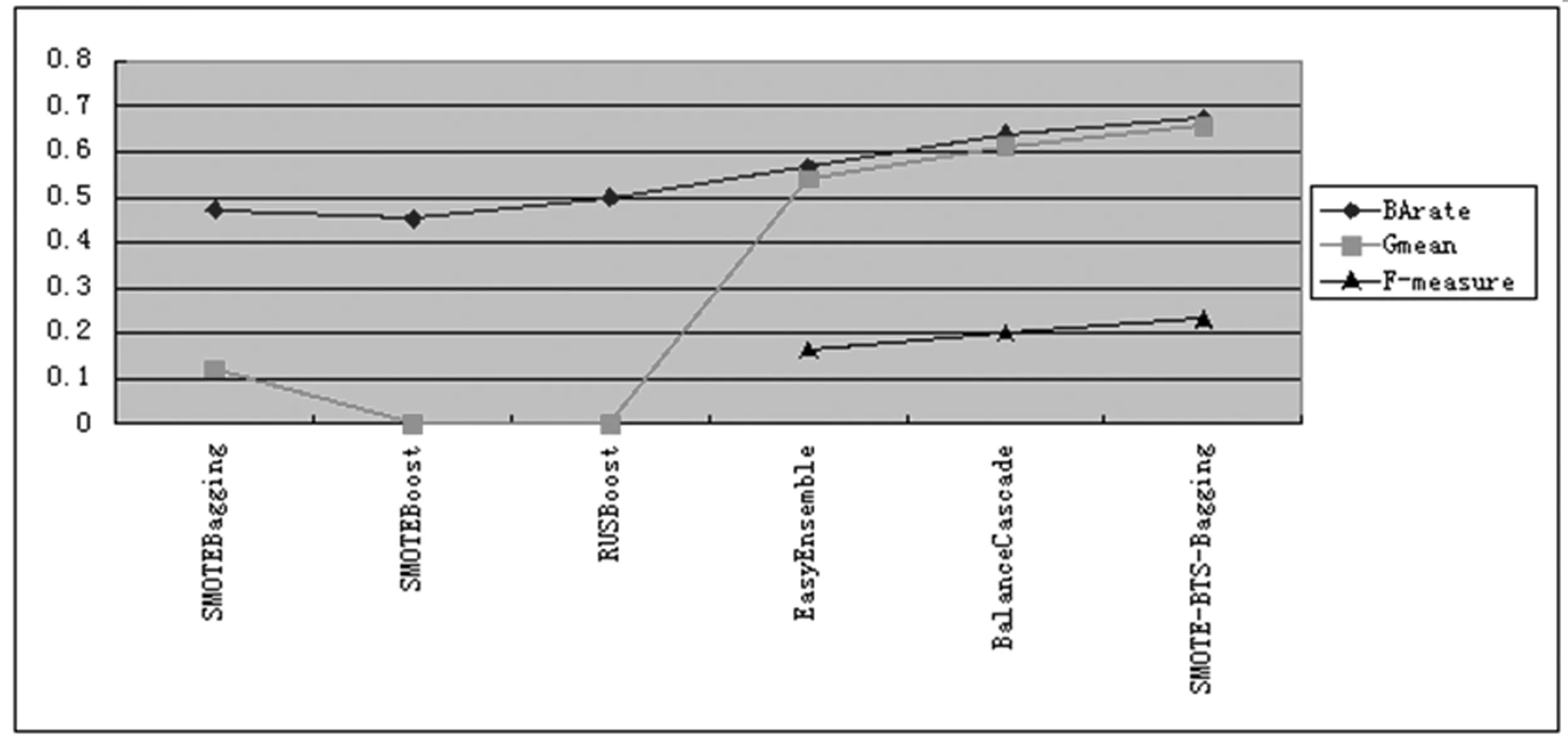
图3 Balance数据测试结果

如图1、图2、图3所示，3组UCI测试集中，本文提出的算法只有在F-measure参数上的性能略差，3组数据中，有2组数据该参数取得最高值.在BArate和Gmean两个参数中，本文提出的算法在3组数据上均取得最高值.从而证明了本文所提出算法针对两类非平衡问题，同其他几种集成算法相比，具有更好的分类性能.

4.2 多类别非平衡数据分类

采用UCI中的glass、new_thyroid、ecoli和yeast 4组多类非平衡数据集进行测试.上述对比的几种集成算法中只有SMOTEBagging算法可直接应用与多类别分类.因此本节中将本文提出的算法与SMOTEBagging、BTS和SMOTE-BTS对比，并采用5折交叉验证得出Gmean参数值.

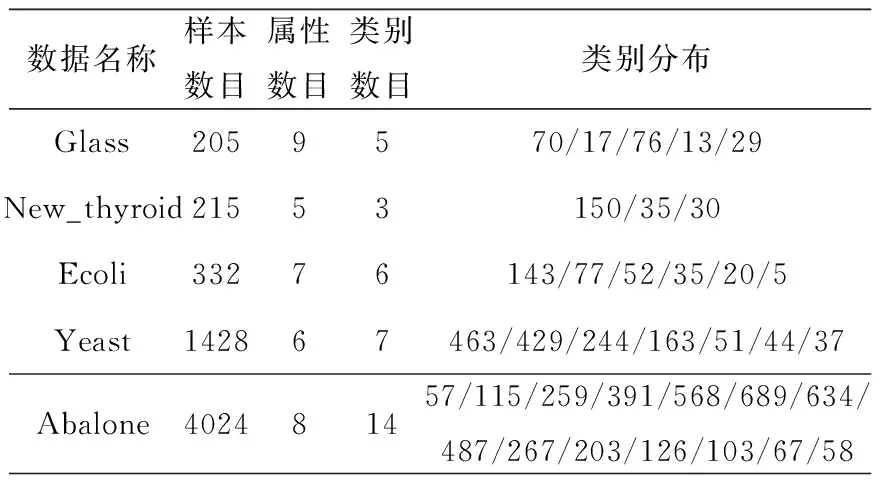
表2 多类UCI数据使用说明

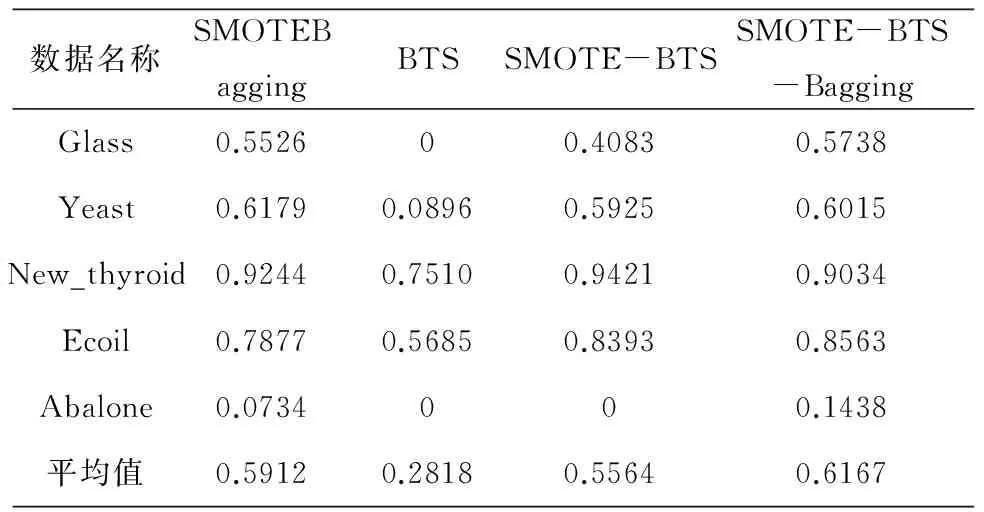
表3 Gmean参数测试结果

由表3可以看出，在多类非平衡数据分类中，本文中的SMOTE-BTS算法在5组数据上，Gmean值均高于BTS算法，从而证明SMOTE-BTS算法更适用于多类非平衡数据.采用Bagging集成方法进一步提出的SMOTE-BTS-Bagging算法在5组测试数据中，有3组数据取得最优，而SMOTEBagging和SMOTE-BTS各在一个数据中取得最优.进一步对比所有数据的平均Gmean值，发现SMOTE-BTS-Bagging算法比其它算法更具有优势，其平均Gmean值为61.67%，而SMOTE-BTS与SMOTEBagging算法的Gmean值分别为55.64%和59.12%，分别提高了6.03%和2.55%.

5 结束语

为了解决多类样本非平衡问题，本文提出一种基于改进BTS的多类非平衡分类集成算法，即SMOTE-BTS-Bagging方法，该方法结合SMOTE和BTS算法，并采用Bagging算法进行集成.在处理多类别非平衡数据集时，比其它算法在性能参数上有一定的提高.但是，BTS算法中参数的优化以及与其它重采样技术的结合仍需要进一步的研究.

[1] Liu X Y, Wu J, Zhou Z H. Exploratory undersampling for class-im- balance learning[J]. Systems, Man, and Cybernetics, Part B: Cyber- netics, IEEE Transactions on, 2009, 39(2): 539-550.

[2] HE H, MA Y. Imbalanced learning: foundations, algorithms, and a- pplications[M]. Wiley. com, 2013.

[3] Zhou Z H. Ensemble methods: foundations and algorithms [M]. C- RC Press, 2012.

[4] Wang S, Yao X. Diversity analysis on imbalanced data sets by usin- g ensemble models[C].Computational Intelligence and Data Mining, 2009. CIDM′09. IEEE Symposium on. IEEE, 2009.324-331.

[5] CHAWLA N V, LAZAREVIC A, HALL L O, et al. SMOTEBoost: Improving prediction of the minority class in boosting[M].Knowle- dge Discovery in Databases: PKDD 2003. Springer Berlin Heidelb- erg, 2003.107-119.

[6] SEIFFERT C, KHOSHGOFTAAR T M, VAN HULSE J, et al. RU- SBoost: A hybrid approach to alleviating class imbalance[J]. Syste- ms, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 2010, 40(1): 185-197.

[7] LIU X Y, WU J, ZHOU Z H. Exploratory undersampling for class- imbalance learning [J]. Systems, Man, and Cybernetics, Part B: Cy- bernetics, IEEE Transactions on, 2009, 39(2): 539-550.

[8] CHEONG S, OH S H, LEE S Y. Support vector machines with bin- ary tree architecture for multi-class classification[J]. Neural Inform- ation Processing-Letters and Reviews, 2004, 2(3): 47-51.

[9] MADZAROV G, GJORGJEVIKJ D, CHORBEV I. A multi-class S- VM classifier utilizing binary decision tree[J]. Informatica(Sloveni- a), 2009, 33(2): 225-233.

[10] FEI B, LIU J. Binary tree of SVM: a new fast multiclass training and classification algorithm[J]. Neural Networks, IEEE Transactions on, 2006, 17(3): 696-704.

[11] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthe- tic minority over-sampling technique[J]. Journal of Artificial Intelli- gence Research,2002,16(1):321-357.

[12] YAO D, YANG J, ZHAN X. An improved random forest algorithm for class-imbalanced data classification and its application in PAD risk factors analysis[J]. Open Electrical & Electronic Engineering Journal, 2013, 7(1): 62-70.

[13] HANSEN L K, SALAMON P. Neural network ensembles[J]. Patte- rn Analysis and Machine Intelligence, IEEE Transactions on, 1990, 12(10): 993-1001.

[14] HONES T R. Living in an imbalanced world[D]. University of Notre Dame, 2012.

[15] HE H, GARCIA E A. Learning from imbalanced data [J]. Knowled- ge and Data Engineering, IEEE Transactions on, 2009, 21(9): 1263-1284.

[16] 霍纬纲,高小霞. 一种适用于多类不平衡数据集的模糊关联分类方法[J].控制与决策,2012,27(12):1833-1838.

[责任编辑：王军]

An ensemble classification method for multi-class imbalanced datasets

TANG Zhiya1,2, ZHAO Liang1,2,YANG Ling1,2,ZHEN Xiaoqiong1,2,YANG Zhipeng1,2

(1. Chengdu University of Information Technology, Chengdu 610225,China;2. CMA.Key Laboratory of Atmospheric Sounding，Chengdu 610225,China)

To solve the problem of multi-class imbalanced datasets classification, an ensemble classification method for multi-class imbalanced datasets is presented. Firstly, we get balanced datasets by using the SMOTE algorithm. Then, we utilize the binary tree of SVMs to get the models for every training dataset. Finally, we make an ensemble with bagging method for the models. The result showed that compared with SMOTEBagging, our method improved 2.55% on the Gmean value to five UCI multi-class imbalanced benchmark datasets.

multi-class imbalanced dataset; ensemble method; Binary tree of SVM; SMOTE algorithm

2015-03-19

科技部公益性行业(气象)科研专项课题(GYHY201106047)支持

汤志亚(1977-)，男，河南商丘人，成都信息工程学院讲师，硕士，主要从事气象探测技术的研究.

TP391

A

1672-3600(2015)06-0030-05