应力比对K55套管钻井钢疲劳裂纹扩展性能的影响
2015-03-03许天旱冯耀荣雒设计王党会
许天旱,王 荣,冯耀荣,雒设计,王党会,杨 宝
(1 西安石油大学 材料科学与工程学院,西安 710065;2 中国石油集团 石油管工程技术研究院,西安 710065)
应力比对K55套管钻井钢疲劳裂纹扩展性能的影响
许天旱1,王 荣1,冯耀荣2,雒设计1,王党会1,杨 宝1
(1 西安石油大学 材料科学与工程学院,西安 710065;2 中国石油集团 石油管工程技术研究院,西安 710065)
利用电液伺服疲劳实验机及 SEM 研究了应力比对 K55 套管钻井钢疲劳裂纹扩展行为的影响。结果表明:应力比对裂纹失稳区起始点对应的应力强度因子范围ΔK值具有显著的影响。随着应力比的增加,裂纹扩展失稳区起始点对应的裂纹扩展速率具有显著的降低,疲劳裂纹扩展门槛值也呈现显著的降低趋势。当疲劳裂纹逐渐由Paris区过渡到失稳扩展区,平均载荷逐渐取代应力强度因子幅度ΔK作为裂纹扩展的主导驱动力。当裂纹扩展至拉伸过载区,断口表面则呈现明显的冲击断裂特征。
K55套管钻井钢;应力比R;疲劳裂纹扩展性能;应力强度因子范围ΔK;断口形貌
套管钻井作为一种新技术,主要用于解决钻井过程的稳定性及降低钻井成本问题[1-4]。随着套管钻井技术的发展,套管所面临的环境越来越苛刻[5]。由于套管除了固井同时兼有钻井的作用,导致套管及其接箍被置于一种复杂的动载工况下,套管疲劳失效等问题变得日益突出。目前,套管钻井技术方面的研究主要集中于钻井技术和相关的装备方面,如解决套管的丝扣、密封等方面问题。保证钻井安全采取的措施主要是选用高强度大壁厚套管,这无疑浪费了材料,提高了成本。因为在API Spec 5CT 套管和油管规范中,虽然对于套管材料的屈服强度、抗拉强度及伸长率给予了明确规定,但对套管材料的疲劳裂纹扩展性能并没有给出强制性规定,这主要是因为套管过去仅仅用于固井,一般不考虑动态载荷和疲劳裂纹扩展。而现在,随着套管钻井技术的出现,套管由(准)静态载荷转变为包括冲击、振动和疲劳载荷等的动态载荷。例如:在钻进过程中,由于地貌复杂,尤其是地质结构为黏性构成的作用下,钻具不能连续稳速的钻进,而发生振动,速度快慢相间,极易产生疲劳。同时,在套管钻井过程中,管柱把扭矩和动力传递给钻具[6]。或者因为扭矩不合适,或者因为套管性能的降低,套管经常损伤、断裂[7],这使得套管疲劳失效等问题变得更加突出。K55套管钻井钢因其较低的成本和简单的生产工艺,同时具有较高的硬化指数[8],在套管钻井技术研究中得到广泛的应用。尽管目前国内外对于各种材料的疲劳性能研究较多[9-12],但因套管钻井技术尚处于探索阶段,对于套管钻井钢疲劳性能的研究报道较少。本工作系统研究了应力比对K55套管钻井钢疲劳裂纹扩展性能的影响,对不同裂纹扩展阶段断口形貌进行了观察,并分析了不同应力比对不同裂纹扩展阶段裂纹扩展速率影响的机理,同时解释了不同特征断裂表面形成的机理,为套管钻井技术的发展和改善提供依据。
1 实验材料及方法
1.1 实验材料
本实验所用材料均以接箍形式由中国石油集团石油管工程技术研究院提供,直径为244.48mm,厚度为11.43mm。材料的化学成分和力学性能如表1和表2所示,满足API Specification 5CT 要求。试样从接箍上截取,截取和加工保证不影响材料性能。

表1 K55钢的化学成分(质量分数/%)

表2 K55钢的力学性能
1.2 实验方法
疲劳实验采用CT试样,试样厚度为4.8mm,宽度W=30mm,满足ASTM E647标准,取样位置及示意图如图1所示。实验进行之前,首先对CT试样进行预裂,预裂长度为2mm。疲劳裂纹扩展实验是在PDL-100型液压伺服疲劳实验机上进行的,实验温度为室温,频率为10Hz,加载波形为正弦波型,最大载荷为1.4kN,实验应力比R=Pmin/Pmax,分别为:0.1,0.3,0.5,0.7。裂纹长度由微机辅助电位法监测,电位函数由边界元法计算给出[13]。
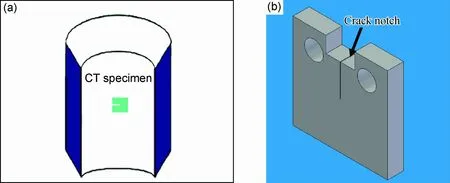
图1 CT试样取样位置及示意图 (a)取样位置示意图;(b)试样示意图Fig.1 Fatigue CT test sample scheme (a)specimen sectioned from the coupling of casing-drilling steel;(b)the line drawing of the specimen
疲劳裂纹门槛值的确定采用降载法,分级降载百分比保持在5%,同时保证每级载荷下裂纹扩展量是上一级载荷下塑性区尺寸的4~6倍,直到疲劳循环1×106次裂纹不发生0.1mm扩展为止,对应的ΔK即为对应的裂纹扩展门槛值。为了研究和确定不同裂纹扩展区的断裂机制,试样从疲劳断口中心平行于裂纹扩展方向且垂直于断口切开,利用SEM研究裂纹扩展路径和微观断裂机制。
2 实验结果及分析
在(da/dN)-ΔK关系曲线中,不同应力比R下的裂纹扩展性能具有显著的区别如图2所示。当ΔK为23MPa·m1/2时,对于R=0.1和R=0.3,(da/dN) 处于低Paris区,对于应力比为R=0.5来说,(da/dN) 正好处于Paris区中部。而对于R=0.7来说,(da/dN) 已经到了快速扩展区。同时类似的现象也出现在其他类型合金的(da/dN)-ΔK关系曲线中。这种趋势和其他相似合金研究的结果基本是一致的[14]。从图2中也可以看出应力比对试样进入裂纹快速扩展区的临界ΔK影响是十分显著的,对于试样最终撕裂点ΔK的影响也十分显著。

图2 不同R下的da/dN与ΔK之间的关系曲线Fig.2 Relationship between da/dN and ΔK at different R
同时从图2中也可以看出,随着应力比的增大,进入裂纹快速扩展区的起始ΔK值越来越小,相同ΔK处对应的裂纹扩展速率越来越大。而且当应力比从0.1增加到0.3,进入裂纹快速扩展区和进入撕裂区的ΔK相差不大,当应力比从0.3增加到0.5,进入裂纹快速扩展区和进入撕裂区的ΔK都急剧降低。这主要是因为,随着应力比的增加,裂纹扩展的机制发生了变化。当应力比较低时,在加载时裂纹完全张开,在卸载时裂纹闭合的程度与大应力比相比更明显,闭合效应起到重要的作用。因此当应力比由0.1增加到0.3,各参数变化幅度较小;当应力比超过0.5,闭合效应减弱,不再起主导作用,因此,随着应力比继续升高,各参数发生急剧变化。
从图2中也可看出,不同应力比下裂纹扩展曲线的线性区平行,裂纹扩展曲线线性区的斜率仅仅与材料本身有关,与实验参数无关,通过分析,da/dN和ΔK之间关系满足Paris关系式:
da/dN=CΔKm
(1)
式中:da/dN为疲劳裂纹扩展速率,m/cycle;m和C为材料常数;ΔK为应力强度因子幅度,MPa·m1/2。裂纹扩展曲线线性区的斜率对应于Paris常数的m,m和另外一个材料常数C如表3所示。
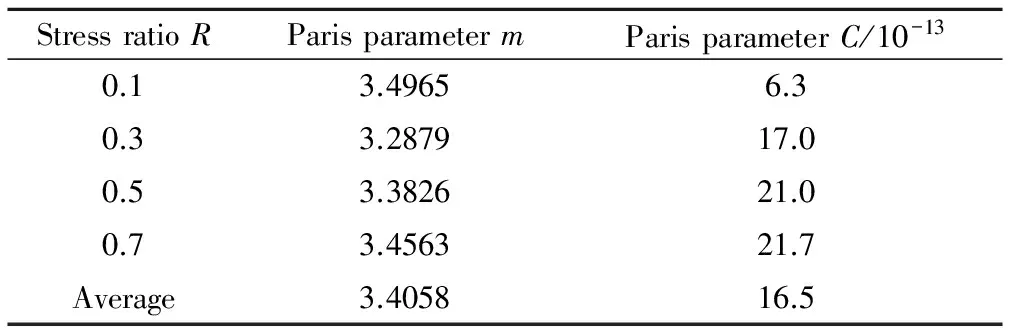
表3 K55套管钻井钢的材料参数
从实验结果的拟合值看出,m的平均值为3.4058,这与相关文献的报道是一致的,典型金属的Paris指数m在2~4之间[15]。从图中的曲线也能看出,随着应力比R的增大,(da/dN)-ΔK曲线向上移动。这是因为计算ΔK和绘制曲线时,没有考虑到裂尖闭合效应的影响,K55套管钻井钢伸长率达到18.49%,因此在每一次载荷循环过程中,裂尖都会发生塑性变形,引起闭合效应,因此实际有效应力强度因子幅值更小,因此随着R的增加,(da/dN)-ΔK曲线发生上移。
从图2中也可看出,应力比对裂纹扩展失稳区起始点对应的ΔK值具有显著的影响。应力比和裂纹失稳区起始点对应的ΔK值之间的关系如图3所示,发现他们之间呈显著的线性关系,用最小二乘法拟合可获得如下公式:
ΔKus=88.431(1-1.043R)
(2)
式中:ΔKus为疲劳裂纹扩展失稳区起始点对应的ΔK值,MPa·m1/2
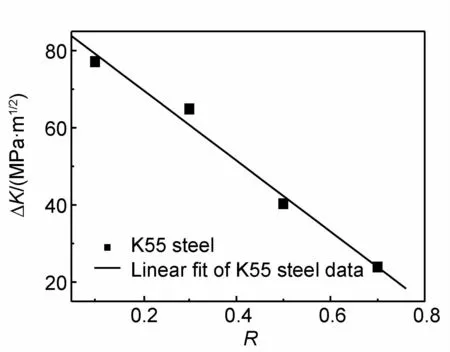
图3 应力比R和裂纹失稳区起始点对应的ΔK值之间的关系Fig.3 Relationship between stress ratio R and ΔK corresponding starting point of crack unstable zone
从拟合效果来看,疲劳裂纹失稳区起始点对应的ΔK值和应力比之间线性相关性很高,相关系数为0.9927。式(2)中88.431MPa·m1/2对应于应力比为0时的疲劳裂纹失稳区起始点对应的ΔK值。式(2)中应力比R前的系数1.043则取决于材料本身性质。材料不同,对应的ΔK值对R的敏感程度不同。随着应力比的增加,材料疲劳裂纹失稳区起始点对应的ΔK值降低。这归因于在裂纹扩展中平均载荷逐渐取代应力强度因子幅度起主导作用,这个主导因素的转换从疲劳断口由疲劳条带断裂机制逐渐转换为类似拉伸断口,再转换为类似解理断口得到证明,如图4所示。图4显示出了K55钢不同裂纹扩展阶段的疲劳断口形貌,从图4(a)中可看出,在门槛区,疲劳断口表面相对比较平整,由图4(b)和图4(c)可见,Paris区疲劳断口具有明显的疲劳条带,与门槛区断口有着显著区别,且随着疲劳裂纹扩展条带宽度逐渐增加,这些条带相比铝合金、钛合金,条带显著更粗糙,这是由钢铁材料较差的延性所决定的。由图4(c)可见,疲劳条带宽度约为1.1μm,可估算出对应的疲劳裂纹扩展速率约为1.1×10-6m/cycle,这与实验结果也是一致的,位于K55钢(da/dN)-ΔK曲线的上Paris区,为中Paris区裂纹扩展速率的两倍多。当裂纹扩展进失稳区,断口表面的上疲劳条带特征消失,呈现出显著的韧窝特征,类似于拉伸断口的特征,区别在于疲劳断口上的韧窝具有显著的方向性,如图4(d)所示,这说明疲劳裂纹扩展机制发生转变,由应力强度因子幅度主导的双滑移机制转变为平均载荷主导的拉伸断裂机制,在疲劳裂纹扩展过程中,试样上所施加的平均载荷可按如下公式计算:
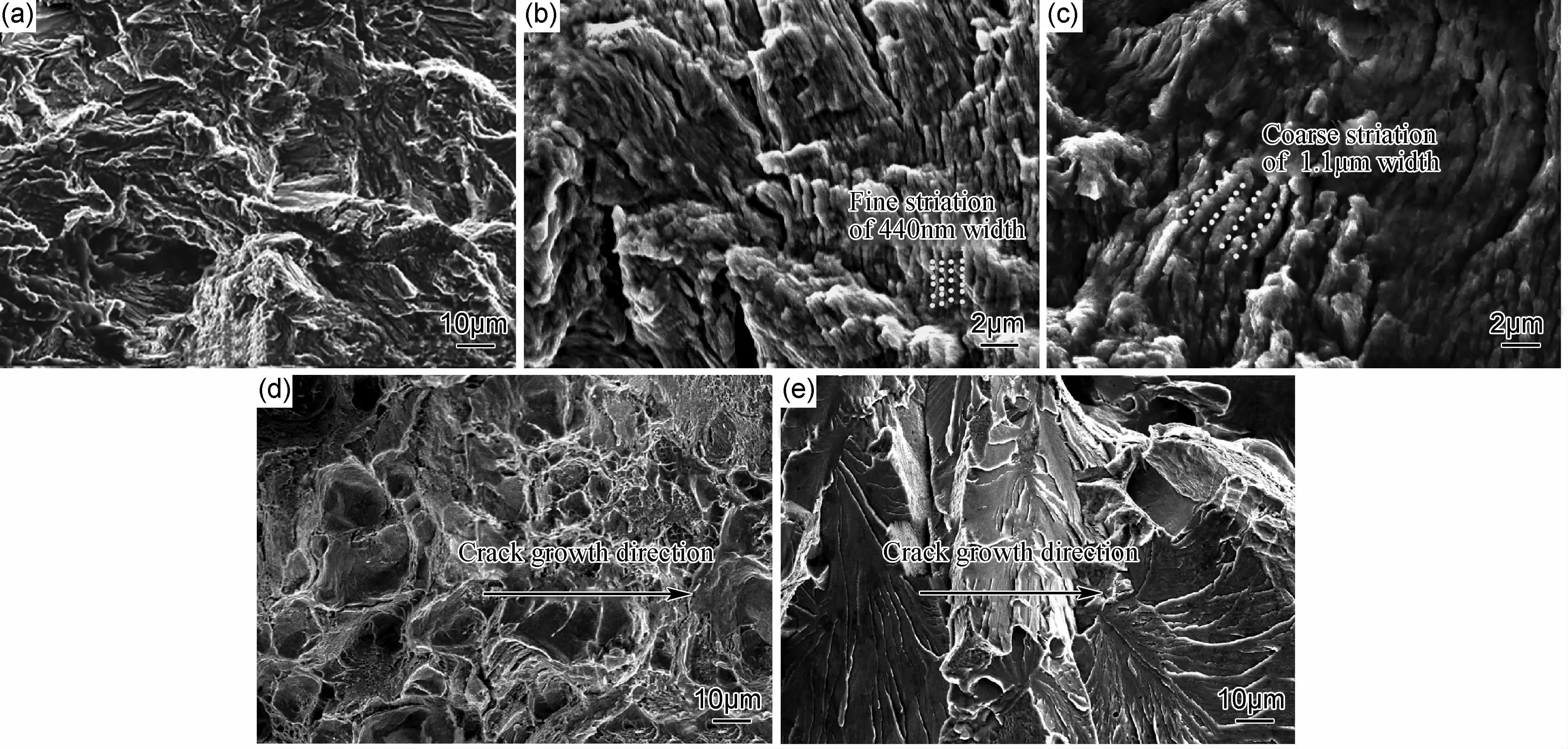
图4 K55钢疲劳断口 (a)门槛区;(b)Paris区;(c)上Paris区;(d)失稳区;(e)拉伸过载区Fig.4 Fatigue fracture surface of K55 steel (a)threshold region;(b)Paris region;(c)upper Paris region; (d)unstable zone;(e)overload tensile zone
(3)
式中:Pmean为平均载荷,kN;Pmax为最大载荷,kN;Pmin为最小载荷,kN。
由公式(3)可知,试样上所施加的平均载荷取决于应力比的大小,应力比越大,试样上所施加的平均载荷越大。显而易见,更大的平均载荷导致试样更早的由应力强度因子幅度主导的双滑移机制转变为平均载荷主导的拉伸断裂机制。从而使得应力比越大,疲劳裂纹失稳区起始点对应的ΔK值越小,见图3。
从图4(e)中可看出,试样的最终断裂表面呈现为类解理表面,由类似拉伸断口的韧窝形貌转变为类似冲击的解理表面。这归因于,随着平均载荷在裂纹扩展中起主要驱动作用,试样韧带部分越来越小,应力越来越大,裂纹扩展速度愈来愈快,在某一临界ΔK附近,在拉伸载荷下迅速拉断,速度远大于拉伸实验加载速率。它和冲击断裂表面的区别之处在于疲劳裂纹快速断裂区形成的断裂表面解理面具有显著的方向性,解理面沿裂纹扩展方向尺寸更小,且解理台阶显著更高。这是因为在疲劳速断区,尽管拉伸载荷与冲击载荷加载速度都比较快,但受力性质具有明显的不同,疲劳载荷属于张开型载荷,而冲击载荷属于剪开型载荷。
疲劳裂纹扩展门槛值随应力比R的变化趋势如图5所示。从图5可以看出,与疲劳裂纹失稳区起始点对应的ΔK值随应力比的变化趋势相似。随着应力比的增加,裂纹扩展门槛值也呈减小趋势,门槛值和应力比之间具有显著的线性关系,相关系数为0.9969,利用最小二乘法拟合所得公式如下:
ΔKth=9.924(1-0.938R)
(4)
式中:ΔKth为疲劳裂纹扩展门槛值,MPa·m1/2。

图5 应力比R与裂纹扩展门槛值之间关系Fig.5 Relationship between stress ratio R and fatigue crack growth threshold value
式(4)中的9.924MPa·m1/2对应于R=0时的疲劳裂纹扩展门槛值,而式(4)中应力比R前面的系数0.938则决定于材料本身性质。这与文献[16]所呈现公式是一致的,如下式所示:
(5)
式中:ΔKth0为应力比为0对应的门槛值,MPa·m1/2;b为材料常数。
随着应力比增加,材料裂纹扩展门槛值降低,这是由裂纹闭合效应引起的,应力比对裂纹闭合效应的影响较大,文献[17]给出不同材料裂纹闭合效应受应力比影响的相关公式,但大部分都是对于铝合金的研究,对钢的研究则较少。
尽管如此,但本实验结果是很容易理解的,在循环载荷中,只要最小应力Smin小于张开应力Sop时,即Smin 图6为应力比R和裂纹失稳区起始点对应的da/dN之间的关系,相关性也较高,为0.9951。利用最小二乘法拟合的公式如下: (6) 图6 应力比R和裂纹失稳区起始点对应的裂纹扩展速率之间的关系Fig.6 Relationship between stress ratio R and fatigue crack growth rate corresponding to start point of crack unstable zone 从图6中发现,随着应力比增加,裂纹扩展失稳起始点对应的裂纹扩展速度呈下降趋势,这是因为,应力比越大,平均载荷越大,更大的平均载荷更易导致材料在拉伸模式下发生断裂,裂纹扩展失稳起始点对应的裂纹扩展速率没有机会增加到更高程度。 (1)应力比对裂纹失稳区起始点对应的ΔK值具有显著的影响,随着应力比的增加,裂纹扩展失稳区起始点所对应的裂纹扩展速率具有显著的降低。 (2)随着应力比增加,疲劳裂纹扩展门槛值呈现显著的降低趋势,主要归因于裂纹闭合效应。 (3)当疲劳裂纹逐渐由Paris区过渡到失稳扩展区,平均载荷逐渐取代应力强度因子幅度作为裂纹扩展的主导驱动力。 (4)裂纹扩展至拉伸过载区,断口表面呈现明显冲击断裂特征,断裂面具有显著的解理台阶,且解理面具有显著的方向性。 [1] KOTOW K J, PRITCHARD D M. Riserless drilling with casing: Deepwater casing seat optimization [A]. SPE/IADC Drilling Conference, Proceedings[C]. New Orleans: The Society of Petroleum Engineers, 2010.116-129. [2] ROBINSON S D, BEALESSIO T M, SHAFER R S. Casing drilling in the san juan basin to eliminate lost returns in a depleted coal formation [A]. SPE/IADC Drilling Conference, Proceedings[C]. Orlando: The Society of Petroleum Engineers, 2008.406-415. [3] BUNTORO A. Casing drilling technology as the alternative of drilling efficiency [A]. IADC/SPE Asia Pacific Drilling Technology Conference 2008[C]. Jakarta: The Society of Petroleum Engineers, 2008.580-589. [4] KENGA Y, ATEBE J, FEASEY G. Successful implementation of 95/8-in casing drilling in nigeria case history of AKAMBA-2 [A]. The 33rd Annual SPE International Technical Conference and Exhibition[C]. Abuja: The Society of Petroleum Engineers, 2009.1-9. [5] BAILEY G, STRICKLER R D, HANNAHS D, et al. Evaluation of a casing drilling connection subjected to fatigue and combined load testing [A]. The 2006 Offshore Technology Conference[C]. Houston: Sponsor Society Committees of the Offshore Technology Conference, 2006.1-7. [6] ZHAO Z X, GAO D L. Casing strength degradation due to torsion residual stress in casing drilling[J]. Journal of Natural Gas Science and Engineering, 2009, 1(4-5): 154-157. [7] GOKHALE S, ELLIS S. API specification 5CT N-80 grade casing may burst or part unexpectedly if supplementary metallurgical requirements are not specified [A]. SPE/IADC Drilling Conference, Proceedings[C]. Amsterdam: The Society of Petroleum Engineers, 2005.523-528. [8] XU T H, FENG Y R, JIN Z H, et al. Determination of the maximum strain-hardening exponent[J]. Materials Science and Engineering:A, 2012, 550:80-86. [9] 雒设计, 赵康, 王荣. S135钻杆钢的拉扭复合加载疲劳行为[J]. 材料工程, 2013,(1):40-44. LUO She-ji, ZHAO Kang, WANG Rong. Biaxial fatigue behavior under combined axial and torsional loading for S135 drill pipe steel[J]. Journal of Materials Engineering, 2013,(1): 40-44. [10] 沙桂英,韩玉,刘腾,等. 应力幅对退火态Mg-3Al-2Sc合金疲劳行为的影响[J]. 材料工程, 2012,(12): 24-28. SHA Gui-ying, HAN Yu, LIU Teng, et al. Influences of stress amplitude on fatigue behavior of as-annealed Mg-3Al-2Sc alloy[J]. Journal of Materials Engineering, 2012,(12): 24-28. [11] 杨健,董建新,张麦仓,等. 新型镍基粉末高温合金FGH98的高温疲劳裂纹扩展行为研究[J]. 金属学报, 2013, 49(1):71-78. YANG Jian, DONG Jian-xin, ZHANG Mai-cang, et al. High temperature fatigue crack growth behavior of a novel powder metallurgy superalloy FGH98[J]. Acta Metallurgica Sinica, 2013,49(1):71-78. [12] 李松梅,吴凌飞,刘建华,等. 应力比和腐蚀环境对超高强度钢AerMet100 疲劳裂纹扩展的影响[J]. 航空材料学报, 2014,34(3): 74-80. LI Song-mei, WU Ling-fei, LIU Jian-hua, et al. Effect of load ratio and corrosion on fatigue behavior of aermet100 ultrahigh strength steel[J]. Journal of Aeronautical Materials, 2014,34(3): 74-80. [13] LU M X, ZHENG X L. A new microcomputer-aided system for measuring fatigue crack propagation threshold and selecting testing parameters[J]. Engineering Fracture Mechanics, 1993, 45(6):889-896. [14] BOYCE B L, ORITCHIE R. Effect of load ratio and maximum stress intensity on the fatigue threshold in Ti-6Al-4V[J]. Engineering Fracture Mechanics, 2001, 68:129-147. [15] SURESH S. Fatigue of Materials[M]. Cambridge: Cambridge University Press, 1991.202-221. [16] VOSIKOVSKY O. The effect of stress ratio on fatigue crack growth rates in steels[J]. Engineering Fracture Mechanics, 1979, 11(1):595-603. [17] KUMAR R, SINGH K. Influence of stress ratio on fatigue crack growth in mild steel[J]. Engineering Fracture Mechanics, 1995, 50(3):377-384. Influence of Stress Ratio on the Fatigue Crack Propagation Behavior of K55 Casing-drilling Steel XU Tian-han1,WANG Rong1,FENG Yao-rong2,LUO She-ji1, WANG Dang-hui1,YANG Bao1 (1 College of Materials Science and Engineering,Xi’an Shiyou University,Xi’an 710065,China;2 Tubular Goods Research Centre of CNPC,Xi’an 710065,China) The influence of stress ratio on the fatigue crack growth (FCG) behaviour of K55 casing-drilling steel was investigated by means of scanning electron microscopy (SEM) and fatigue tests. The results show that stress ratio possesses a remarkable influence on ΔKresponding to starting point of crack unstable zone. The FCG rates responding to starting point of crack unstable zone exhibit a significant decrease with the increase of stress ratios, and the FCG threshold value possesses a significant decrease. The average load,which is gradually instead of ΔK, turns into the dominant drive force of the FCG when the fatigue crack propagates into the unstable zone from Paris region bit by bit. The fatigue fracture surface exhibits obviously impact facture characterization, when the crack propagates into overload tensile zone. K55 casing-drilling steel;stress ratioR;fatigue crack growth property;stress intensity factor range ΔK;fracture morphology 10.11868/j.issn.1001-4381.2015.06.013 TG142.1+2;TG115.5+7 A 1001-4381(2015)06-0079-06 青年科技创新基金项目(Z12180); 陕西省重点学科专项资金资助项目(YS32030203); 陕西省教育厅自然科学基金(Z12201) 2014-01-24; 2014-11-15 许天旱(1971-),男,博士,副教授,主要从事材料力学性能与表征的研究,联系地址:陕西省西安市电子二路18号西安石油大学材料科学与工程学院(710065),E-mail:xutianhan@xsyu.edu.cn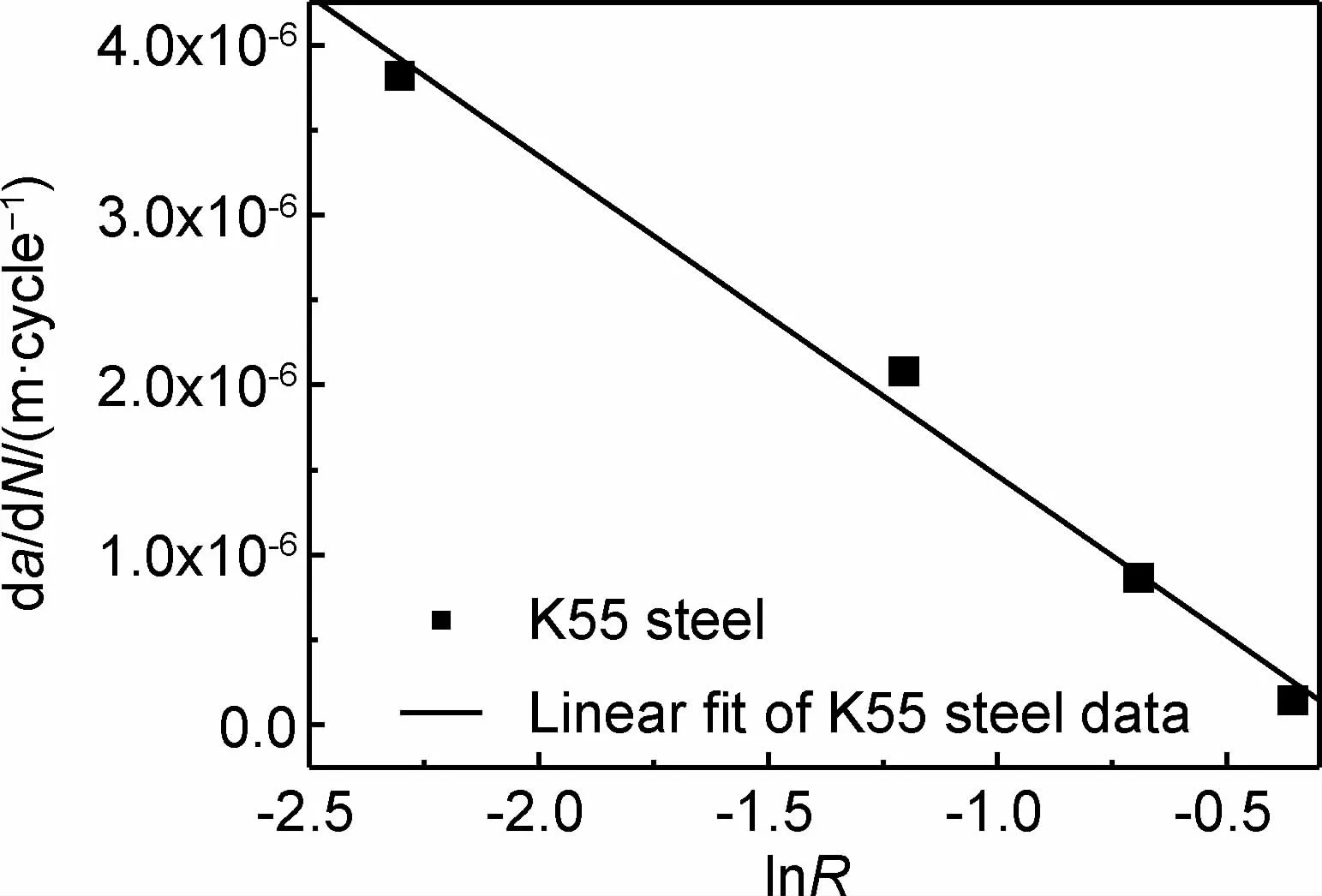
3 结论
