孔道弯曲情况下锚索锚固段力学特性分析

索玉文 朱宝龙 郭华伟 牛小玲 赵什光 于 贵

(1.西南科技大学土木工程与建筑学院 四川绵阳 621010 ；2.中铁西北科学研究院有限公司 甘肃兰州 730000)



孔道弯曲情况下锚索锚固段力学特性分析

索玉文1朱宝龙1郭华伟1牛小玲1赵什光1于 贵2

(1.西南科技大学土木工程与建筑学院 四川绵阳 621010 ；2.中铁西北科学研究院有限公司 甘肃兰州 730000)

工程案例表明，锚索孔道存在一定的弯曲，较多关于锚索的受力分析将锚索简化成是直的，并不能反映实际受力情况。以半平面弹性理论为基础，结合数学计算方法，建立了包含弯曲半径在内的锚固段受力模型，利用弹性理论推导出锚固段在弯曲情况下剪应力关于锚固段长的计算公式，并通过算例给出了锚固段弯曲情况下内、外两侧曲线上的剪应力分布图。与直线情况下剪应力分布图进行比较，分布情况更为合理。

预应力锚索 弯曲 弹性理论 剪应力分布

近20年来，随着三峡工程、葛洲坝等大型水电工程的竣工，大量的锚索锚固工程应用其中。现在预应力锚索锚固技术已成为一种无可替代的岩土工程安全加固措施。所以对于岩土锚索锚固理论的研究显得至关重要。就此问题国内外已有一定研究，但是在其设计理论和受力计算方法上仍不够完善。在锚固工程实际施工时，由于钻具的结构和尺寸的不合理或者在钻孔过程中遇到倾斜或软弱交替的岩层时都会发生钻孔弯曲的情况[1-2]。因为地质因素是客观存在的，现有的钻孔技术和施工工艺水平又有限，所以锚索发生弯曲情况是无法避免的。而很多关于锚索锚固段受力分析把锚索锚固段的受力模型简化成轴对称的圆柱体，虽然计算简便但却并不符合实际情况。

对于锚索锚固段周边剪应力分布规律的研究已有一定的成果，如：Phillips[3]对于拉力型锚索进行了研究，发现锚索表面剪应力沿锚固长度上的分布呈指数关系，并推导出了相应的计算公式；张端良等通过弹性理论分析方法，对锚固段周边剪应力进行分析求解，模拟求出剪应力沿锚固段轴向的分布曲线[4]；何思明等将岩体剪切损伤理论与常规剪切位移法相结合，研究了拉力型预应力锚索锚固段的荷载-位移特性、侧阻力分布特性以及轴力分布特性[5]；蒋良潍等基于弹性半无限空间的 Mindlin 位移解推求锚固段侧阻力分布，发现Mindlin 位移解所具有的数学奇异性影响突出，提出传统的剪应力互等定律在局部区域不完全适用的结论[6]；文献[7-10]也对该问题进行了相关的研究并得出了一定的结论。

以上学者大都是对锚索直线情况下锚固段受力情况进行分析，对于弯曲情况下鲜有涉及。本文结合弹性力学的相关理论和数学计算方法，对锚索弯曲情况下锚固段周围的剪应力分布规律进行分析。

2 锚固段受力机理

锚索在受力过程中，首先将预拉应力P作用在锚索的自由段，随后由自由段传递给锚固段。最终锚固段内的锚索体与浇筑的浆体作为一个整体来对周围的岩体施加一个紧固力。根据锚索锚固段的受力原理，本文假设了锚固段弯曲时的受力情况。为计算简便，忽略掉预应拉力在自由段的损失值和锚固段周边土体对锚固段施加的竖向及横向力。取锚索弯曲方向所在的平面，只讨论该平面上最外侧曲线上的剪应力分布情况。锚固段受力情况示意图如图1。

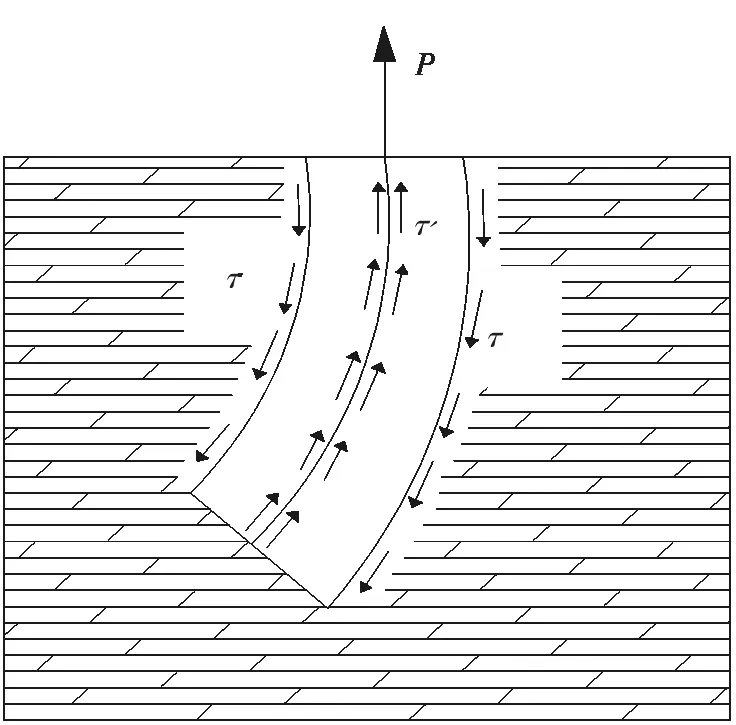
图1 锚固段受力情况Fig. 1 The forces anchoring segment

此处只讨论了锚固段弯曲的一种情况，对于锚固段的其他弯曲情况可用类似的方法来进行研究和分析。

3 锚固段力学模型建立

根据弹性力学[11]半平面理论，半平面体任意点处应力如图2所示，假设y轴以下为半平面体，边界上受集中力P作用，并且与边界法线成角β，与法线成任意角φ，且与点O距离为ρ处的点的应力用σρ和τρφ来表示。同理，按照上述方式来建立锚固段力学模型。如图3所示。

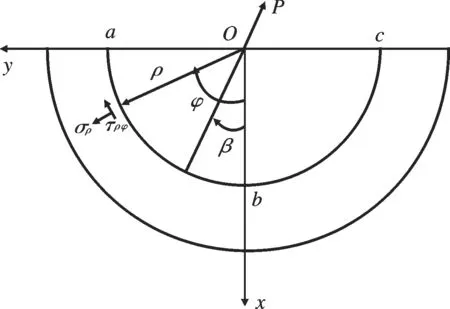
图2 半平面体任意点处应力 Fig.2 Any point in vivo half-plane stress

图3 锚固段力学模型Fig. 3 Anchorage segment mechanical model components in polar coordinates

由图3可以看出，假设锚固段的弯曲半径为R，锚固段的直径为D，预拉应力P与边界法线的夹角β=0。锚固段弯曲弧段所对应的圆心角设为角θ。根据半平面弹性理论，把相容方程、边界条件以及平衡方程联立可得半平面上任意一点处的应力分量的值，即

(1)

σφ=0

(2)

τρφ=τφρ=0

(3)

当β=0时，应力分量可表示为

(4)

σφ=0

(5)

τρφ=τφρ=0

(6)

对于锚固段力学分析模型而言，为适用上述公式，在此将其分成内侧曲线和外侧曲线两部分来进行计算。首先讨论锚固段内侧曲线上的剪应力分布规律。将内曲线上应力和角度的关系由图4表示出来。图中Q点为弯曲圆点，弧段AB表示锚固段内侧曲线，弧段GH表示锚固体，弧段CD表示锚固段外侧曲线。E点为内侧曲线上任意一点，直线FE为弧段AB上过点E的切线，弧段AE的弧长用s1表示，弧段AE对应的角度用θ'来表示，点E处的应力分量分别为σρ和τρφ，τ为锚固段内侧曲线在任意点E处沿弧段AB的切线方向的剪应力，它可由σρ和τρφ合成得到。

图5为锚固段内侧曲线任意一点E处的应力角度关系图。图中设σρ与τ的夹角为γ，坐标轴原点G距任意点E的距离为ρ，GE与x轴的夹角为φ。

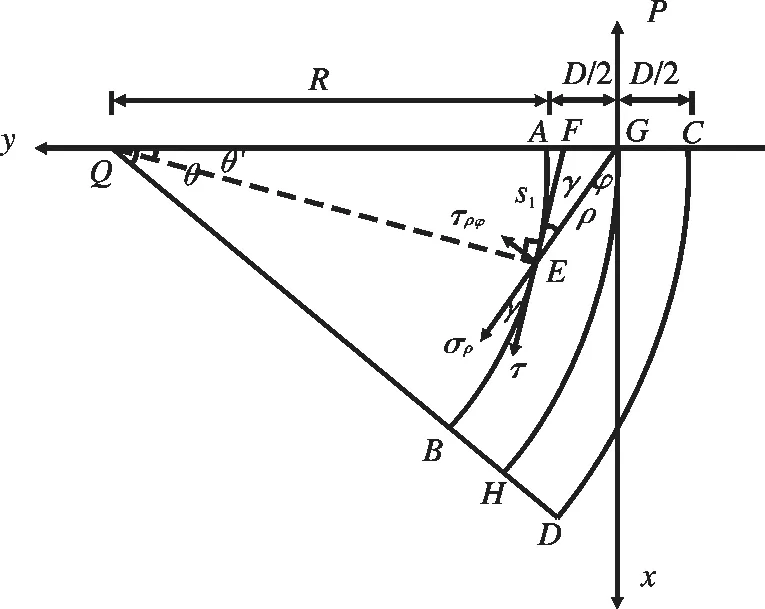
图4 锚固段内侧曲线上任意点处应力分量Fig. 4 Stress components at any point on the inside of the curve anchoring segment

图5 任意点E处应力角度关系图Fig. 5 E angle at any point in the relationship between stress map

根据三角形QEG的内角关系可以得到

(7)

即

γ=φ-θ′

(8)

根据弧长公式得到

(9)

根据余弦定理可知

(10)

根据正弦定理可知

(11)

即

(12)

(13)

同理，锚固段弯曲情况下外侧曲线上剪应力τ与应力分量σρ和τρφ的关系由图6给出。图中点K为外侧曲线上任意一点，直线LK为弧段CD上过点K的切线，弧段CK的弧长用s2表示，弧段CK对应的角度用θ'来表示，点K处的应力分量分别为σρ和τρφ来表示，τ为锚固段内侧曲线在任意点K处沿弧段CD的切线方向的剪应力，它可由σρ和τρφ合成得到。

图7为锚固段外侧曲线任意一点K处的应力角度关系图。图中设σρ与τ的夹角为γ，坐标轴原点G距任意点K的距离为ρ，GK与x轴的夹角为φ。

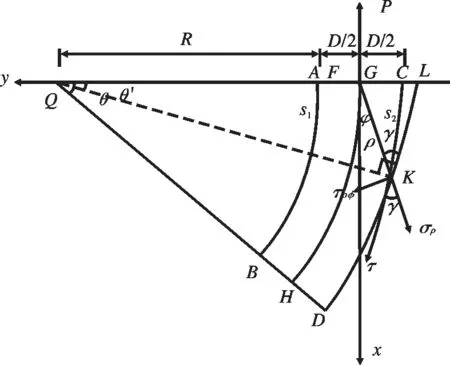
图6 锚固段内侧曲线上任意点处应力分量 Fig. 6 Stress components at any point on the inside of the curve anchoring segment

图7 任意点K处应力角度关系图Fig. 7 K angle at any point in the relationship between stress map

根据三角形内角关系可以得到

(14)

即

γ=φ+θ′

(15)

根据弧长公式得到

(16)

(17)

根据正弦定理可知

(18)

即

(19)

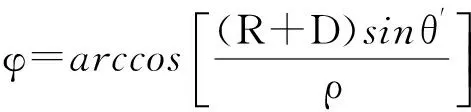
(20)

由图5及图7中可以看出剪应力τ与应力分量σρ和τρφ的关系为

τ=σρcosγ+τρφsinγ

(21)

将式(4)、式(5)、式(6)代入式(21)得

(22)

将式(8)-式(10)及(13)代入式(22)中可以得到锚固段弯曲情况下内侧曲线上剪应力分布规律，将式(15)-式(17)及(20)代入式(22)中可以得到锚固段弯曲情况下外侧曲线上剪应力分布规律。

4 实例分析

某市欲建造一大厦，在基坑开挖时采用拉力型锚索进行加固。锚索用的是高强、低松弛的预应力钢绞线，预应力钢绞线弹性模量为E=200 GPa，泊松比为 0.15。锚索锚固段长为 6.0 m。锚索设计预应力值为1 000 kN，锚索钻孔直径为 140 mm，采用水泥砂浆浇注。由于地质软硬程度不同，锚孔在钻制过程中极易发生弯曲，测得锚固段曲率半径为20 m。图8为应用本文推导的计算方法，选取有效参数对预应力锚索分级加载600 kN，800 kN及1 000 kN时，锚固段内外侧曲线剪应力分布规律图。

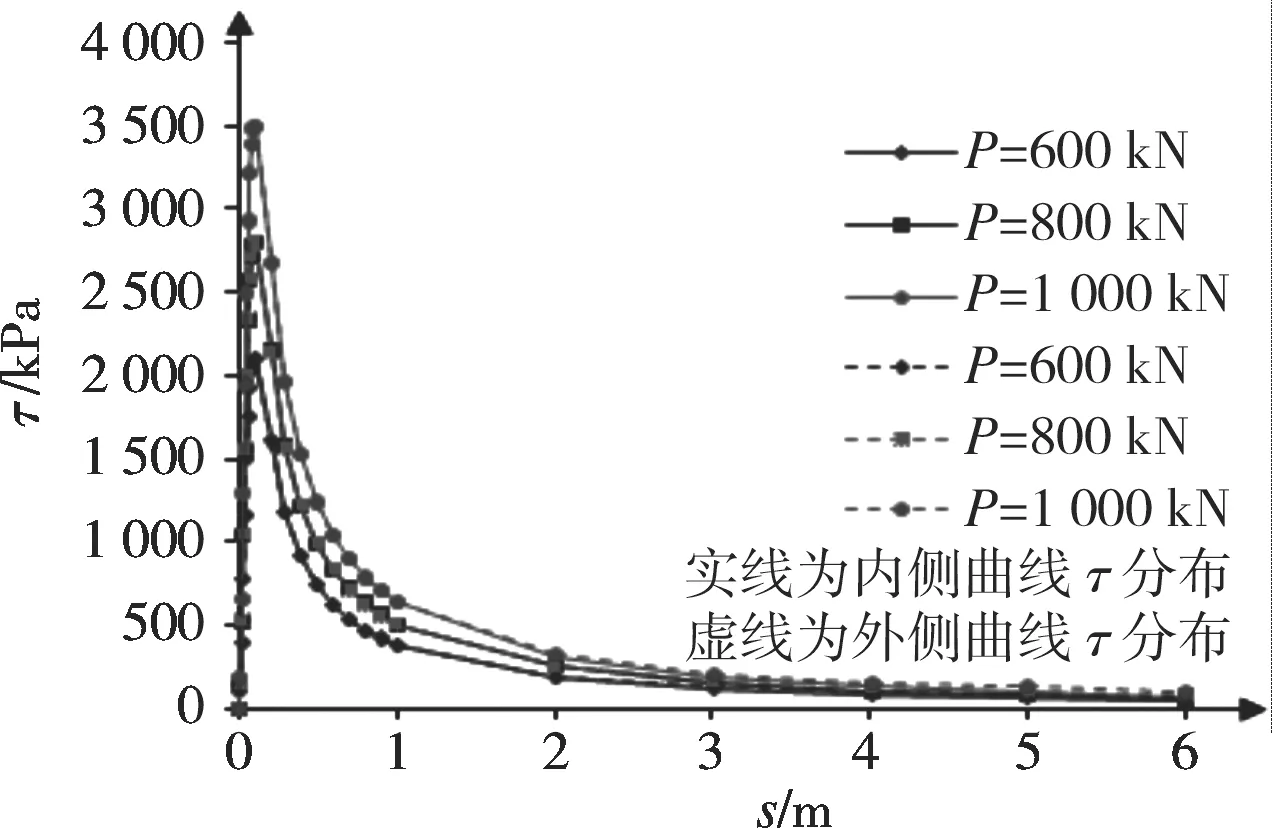
图8 孔道弯曲情况下锚索弯曲平面内外侧曲线上的剪应力分布图Fig. 8 Within anchor outside of shear stress distribution under bending conditions

从图8可以看出，锚索在孔道弯曲情况下锚固段周边剪应力沿弯曲平面内外侧曲线的剪应力分布基本相同，即剪应力沿锚固段从零开始，快速增大，在弧段长为0.1 m时增大至剪应力峰值后逐渐减小，直至锚固段末端趋于平缓接近零但并未为零。

4.1 孔道弯曲与直线情况下剪应力分布对比分析

为研究孔道弯曲情况下锚固段剪应力分布的规律，将其与直线情况下剪应力分布规律进行对比分析。由文献[3]可知轴对称情况下锚索锚固段周边剪应力分布规律可用下式表示：

(23)

将算例中的参数代入式(23)中，可以得出理想的直线锚固段周边剪应力分布规律，将直线和弯曲两种情况下剪应力分布规律进行对比(图9)。

如图9所示，孔道弯曲与直线情况下锚固段剪应力分布规律大致相同，但是曲线情况下剪应力峰值比相同拉力P作用时的直线情况下剪应力峰值要大，且随着拉力P的增大，峰值差值也会随之增大。

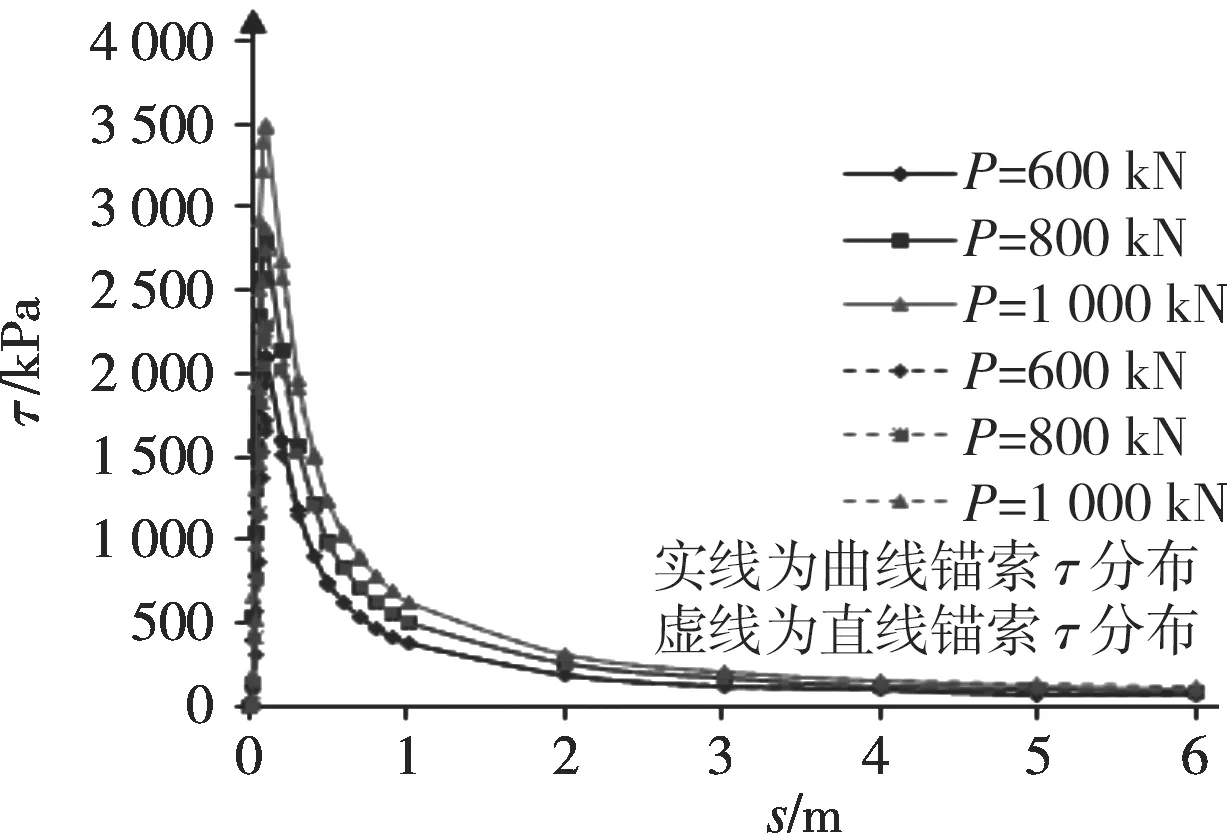
图9 孔道直线和曲线情况下锚索锚固段剪应力分布规律对比图Fig. 9 Comparison of shear stress distribution under the curve and the straight line case

为进一步明确孔道弯曲对剪应力分布的影响，下面引入剪应力差值Δτ，即相同条件下锚固段曲线情况下的剪应力与直线情况下的剪应力的差值。

Δτ=τ曲线-τ直线

(24)

由图10可以看出，与剪应力分布规律不同，剪应力差值Δτ仅在0～0.3 m范围内有明显的变化，变化规律为由零开始迅速增大，且在0.05 m处达到峰值，然后逐渐减小，在0.3 m处减小为零。且剪应力差值Δτ的峰值同施加的拉力P的大小基本一致。由于剪应力差值Δτ大于零的区域恰好是锚索锚固段剪应力分布集中部位，即锚固段最容易发生断裂的地方，因此孔道弯曲的存在会加大锚索锚固段的受力集中、加速锚固失效。

图10 孔道曲线和直线情况下锚索锚固段剪应力差值分布规律Fig. 10 The difference of shear stress distribution between the curve and the straight line case

4.2 不同曲率半径对剪应力分布的影响分析

锚索曲率半径的大小是影响孔道弯曲情况下剪应力分布规律的重要因素之一。在算例参数的基础上，分别考虑曲率半径为R=5 m，R=10 m，R=20 m，R=200 m和R=2 000 m，拉力P=1 000 kN时锚固段周边剪应力的分布形式。通过计算可知不同曲率半径的锚索剪应力分布仅在锚固段0～0.3 m范围内差异较为明显，因此只考虑该段内剪应力分布规律。如图11所示。

图11 不同曲率半径情况下锚索锚固段剪应力分布规律Fig. 11 Anchorage shear stress distribution under different radii of curvature segment case

曲率半径的大小决定锚索锚固段的弯曲程度，曲率半径越小，锚固段弯曲弧度越大，曲率半径越大则相反。如图11所示，随着曲率半径的增大即弯曲弧度的减小，剪应力峰值逐渐减小。按照此规律推算，曲率半径增大至无穷时的剪应力分布曲线必定会与直线情况下剪应力分布曲线重合。

5 结论

通过弹性理论对弯曲情况下锚索周边剪应力分布规律的分析可以看出：(1)弯曲情况下锚索锚固段周边剪应力分布规律与直线情况下周边剪应力分布规律基本一致，都是从零开始，短距离内增大至峰值，然后减小，直至平缓，但并不为零。相同拉力P作用时，弯曲情况下锚索锚固的剪应力峰值比直线情况下大，且随着拉力的增大而增大。(2)由于剪应力差值Δτ大于零的区域恰好是锚索锚固段剪应力分布集中段，因此孔道弯曲的存在加大了锚固段应力集中，且加速了锚固失效。(3)锚索锚固段曲率半径的大小影响锚固段周边剪应力的分布。曲率半径越小，剪应力分布的峰值越大，应力集中越明显，对锚固体材料的强度性能要求越高，对锚索加固越不利。(4)本文通过对孔道弯曲情况下锚索锚固段受力理论解的推导，对于分析锚索锚固段弯曲时的力学特性及影响因素有重要意义。

[1] 黄辉,牟文俊,陶林.浅析大吨位、超长孔深锚索钻孔孔斜控制[J].探矿工程(岩土钻掘工程), 2010, 37(6): 71-74.

[2] 赵廷严.浅析钻孔弯曲产生的原因及预防纠正措施[J].中国煤炭地质,2009,21(1):62-63.

[3] STILLBORG B. Experimental Investigation of Steel Cables for Rock Reinforcement in Hard Rock [ D].Sweden: Lulea University of Technology, 1984.

[4] 张端良,董燕军,唐乐人,等.预应力锚索锚固段周边剪应力分布特性的弹性理论分析[J].岩石力学与工程学报,2004,23(S2):4735-4738.

[5] 何思明,王成华, 吴文华. 基于损伤理论的预应力锚索荷载变位特性分析[J]. 岩石力学与工程学报,2004, 23(5): 786-792.

[6] 蒋良潍,黄润秋.Mindlin 位移解推求锚固段侧阻力分布方法中的奇异性问题[J].岩土工程学报,2006,28(9):1112-1117.

[7] 张四平,侯庆.压力分散型锚杆剪力分布与现场试验研究[J].重庆建筑大学学报,2004,26( 2) : 41 -47.

[8] 张季如,唐保付. 锚杆荷载传递机理分析的双曲函数模型[J].岩土工程学报,2002,24( 2) : 188 - 192.

[9] 尤春安, 战玉宝. 预应力锚索锚固段界面滑移的细观力学分析[J]. 岩石力学与工程学报, 2009, 28(10): 1976-1985.

[10] LUTZ L, GERGELEY P. Mechanics of band and slip of deformed bars in concrete[J]. Journal of American Concrete Institute.1967, 64 (11): 711-721.

[11] 徐芝纶.弹性力学,第三版[M].北京:人民教育出版社,2002.

Mechanical Properties Analysis of Anchorage in the Case of Channel Bend

SUO Yu-wen1， ZHU Bao-long1， GUO Hua-wei1， NIU Xiao-ling1，ZHAO Shi-guang1， YU Gui2

(1.SchoolofCivilEngineeringandArchitecture,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan,China；2.NorthwestResearchInstituteCo.,Ltd.ofC.R.E.C,Lanzhou730000,Gansu,China)

This project actually show that there is certain bent, in the process of making prestressed cable hole, while most analysis on the shear stress around the anchoring segment depicts anchoring segment as straight, and therefore can not reflect the actual situation by force. Based on the half-plane elasticity theory, combining mathematical calculation, anchoring segment contains the bending radius force, including the model, was established. Using elastic theory formulas of the lengh of anchoring section at bending shear stress on the anchorage section was deduced and numerical examples were given in the next section of the curved anchoring case and the shear stress distribution on the inner and outer sides of the curve were given. This distribution is more reasonable compared with linear circumstances under shear stress distribution.

Prestressed cable; Bending; Elasticity theory; Hear stress

2014-12-24

中国中铁股份有限公司重点项目(2014-重点-76)。

索玉文(1990—)，女，硕士研究生，研究方向为岩土工程。Email：1132640108@qq.com

TU311

A

1671-8755(2015)02-0055-06