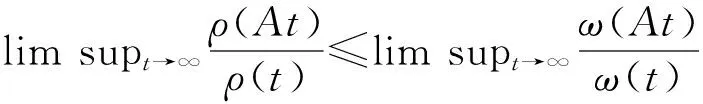ω-超广义函数中加权函数的一些性质
2015-03-03陈丫丫
陈丫丫
(太原学院 数学系,山西 太原 030001)
ω-超广义函数中加权函数的一些性质
陈丫丫
(太原学院 数学系,山西 太原 030001)
讨论构造ω-超可微函数和ω-超广义函数的伪解析和非-伪解析两类加权函数的一些性质,给出了加权函数的一个存在条件.
加权函数;Young共轭;伪解析和非-伪解析

在ω-超可微函数和ω-超广义函数的研究中,加权函数的结构和性质起着非常重要的作用.本文通过对于伪解析和非-伪解析两类加权函数的讨论,给出了它们的一个存在性条件.这些结果可以被用于ω-超可微函数和ω-超广义函数的研究中.
我们先给出本文所涉及到的一些基本概念和记号:
定义1 1)设ω是[0,∞)→[0,∞)上的连续的单增偶函数,如果满足:
(H1)存在正数K,使得对于所有的t≥0,有ω(2t)≤K(1+ω(t));
(H3)ω(t)=Ο(t),t→∞;
(H4)φ:[0,∞)→[0,∞),φ(t)=ω(et)为凸函数,

2)设ω为一加权函数,如果ω满足
则称ω是伪解析的.否则,称之为非-伪解析的.

称之为φ的Young共轭为.
例1 下面的函数都是加权函数:
1)ω(t)=tα,0<α≤1.
2)ω(t)=(log(1+t))β,β>1.
3)ω(t)=t(log(1+t))-β,β>0.
4)ω(t)=|t|.
其中1)当0<α≤1,3)当β>1时和2)是非伪解析的;3)当0<β<1时和4)是伪解析的加权函数.
例2 1)设ω1=max(t-1,0),t∈[0,∞),则ω1是一个伪解析的加权函数.因为φ1(x)=ω1(ex)=ex-1,x≥0,可得
我们已经知道,对于每个开集Ω⊂Rn,ω-超可微函数空间ε{ω1}(Ω)E}与实解析函数空间Α(Ω)也是拓扑同构的,而ε{ω1}(Ω)与整函数空间H(Cn)是拓扑同构的[7].

注 在下面的讨论中,只要不特别注明,则结论对于伪解析和非-伪解析两类加权函数都是成立的.
接下来,我们来讨论加权函数的性质:
引理1 对于上面定义1中的加权函数φ,容易验证下列命题成立:
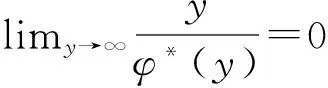
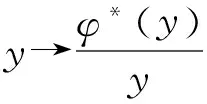
3)φ*(λx)≤λφ*(x),0≤λ≤1,x≥0.
引理2 设ω是一个加权函数,那么:
证明 根据ω加权函数的定义,我们有:


引理3 设φ是定义1(δ)中所定义的函数,那么,对其Young共轭φ*有
证明 首先,根据φ的定义和加权函数ω的性质(α),可知存在L>1,使得:

由此
引理4 设ω是加权函数,φ(x)由定义1(δ)所定义,K为(α)中所给,那么有:
1)φ(x+j)≤2jK2j(1+φ(x)),x≥0,j∈N;
2)对于每个k,l,m∈N,∃μ∈N,C>0,使得:
3)对于每个k,l,m∈N,∃μ∈N,C>0,使得:
证明
1)由定义2.1中的(α)以及φ的定义可得:
由此可以得出:
2)若k,l,m给定,由(1)可取K′,使得
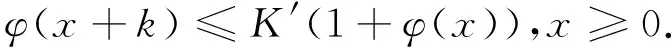
由此可取μ∈N,使得μ≥2K′m,使对x≥k有:
所以

3)取充分大的μ,μ≥m,利用与(2)同样的方法即可证得(3).
引理5 1)对任意的加权函数ω,存在常数L>0使得
其中ω1(t)由例2所给.由Young共轭定义可得
2)如果ω=ο(t),那么对于每个l∈N,存在常数Cl>0,使得
下面,我们来给出加权函数的一个存在性条件:
1、优化财政支农结构,明确支农资金重点投入领域。在确保粮食安全的基础上,财政支农资金重点向科技创新、产业融合、品牌营销、农业转型升级和绿色发展、农村电商等农商文旅融合的新产业新业态领域投入,以着力补齐农村农业发展短板,加快促进广西农业供给侧结构性改革,激发农业农村发展内生动力。
定理 设ω是加权函数.如果g:[0,∞)→[0,∞),满足g(t)=ο(ω(t))(t→∞),那么,必然存在加权函数σ,满足:
1)g(t)=ο(σ(t)),(t→∞);
2)σ(t)=ο(ω(t)),(t→∞);
如果存在R≥1,使得ω|[R,∞)是凹的,则σ|[R,∞)也是凹的.
证明 首先我们证明以下结论成立:如果ω|[R,∞)是凹的,则ω∈C′(R,∞).

另一方面,因为φ(x)=ω(ex)是凸的,因此有
所以,ω,φ是可微的,并且由导数的单调性,ω′(t)还是连续的.
对于一般情形,假若ω∉C1.那么,我们可取一个C1-函数χ≥0使之满足Suppχ⊂(0,log2),并且∫χ=1.我们定义
于是,对于定义(2.1)(α)中的常数K,因为:
所以有φ(x)≤ψ≤K(1+φ(x)).
因为
和
以及
和
所以有
即ρ满足定义2.1(β)和(γ).
又∀x1,x2∈[0,1],λ+μ=1
所以,ψ(t)=ρ(et)是凸的.即ρ满足定义1(δ).
设A,B>1,对充分大的t,有ω(At) 所以,ρ(At)=ψ(a+logt)≤Bψ(logt)=Bρ(t).既ρ满足定义1(α)且 至此,我们可以假设对某个R有ω|[R,∞)∈C1.另外,还可以假设log(1+t)=ο(g(t)).注意到φ(0)=0,设x1=y1=z1=0,我们定义递推序列{xn},{yn},{zn},使得x2>R, (1) (2) (3) (4) (5) 可以证明 (6) 由(5)和(4)可以得到 因为φ′单增,所以上式非负.另一方面,由(5)可得: 现在,我们定义ψ 由(4),(5)可知ψ∈C1,又由定义可见ψ还是凸的.下面,我们定义σ为 σ(t)=ψ(max(logt,0)).显然,σ∈C1, 此外,当ω为凹函数时,由ψ的凸性,可知σ也是凹的. 下面,我们来证明σ即为所求. 首先,我们证明 (7) 对于x∈[yn,xn+1],(7)显然成立.对于x∈[xn,yn],由(4)以及φ的凸性可得 由(2)和估计式(7)即得结论(1):g(t)=ο(σ(t)). 为了证明(2):σ(t)=ο(ω(t)),我们先来考虑yn≤x≤xn+1的情况.由(3),(6)可得 接下来考虑xn≤x≤yn.依据φ的凸性,得到 因此,当t→∞时,有ψ=ο(φ),从而σ(t)=ο(ω(t)),(2)得证. 为了证明(3),对给定的A>1,设a=logA,下面来估计ψ(x+a)-ψ(x): 对于[x,x+a],有以下五种情形 我们只需要考虑其中的两种即可,其它情形皆类似. 情形一:xn≤x≤yn 再由(7)式即得 情形二:xn≤x 由此,对上述的σ,由(3)可推得其满足定义1(α),由(2)可推出其满足(γ),由(1)可推得其满足(β),证毕. [1] A.Beurling.Quasi-analyticaity and General Distributions[M].Stanford:AMS Summer Institute,1961 [2] G.Bjock.Linear partial dierential operators and generalized distributions[J].Ark.Math,1965(6):351-407 [3] R.W.Braun,R.Meise,B.A.Taylor.Ultradierentiable functions and Fourier analysis[J].Resulte Math,1990(17):206-237 [4] J.Bonet,R.W.Braun,R.Meise,B.A.Taylor.Whitney’s extension theorem for nonquasianalytic classes ofultradierentiable functions[J].Studia Math,1991,99(2):155-184 [5] J.Bonet,R.Meise.Ultradistributions of Roumieu type and projective descriptions[J].Math.Anal.and Appl,2001(255):122-136 [6] J.Bonet,R.Meise.Quasianalytic functionals and projective descriptions[J].Math.Scand,2004,94:249-266 [7] Heinrich T,Meise R.A support theorem for Quasianalytic functionals[J].Math.Nachr,2007(28):364-387 [8] Bonet J,Meise R.On the theorem of Borel for quasianalytic classes[J].Math Scand,2013,112(2):302-319 Some Properties of Weight functions in ω-Ultra-distributions Chen Yaya (Department of Mathematics,Taiyuan College, Taiyuan 030001, China) The properties of weight functions of quasianalitic and non-quasianalitic typeinω-ultra-distributions andω-ultra-differentiable functions are discussed, and one exestence condition for weight function is geiven. weight function;Young conjugate;quasianalitic and non-quasianalitic 2015-01-15 山西省回国留学人员科研资助项目(2012-011). 陈丫丫(1982-),女,山西阳泉人,硕士,太原学院讲师.主要从事泛函分析研究. 1672-2027(2015)02-0011-06 O177 A