一类含特殊项的非线性阻尼的Sine-Gordon梁方程的弱解

段振兴,郭尊光

(太原工业学院 理学系,山西 太原 030008)

一类含特殊项的非线性阻尼的Sine-Gordon梁方程的弱解

段振兴,郭尊光

(太原工业学院 理学系,山西 太原 030008)

文章对动力系统中的一类含特殊阻尼项的非线性Sine-Gordon型方程的弱解进行了证明,方程在一定的空间下满足一定的初边条件,所采用的方法是Galerkin法．

非线性;Galerkin法；弱解

0 引言

文研究了一类非线性阻尼的Sine-Gordon型方程的弱解,文研究了新三维系统对应的分段型和指数型混沌系统,文[3-4]研究了非线性弹性杆方程的初边值问题和梁方程的渐近解,都是利用了Galerkin方法．

本文方程:

(1)

在初始条件:

及边界条件(a):

下弱解的存在性．

1 函数空间

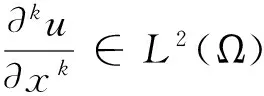
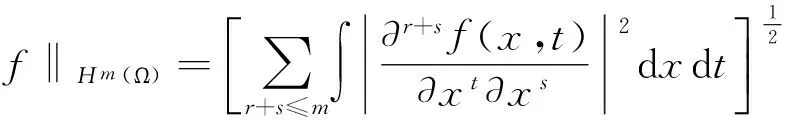
2 假设

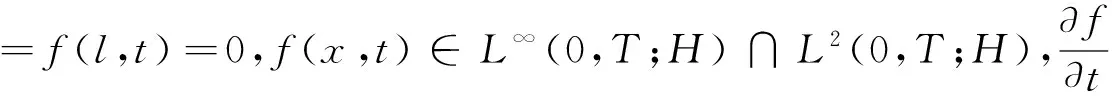
对于函数g(s)满足:g(0)=0,g(s)=c2(R);g(s)≤c(1+|s|3);g′(s)≤c(1+|s|2)

3 定理及证明

定理1 若函数f(x,t),g(s)满足上述条件,u0∈s3∩c1(Ω),u1∈H1(Ω),则方程(1)在边界条件(a)下存在局部弱解u≡u(x,t),其中

对于∀ωj∈wm满足:

(2)

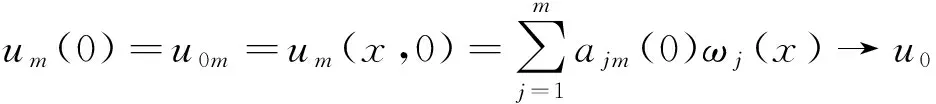
则此方法相当于把偏微分方程问题转化为关于ajm(t)的常微分方程组的柯西问题,由皮亚诺定理知,只要tm>0,在[0,tm]中一定存在唯一的实解ajm(t),即存在唯一的解um(x,t).

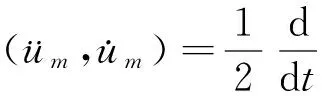
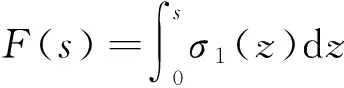
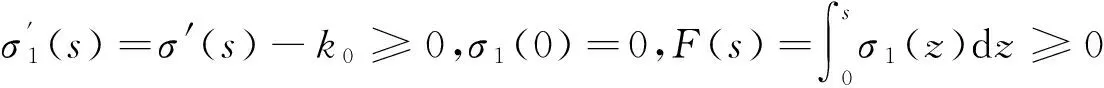
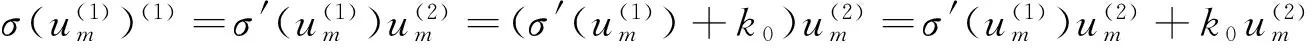
方程(2)写成

(3)

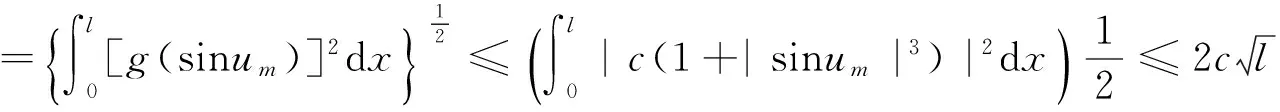
即

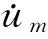
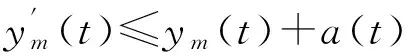
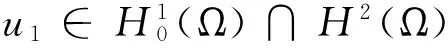
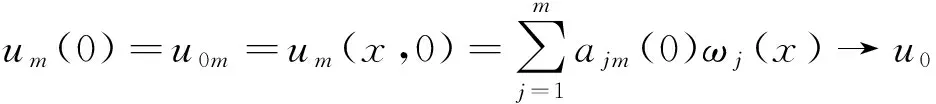
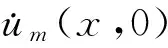
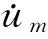
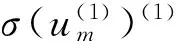
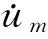
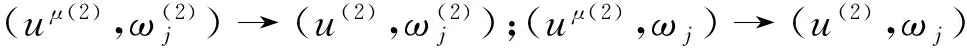
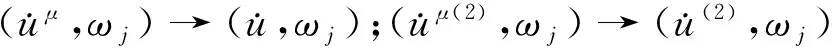
(4)

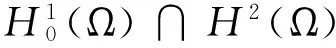
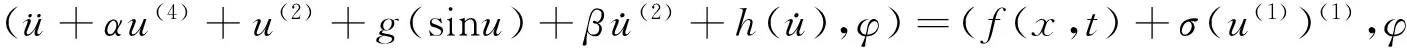
[1] 段振兴,张建文,具非线性阻尼的Sine-Gordon型方程的弱解[J].太原理工大学学报,2008,s2:101-103

[2] 张玲梅.一个新三维系统对应的分段型和指数型混沌系统的研究[J].太原理工大学学报,2015,2:238-24

[3] 牛丽芳.一个具有黏阻尼的非线性弹性杆方程的初边值问题[J].太原理工大学学报,2014,1:128-132

[4] 任永华.非自治强阻尼梁方程的渐近行为[J].太原理工大学学报,2013,1:16-118

[5] LIKHAREV K K.Introduction to the dynamics of josephson junction[M].Russian:Nauka,Moscow,1985

Weak Solutions for a Kind of Nonlinear Sine-Gordon Equation with Damping and Special Item

DUAN Zhenxing, GUO Zunguang

(Department of Science, Taiyuan Institute of Technology,Taiyuan 030008, China)

We study the thesis about some research on a kind of nonlinear and damp Sine-Gordon equation of the physics and give the proof of existence and uniqueness under a certain initial boundary conditions and a certain space by Galerkin method.

nonlinear;Galerkin method;weak solutions

2015-11-10

段振兴(1982-)，男，山西忻州人，硕士，太原工业学院理学系助教，主要从事偏微分方程研究.

1672-2027(2015)04-0014-04

O175.29

A