精密轨道定位方法的改进
2015-03-03唐颖哲冯来平欧阳明达
任 锴,唐颖哲,冯来平,欧阳明达
精密轨道定位方法的改进
任 锴1,2,唐颖哲3,冯来平3,欧阳明达1,2
( 1.信息工程大学地理空间信息学院,河南郑州450052; 2.西安测绘信息技术总站,陕西西安710054; 3.西安测绘研究所,陕西西安710054)
一、引言
文献[1]在GPS动态定位应用中,推导了一种利用多参考站和高精度轨道,采用非差观测值,同步计算测站位置和卫星钟差的定位方法,且将此方法命名为精密轨道定位( precise orbits positioning,POP)方法。对距基站数百千米至上千千米长度的流动站,比较了该方法与PPP( precise point positioning)方法的计算结果,结果表明在收敛速度、测站精度方面,该方法都有一定优势。
本文对该方法进行了分析,在两个方面进行了扩展:一是通过对静态测站数据处理,将对高精度轨道的要求进行了扩展,计算表明,完全可以采用广播星历;二是对包括基站同步处理的非差观测数据进行整周模糊度约束,将结果由模糊度实数解扩展到固定解。采用IGS网站数据进行了计算,结果表明,本文在这两方面的扩展是合理的,方法具有一定参考价值。
二、POP原理
PPP解算需要高精度的卫星轨道和钟差产品[2],在实时应用中,高精度的轨道可以通过预报得到。如IGS的超快速轨道产品,它就是通过24 h的实测数据定轨并外推24 h,提供48 h轨道产品,每6 h更新一次,超快速轨道产品预报轨道的精度可以达到5 cm[3]。而预报卫星高精度钟差产品是比较困难的,原因是卫星钟噪声影响难以建模,因此,在没有高精度卫星钟差的情况下,无法进行基于非差方法的PPP解算。
文献[1]利用多个位置已知的基站,采用高精度轨道产品,仍采用非差观测数据,同步估计卫星钟差和流动站位置,以达到流动站高精度定位的目的。由于所有卫星钟差和接收机钟差设为未知参数时,将使法方程病态,因此只能计算相对钟差。即将其中的一个基站接收机钟差固定,该站称为主站,因此在该方法中,数据处理包括主站、基站和待定站。
观测值采用无电离层影响的伪距和载波相位组合,主站0观测卫星j的观测方程为

式中,左侧分别为伪距和相位的观测值减计算值,计算值的各项改正处理除卫星钟差外与PPP方法相同; ztd0为对流层天顶延迟参数; wmapj0为湿延迟映射函数值; dtj为卫星钟差; c为真空中光速; BCj0为初始模糊度参数。
基站i观测卫星j的观测方程为
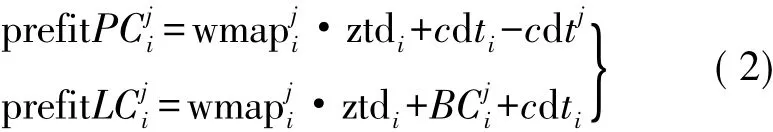
式中,dti为接收机钟差;其余量含义同主站,只是对应于基站i。
待定站r观测卫星j的观测方程为

式中,( dx,dy,dz)为测站位置参数(相对于初始值的改正值) ; ( l,m,n)为测站到卫星的方向余弦;其余量定义同前,对应为测站r。
对上述3组方程分析可见,虽采用的是非差观测值,但通过卫星钟差这个参数,将3组方程联系到一起。文献[1]认为可相似于组差。
既然可相似于组差,那么组差主要在高精度相对定位中应用,在相对定位中,尤其是中短距离的基线解中,轨道精度影响有限,广播星历计算的轨道即可满足高精度的基线解算。因此,可以将POP方法扩展到利用广播星历进行处理,本文算例支持了这种扩展。
由于有同步处理的主站和基站观测值,因此,在事后处理中,在得到高精度的非差模糊度实数解之后,可以进一步利用多站同步观测值,构建双差观测值,利用双差模糊度的整数特性,构建对原始非差模糊度的约束值,从而利用这种约束值得到非差模糊度固定解。这是本文对POP方法的第二处扩展。
三、非差模糊度固定原理
对主站、基站、待定站组成的测站网,本文采用的非差模糊度固定解算法,有的文献称为MW方法[4]。在实数解之后,主要的数据处理过程包括:非差到双差的映射关系确定,独立双差模糊度集的确定,双差宽巷、窄巷模糊度整数值的确定,双差无电离层相位模糊度约束值的确定,加入这些约束值后的平差计算。要详细进行阐释则需较长篇幅,本文对处理过程中用到的有关关系式进行简述,对于细节读者可参考有关文献[5-6]。
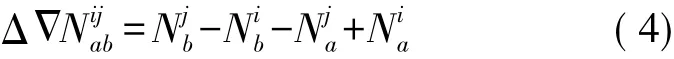
式中,下标a、b代表测站;上标i、j代表卫星;ΔΔ表示双差算子;式中右侧为有关站星非差模糊度,左侧为组合的双差模糊度,一个双差由4个非差构成。式( 4)为非差到双差的映射关系,通过该映射,可以将宽巷、窄巷、无电离层组合非差模糊度映射到相应的宽巷、窄巷、无电离层组合双差模糊度。对于一个双差,可形成一个映射向量,对于全部双差可得到一个映射矩阵。

式中,f1、f2代表GPS的两个载波频率值; Ni5jab为宽巷双差模糊度; N1ijab为窄巷双差模糊度; B3ijab为无电离层组合双差模糊度。式( 5)即反映了宽巷、窄巷、无电离层组合双差模糊度关系,在数据处理过程中,先通过原始观测值的MW组合计算非差宽巷模糊度,再利用映射关系得到宽巷双差模糊度值。初始无电离层组合双差模糊度由平差解算后的非差实数解映射得到,通过该关系式计算得到窄巷双差模糊度。

式中,b、σ为双差模糊度实数值及其方差; I为取整后的双差模糊度整数值; P0为概率值; n的上限实用上取一个小值[7]。式( 6)即为宽巷、窄巷模糊度实数值能否取为整数值的判定函数。由于计算精度有保证,因此可直接采用取整法来确定模糊度整数值,但需对取整是否合理进行判定。在一定置信水平α下,满足P0>1-α关系的认为是合理的,否则,双差模糊度仍按实数处理。在取得双差宽巷、窄巷整数模糊度值后,利用式( 5),计算无电离层组合双差模糊度新值,可得
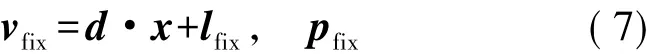
式中,d为式( 4)形成的非差到双差的映射向量; x为待定非差模糊度参数; lfix为初始无电离层组合双差模糊度与无电离层组合双差模糊度新值之差; pfix为权; vfix为验后残差。式( 7)构成对非差模糊度参数的约束关系。与相对定位不同,无电离层组合双差模糊度新值不能直接固定后重解其他参数,而只能是通过式( 4)的映射关系,对相应非差模糊度参数进行约束,采用附有约束条件的平差方法处理,解算全体参数。
四、计算与比较
1.数据情况
本文算例采用IGS网站提供的4个测站2013 年40天GPS观测数据,采样间隔为30 s,测站分布如图1所示。将BLYT设为待定站,其余为基站,待定站与最近的基站BILL距离为218.3 km,与最远的基站AZUl距离为299.8 km,设AZUl为主站。所有测站坐标通过IGS事后产品采用PPP计算,并作为已知值。广播星历和IGS快速星历由IGS网站下载,并将快速星历进行拼接,得到40天仅含快速预报轨道的精密星历文件。
2.计算方法
首先进行静态处理。对全天数据进行处理,分别采用1 h、2 h、3 h时段长度,每1 h滑动一个计算窗口,分别得到23、22、21个时段的计算结果,统计计算值与已知值差的RMS(均方差)。计算时分别采用IGS事后星历、快速星历和广播星历,并进行实数解和模糊度固定解计算。
之后进行动态解算。将BLYT设为动态站,利用快速星历和广播星历进行了0~3 h的动态定位,统计模糊度实数解结果。
3.计算结果
( 1)静态定位结果
BLYT测站静态定位结果与已知值差E、N、U分量RMS统计情况见表1。

图1 测站分布

表1 静态定位结果RMS值统计m
由计算结果可以看出,增加观测时长对提高定位精度有帮助;轨道精度对提高点位精度有明显影响;模糊度固定解在E分量相对实数解精度提高明显,N分量精度略有提高,U分量有的时段精度有下降情况; 3 h时段快速精密星历模糊度固定解,水平分量RMS达到毫米级精度,U分量精度达到1.5 cm; 3 h时段广播星历模糊度固定解,水平分量RMS达到1.2 cm,U分量精度达到2.9 cm。
采用事后精密星历结果与快速精密星历结果完全相同,说明快速预报的轨道精度已较高,与事后轨道计算结果一致。
( 2)动态定位结果
统计BLYT站分别利用广播星历和快速精密星历的动态定位结果,统计时均去除了前30 min数据,对余下的300个历元计算结果与已知值差E、N、U分量RMS、最大值、最小值进行统计,结果见表2。
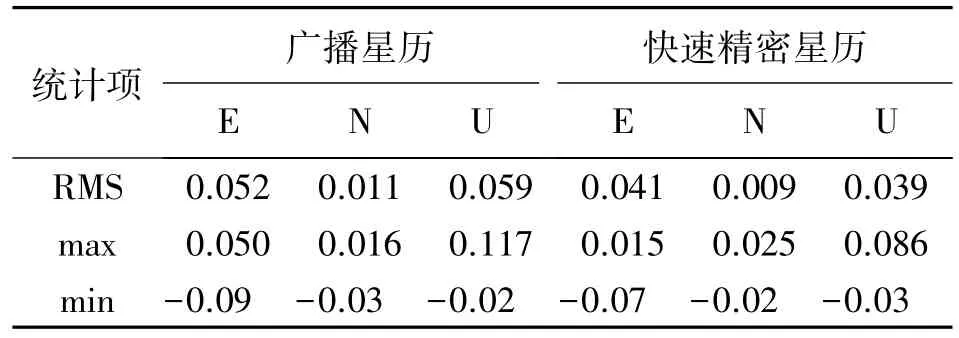
表2 动态定位结果统计 m
由计算结果可知,轨道精度对定位结果有明显影响;广播星历动态定位结果E分量RMS达到5.2 cm,N分量RMS达到1.1 cm,U分量RMS达到5.9 cm,均在厘米级。
五、结束语
本文对POP方法进行了扩展,在距基站中短距离的待定站静态、动态数据处理中,通过广播星历的应用,避免了对高精度轨道的依赖;在静态数据处理中,利用模糊度固定解,可以在水平分量精度上比模糊度实数解有所提高。实例表明了本文方法的可行性,具有一定的应用价值。
[1] SALAZAR D.Precise GPS-based Position,Velocity and Acceleration Determination: Algorithms and Tools[D].Spain: Technical University of Catalonia,2010.
[2] KOUBA J.A Guide to Using International GNSS Service ( IGS) Products[R].[S.l.]: NASA,2009.
[3] IGS.IGS_strategic_plan_2013_Final[EB/OL].[2014-07-20].http:∥www.igs.org/publications/IGS_ Strategic _Plan_2013_Final.pdf.
[4] 周巍,冯来平,王永收,等.QIF和MW模糊度分解方法的比较[J].大地测量与地球动力学,2013,33 ( 5) : 86-90.
[5] GE M,GENDT G,DICK G,et al.A New Data Processing Strategy for Huge GNSS Global Networks[J].Journal of Geodesy,2006,80( 4) : 199-203.
[6] GE M,GENDT G,DICK G,et al.Improving Carrierphase Ambiguity Resolution in Global GPS Network Solutions[J].Journal of Geodesy,2005,79( 1-3) : 103-110.
[7] ESOC.NAPEOS Mathematical Models and Algorithms [M].European Space Agency:[s.n.],2009.
The Improvement of Precise Orbit Positioning Method
REN Kai,TANG Yingzhe,FENG Laiping,OUYANG Mingda
通过对精密轨道定位( POP)方法的深入分析,从两个方面对其进行了扩展:一是利用广播星历进行数据解算,使得在距基站中短距离的待定站高精度定位时,避免了对高精度轨道的依赖;二是利用模糊度固定方法,将模糊度实数解扩展到模糊度固定解,解算精度得到了进一步提高。通过一组实际观测数据的处理,验证了本文方法的可行性,具有一定的实用价值。
GPS;精密轨道定位; PPP;模糊度固定
任 锴( 1973—),男,博士生,工程师,主要从事GNSS理论研究和数据处理。E-mail: Rpvt1204@ 163.com
P228.4
B
0494-0911( 2015) 11-0008-03
任锴,唐颖哲,冯来平,等.精密轨道定位方法的改进[J].测绘通报,2015( 11) : 8-10.
10.13474/j.cnki.11-2246.2015.0334
2014-11-16
国家自然科学基金( 41474015)
