PI自整定永磁伺服系统转动惯量的辨识研究*

马立新，徐镇乾，范洪成，黄阳龙

(上海理工大学光电信息与计算机工程学院，上海200093)

0 引 言

永磁同步电机在伺服系统的应用中，变化的电机转动惯量会对系统的性能造成较大的影响，特别是高精密数控机床、高性能机器人等对动、静态性能要求苛刻的场合［1］。如果转动惯量变大可能使系统不稳定，响应慢。如果转动惯量变小，虽系统响应变快，但会加大超调或震荡，甚至会造成低速时的转矩脉动［2］。

目前的研究大多是通过算法根据速度设定值与反馈值单纯对PI 参数进行优化，而忽略了它是一个多变量、内部强耦合的高阶非线性系统［3］，运行过程中很多参数会发生变化，PI 控制器的控制与电机参数密切相关，因此电机参数辨识才是电机PI 控制系统研究的关键［4］。

本研究针对永磁同步电机伺服系统中转动惯量变化问题，设计一种带PI 参数自整定的永磁同步电机转动惯量辨识系统并对其进行分析和研究。

1 永磁同步电机的矢量控制

1．1 坐标变换

利用坐标变换，可实现电机定子电流从静止坐标系到旋转坐标系之间的变换，简化了方程及空间矢量的计算求解，坐标变换如式(1)所示［7］。

Clarke 变换:即三相A、B、C 坐标系)到两相α、β坐标系之间的3/2 变换为:

Park 变换:即两相α、β 坐标系到两相d、q 坐标系之间的αβ/dq 变换为:

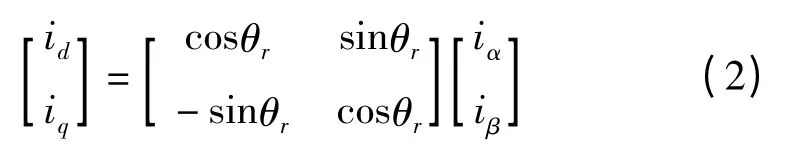
式中:θr—d 轴与A 轴之间的夹角［8］。

1．2 永磁同步电机数学模型

d、q 坐标系下永磁同步电机电压方程为:

式中:id，iq—直、交轴电流分量;ψd，ψq—直、交轴磁链;P—微分算子;ωr—转子角速度［9］。

d、q 坐标系下永磁同步电机电磁转矩方程为:

式中:Np—极对数，ψf—永磁体产生磁链［10］。

1．3 永磁同步电机PI 控制方法

永磁同步电机常采用的PI 控制方法关键就是要找到合适的Kp和Ki，由于伺服系统中参量的变化使PI 参数具有时变性，传统的PI 控制方法难以满足要求。采用基于PI 自整定的转动惯量辨识方法，对速度环PI 参数进行在线补偿［11］，其控制结构如图1 所示。

图1 转动惯量辨识值优化的PI 控制方式

2 转动惯量辨识方法的PI 自整定

转动惯量辨识方法有很多，如直接计算法、加减速法、MRAI 等。直接计算法通过复杂公式计算，要占用较多的计算机内存且精确度低。加减速法是一种离线式辨识方法，需要大范围加减速，使用场合要求苛刻。MRAI(模型参考自适应参数辨识)虽然是在线辨识方法，但是其程序的编写和调试非常困难［12］。

2．1 新型转动惯量辨识算法

在id=0 的控制方式下，由永磁同步电机d、q 坐标下的电磁转矩方程(4)得:

由式(5)可知电磁转矩T 和转矩电流iq成正比例关系，忽略系统摩擦，有机械运动方程得:

式中:ωr—转子转速，Tl—负载转矩，J—转动惯量，P—微分算子。

为防止启动或调速过中，电流过大而烧坏电机定子，一般速度PI 调节的输出会有一个限幅，即电流给定的最大值。当电机以最大电流作匀速运动时有:

令iq(max)=2in，则Te=2Tn。由式(6)得电机的加速度:

选取匀加速过程中的两个时间点t1、t2，在两个时刻分别记下电机转子转速ω1、ω2，有:

再令:iq(max)=in，则有:Te=Tn。本研究采用相同方法选取两个时间点t3、t4，使t4－t3=t2－t1，然后分别记录下此时电机转子的转速ω3、ω4，则有:

在两次加速过程中保持负载转矩Tl 不变，则有:

由式(11)得到了转动惯量的计算方法。

2．2 PI 参数自整定

伺服控制系统一般由外环速度环和内环电流环进行永磁同步电机的双闭环控制。电流环简化后，将其视作速度环中的一个环节，电流环为带有零点的二阶系统，传递函数如下:

式中:Tif—电流反馈通道滤波时间;Tsf=Tif+Ts;Ts—开关周期，都为时间常数;KP，τ—调整器参数;K =1/2Tsf。

速度环的截止频率一般比较低，忽略后的电流环传递函数可以近似降阶为:

式中:Km—简化后电流环单位比例增益。

式(13)为电流环调节器，速度环PI 控制的结构如图2 所示。

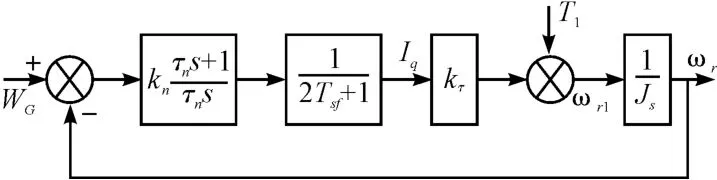
图2 速度环PI 控制结构图

本研究将速度环校正成典型Ⅱ型系统，速度环控制器采用PI 控制。伺服系统的开环传递函数为:

式中:kn，τn—调节器参数;Kt—转矩常数;J—电机转动惯量。

根据典型Ⅱ型系统设计参数公式:

式中:h—中频带宽，对于典型的二次型系统，h 值越小则系统的抗扰性就越好。

先来幻想一下：2030年的某天，你起床，在家中戴上一套VR装备，和大洋洲的客户开会。两小时后会议结束，你搭乘无人驾驶车辆，到隔壁城市和朋友午餐。午餐你点了一份用牛的干细胞培育出的人工牛排。晚间运动，你选择了以海岛为背景，慢跑在沙滩和夕阳的虚拟现实中。

当h ＜5 时系统的振荡次数将会增加。综合考虑系统的跟随性和抗扰性能的各项指标，根据经验取h =5。则有:

式中:h，Kt—常数，Kt可以由电机参数计算出;Tsf—时间常数，可以由电流环参数计算出。

根据式(11)计算出的转动惯量J，代入到式(17，18)中，得出PI 参数Kp和Ki补偿值，系统就会依据计算出的PI 参数对系统做出相应调整。

3 仿真实验结果研究

为了检验采用转动惯量辨识算法优化的PI 控制器性能，本研究以永磁同步电机为控制对象。电机初始参数如表1 所示。

表1 永磁同步电机参数

3．1 PI 参数自整定实现

本研究利用Matlab R2013b 平台进行试验，在Matlab 环境下建立的PI 参数优化仿真模型如图3所示。

图3 转动惯量辨识PI 补偿仿真框图

由图3 可见，在电机匀加速阶段，本研究分别采集4 个时间点t1、t2、t3、t4的速度值ω1、ω2、ω3、ω4。其中:t2－t1=t4－t3，框图中ω1为采集到的第一个速度值，ω2、ω3、ω4依次为延迟后采集到的速度值，然后将数值输入到转动惯量辨识模块，计算出的转动惯量值J 传输到速度环PI 自整定模块对PI 参数进行补偿。

3．2 仿真实验结果评估

本研究在Matlab 中搭建带有转动惯量辨识方法的永磁同步电机伺服控制系统模型，进行如下试验:启动时，初始负载转矩为0．2 N·m，转速为1 000 r/min;在0．15 s时，将负载加至2 N·m。本研究方法和传统方法速度波形如图4 所示。本研究方法和传统方法转矩波形如图5 所示。本研究方法逆变输出的A、B、C三相电流波形如图6 所示。

图4 转速波形曲线

由图中波形曲线可以看出，利用传统方法的系统速度和转矩超调较大，转速超调会使电机在启动阶段发生抖动，转矩的脉动会促使启动电流的增大，过大电流的冲击会对系统造成损害。而利用本研究方法的系统转速和转矩波形都要比传统方法波形曲线要平缓，而且从启动到速度稳定阶段速度无超调、响应快，实现永磁同步电机的平滑启动，说明该方法的系统稳定速度快，具有更好的动态性能;在速度稳定阶段实际速度非常接近设定值，提高了速度的精确度，速度误差率减少了0．16%左右，说明系统具有良好的静态性能。系统在负载变化时电机三相电流无尖峰，且为标准正弦波形，为坐标变换提供方便。采用本研究方法的系统具有良好的动、静态性能，不但可以提高系统响应速度，而且可以提高系统控制精度。

图5 转矩波形曲线

图6 本研究方法三相逆变输出电流波形曲线

4 结束语

笔者研究了带PI 参数自整定的永磁同步电机伺服系统转动惯量辨识问题，转动惯量在线辨识方法有利于提高永磁伺服控制系统的抗扰能力，使系统性能不受转动惯量变化的影响;提出了一种新型转动惯量辨识的PI 参数自整定优化算法，并与传统PI 控制方法在相同环境下进行仿真实验。

通过实验波形对比分析可知，相对传统方法来说该方法收敛快、无超调，且速度精确度相比传统方法高出0．16%左右;实现了转矩启动无尖峰，进而减小启动尖峰电流对控制系统的冲击，提高了系统可靠性，更具优越性。

下阶段，本研究会将该方法应用到高精密数控机床和高性能机器人等实际伺服系统中进一步完善，以提高系统的运行效率和控制精度，改善控制性能。

［1］LIU Hui-xian，LI Shi-hua． Speed control for PMSM servo system using predictive functional control and extended state observer［J］． Industrial Electronics，IEEE Transactions on，2012，59(2):1171-1183．

［2］陈伯时． 电力拖动自动控制系统运动控制系统［M］． 北京:机械工业出版社，2010．

［3］罗 慧，尹 泉，孙明明．交流伺服系统参数辨识方法综述［J］．伺服控制，2012，35(1):27-29．

［4］郭宇婕，黄立培，邱 阳．交流伺服系统的转动惯量辨识及调节器参数自整定［J］． 清华大学学报:自然科学版，2002，42(9)．1180-1183．

［5］周 虎． 永磁同步电机参数在线辨识算法研究［D］． 成都:电子科技大学自动化工程学院，2012．

［6］WU Yang-yang． Global Dynamic Sliding Mode Control of PMSM Speed Servo Systems Base on Extended State Observer［C］． Control Conference(CCC)，2013 32 and Chinese．2013:4432-44．

［7］徐 东，王田苗，魏洪兴．一种基于简化模型的永磁同步电机转动惯量辨识和误差补偿［J］．电工技术学报，2013，28(2):126-131．

［8］刘 竹．带PI 参数自整定的永磁同步电机伺服系统的设计与实现［D］． 长沙:湖南大学电气与信息工程学院，2013．

［9］丁文双．永磁同步电机PI 参数自整定［D］．南京:南京航空航天大学自动化学院，2012．

［10］韩亚荣，邱 鑫，朱德明．交流伺服系统转动惯量辨识方法［J］．电工电能新技术，2013，32(3):36-40．

［11］何 杰，王家军．基于SVPWM 的永磁同步电动机系统建模与仿真［J］．机电工程，2009，26(7):77-82．

［12］SENJYU T，KINJO K，URASSKI N，et al． Parameter measurement for PMSM using adaptive identification［J］．IEEE Trans． On Power Electronics，2011，45(12):1344-1354．