SSSC 与发电机励磁最优协调控制

樊 华，王 丹，毛承雄，陆继明，朱良合，张俊峰

（1.华中科技大学电气与电子工程学院，武汉430074；2.广东电网公司电力科学研究院，广州510080）

静止同步串联补偿器SSSC（static synchronous series compensator）作为柔性交流输电系统FACTS（flexible AC transmission systems）装置的重要一员[1]，具有提高系统稳定性、阻尼低频振荡、抑制次同步谐振和增加系统输送容量等方面的能力。与其他FACTS 装置相比，SSSC 具有控制范围广、响应快等特点[2-6]，能有效抑制互联系统区间低频振荡，提高输电线路的输送能力和电力系统的稳定性、可靠性[7]。

传统的可控串补TCSC（thyristor controlled series capacitor）装置采用晶闸管，暂态响应速度较慢。电抗器和电容器的并联或串联回路与电路电感有可能产生谐振[8]，其补偿出力还受线路电流影响。SSSC 克服了TCSC 的缺点，大幅改善了补偿性能。SSSC 向输电线路注入与线路电流正交、幅值可调且不受线路电流影响的容性或感性电压，注入电压产生的等效电抗不仅影响线路的输送功率，还能阻尼低频振荡[9]。文献[5]指出SSSC 中的串联变压器会产生很小的漏电抗，当SSSC 提供容性补偿时，漏电抗的压降会被自动补偿，因而在工频附近不会产生次同步振荡和谐振。即使线路有很高的补偿度，但是由于SSSC 对电抗有功部分的补偿，仍可以保持较高的X/R 比率，使得输电线路的有功输送能力维持在较高水平；文献[8]考虑SSSC输出电压相位与线路电流相位的垂直关系，计及直流母线电压的动态过程和逆变器的损耗，在d-q坐标系下建立SSSC 的恒阻抗模型，该模型通过双闭环比例-积分-微分PID（proportion integration differentiation）控制向线路中注入一个大小可控的阻抗，实现SSSC 快速潮流控制的功能。

本文结合传统的线性最优励磁控制LOEC（linear optimal excitation control），利用SSSC 恒阻抗模型，将SSSC 向输电线路注入的等效阻抗和同步发电机励磁电压作为控制变量，推导了带SSSC的修正Phillips-Heffron 模型，分析了新型LOEC 控制器的工作机理，并通过数值仿真对不同补偿量在各种工况下的特性进行了模拟。

1 带SSSC 的修正Phillips-Heffron 模型

线性最优控制理论突破了古典控制理论单输入、单输出控制的局限，实现了全状态反馈的最优励磁控制。LOEC 可以使远距离输电系统的静稳定极限大为提高，同时改善了系统遭受扰动时的阻尼特性。

常规的LOEC 只有励磁电压Efd一个控制量，其空间状态方程为

其中：X=[Δδ Δω ΔUt]T；U=ΔEfd；

在设计中采用的二次型性能指标为

由最优控制理论可得常规LOEC 的控制量，即

加入SSSC 后的单机无穷大系统模型如图1所示，其中SSSC 向线路注入的串联电压V˙ss可以等效为阻抗x。

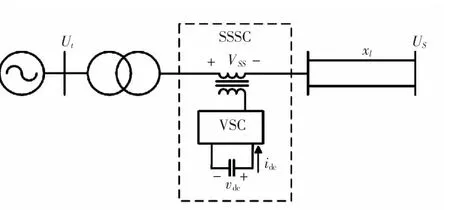
图1 带SSSC 的单机无穷大系统Fig.1 Single machine infinite bus with SSSC

线路中加入SSSC 后，同步发电机电磁功率为

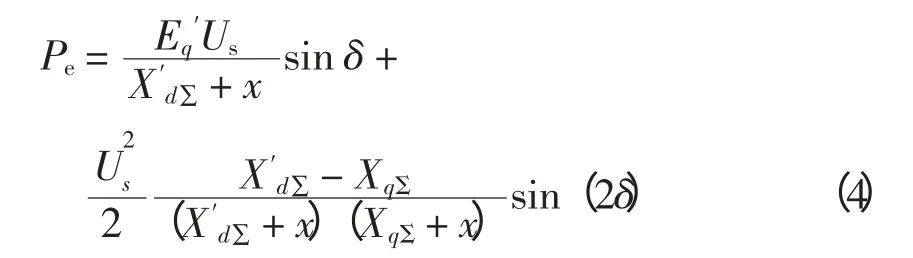
经偏差化后有

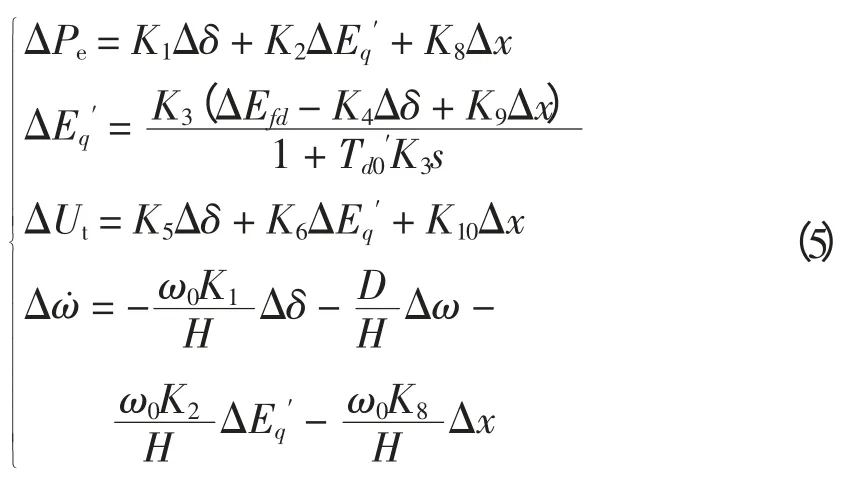
式中，K1～K6、K8～K10分别为与发电机运行状态和系统参数有关的系数，即

修正后的Phillips-Heffron 模型如图2 所示。由图2 可见，SSSC 向线路注入的阻抗通过两条通道为发电机提供电磁转矩，其中，一条通道与K8相关，直接作用于发电机机电振荡环节；另一条通道与K9、K10相关，经发电机励磁绕组后间接作用于发电机振荡环节。这两条通道可以为电力系统提供更多的阻尼，从而增强电力系统稳定性。

图2 带SSSC 的修正Phillips-Heffron 模型Fig.2 Modified Phillips-Heffron model with SSSC

系统状态空间方程为

可简写为

其中：X=[Δδ Δω ΔEq′]T；U=[Δx ΔEfd]T；

由于同步发电机q 轴暂态电势Eq′不易测量，同时，对于一套励磁装置，其首要任务是保持发电机机端电压的恒定，因此可用ΔUt替代ΔEq′。虽然功角δ 的测量并不困难，但在实际系统中选用ΔPe作为状态量会更方便。则状态变量[Δδ Δω ΔEq′]T与[ΔPeΔω ΔUt]T的关系可表示为

设状态变量Z=[ΔPeΔω ΔUt]T，则式（9）变为

设状态变量Z1=Z-T2U，则Z1=T1X，式（8）变为

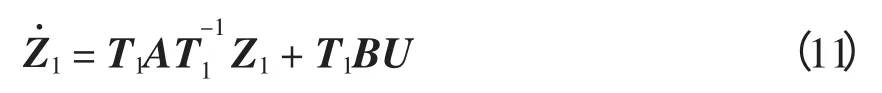
在设计中采用二次型性能指标，根据最优控制理论可得

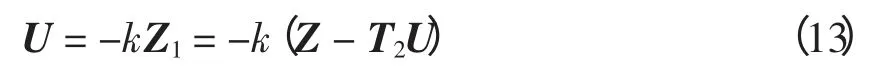
可得最优协调控制量为

在电力系统中，电压质量是首要指标[12]。为了满足正常运行中调整电压精度的要求以及提高微动态稳定功率极限的需要，应使机端电压偏差反馈的放大倍数较大，因此权矩阵Q 中与ΔUt对应的权重最大，机端电压受到的约束最强，动态品质最好；其次为使系统在动态过程中的振荡幅度及振荡次数减少，对角速度偏差Δω 应有足够的约束[13]。

2 仿真研究

基于单机无穷大系统对SSSC 与发电机励磁最优控制进行仿真研究。发电机采用三峡700 MW水轮发电机组[14]，仿真参数如下：xd=0.939，xd′=0.315，xq=0.69，Td0′=10.1；输电线路参数xT=0.13，xl=0.35；起始工作点P0=0.8，cos φ=0.875；权矩阵，为保证同步发电机电磁功率、机端电压和功角具有良好的动态品质和稳态性能，故选取R=diag（1，1），Q=diag（200，500，2 000）。

经计算可得系统矩阵为

SSSC 与发电机励磁最优协调控制的新型LOEC 控制器参数为

对于常规LOEC，权矩阵选取为R = 1，Q =diag（1，10，100），则相应的控制器参数为

在xmax不同的取值下，分别进行以下4 种扰动的数值仿真：①机端电压参考值上升5%；②原动机功率参考值上升5%；③一条线路断线并于3.5 s后重合；④升压变高压侧发生三相接地短路，0.1 s后故障切除。

2.1 xmax=0.06 时仿真分析

当xmax取值0.06 时，其仿真图形如图3～图6所示。由图3～图6 可见，装有新型LOEC 控制器的电力系统在受到小扰动后经过一次振荡就能恢复稳定，在受到大扰动时，振荡幅值有所减小，表现出比常规LOEC 控制器更好的性能。

图3 机端电压参考值上升5%的仿真波形Fig.3 Simulation curves of reference value of generator terminal voltage rises 5%

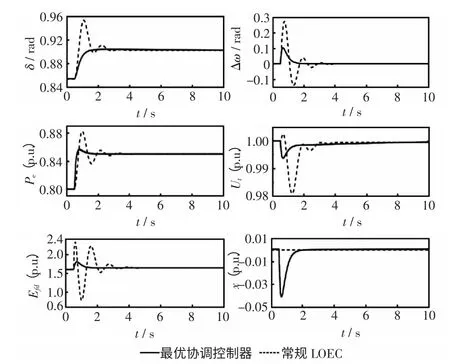
图4 原动机功率参考值上升5%的仿真波形Fig.4 Simulation curves of reference value of prime mover’s power riseing 5%

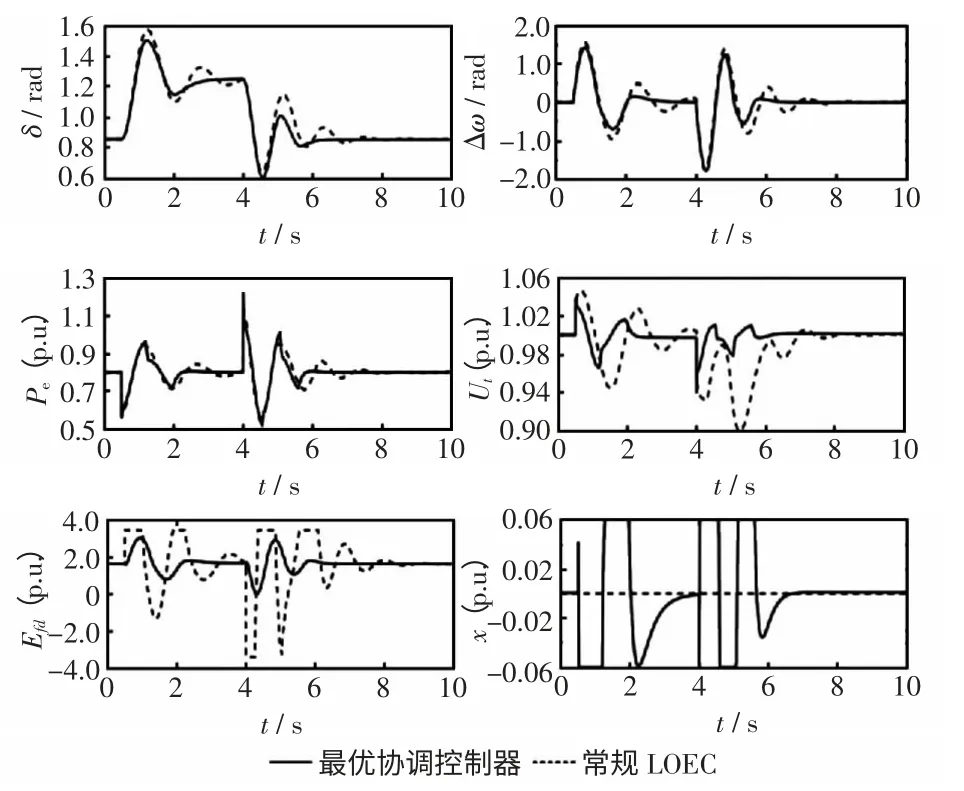
图5 一条线路0.5 s 断线3.5 s 后重合后的仿真波形Fig.5 Simulation curves of one line break at 0.5 s and recloses after 3.5 s

图6 升压变高压侧三相接地短路的仿真波形Fig.6 Simulation curves of three-phase grounding short circuit at high voltage side of booster transformer

2.2 xmax=0.1 时仿真分析

当xmax取值为0.1 时的仿真图形如图7～图10所示。由图7～图10 可见，当xmax增大时，电力系统在受到小扰动时的动态性能仍然良好，且受到大扰动时振荡次数明显减少，动态性能得到显著改善。

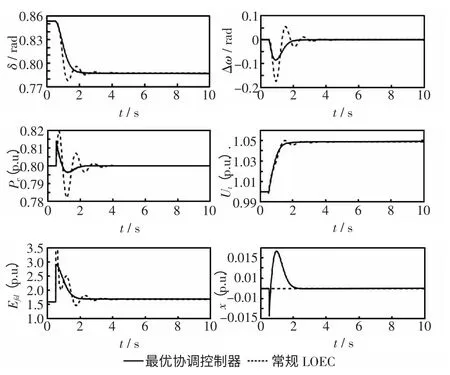
图7 机端电压参考值上升5%的仿真波形Fig.7 Simulation curves of reference value of generator terminal voltage rising 5%

图8 原动机功率参考值上升5%的仿真波形Fig.8 Simulation curves of reference value of prime mover’s power rising 5%

实际系统中，在动态性能显著改善、系统受小扰动时，补偿容量越小越经济。当xmax=0.06 时，系统在受到小扰动时具有良好的动态性能，并且受到大扰动时也能很快恢复稳定。故当补偿容量在0.06 时，能同时满足系统的动态性能需求和经济性要求。

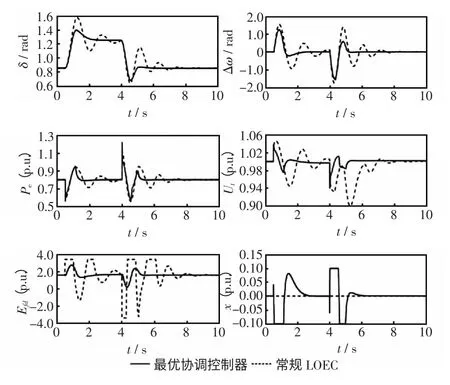
图9 一条线路0.5 s 断线、3.5 s 后重合的仿真波形Fig.9 Simulation curves of one line break at 0.5 s and reclose after 3.5 s

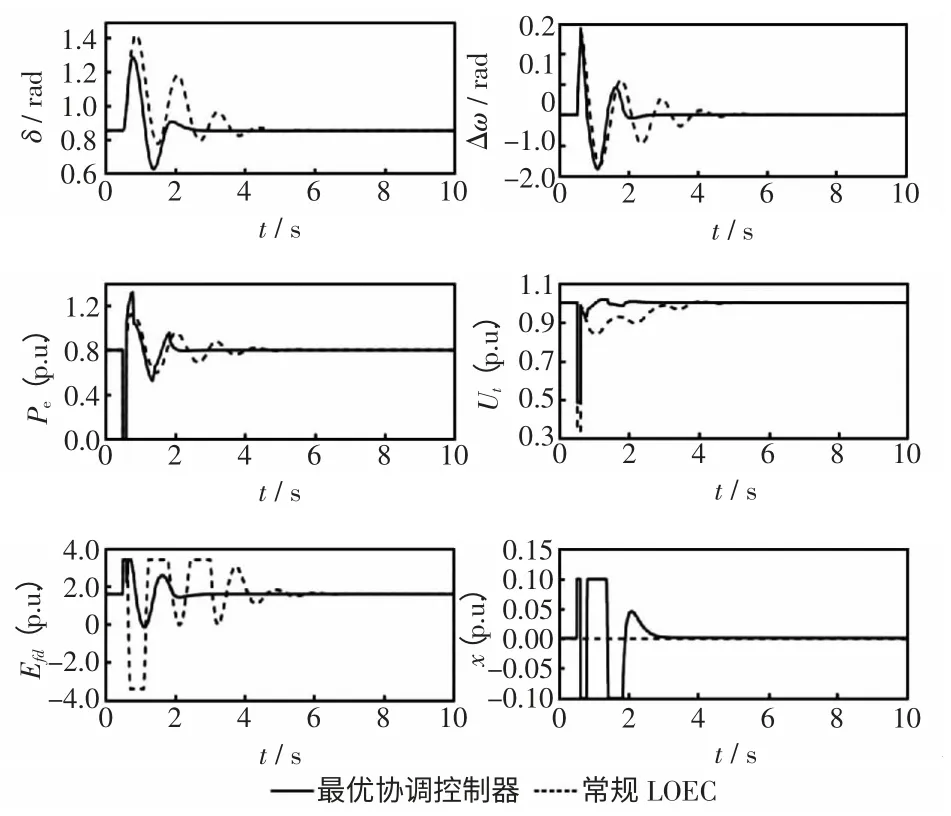
图10 升压变高压侧发生三相接地短路的仿真波形Fig.10 Simulation curves of three-phase grounding short circuit at high voltage side of booster transformer

3 结语

数值仿真结果表明，当SSSC 工作在阻抗补偿模式下时，可以将该补偿阻抗作为控制量，进行SSSC 与发电机励磁最优控制，能大大改善电力系统的稳定性。在电力系统发生小扰动后，很小的补偿阻抗就能有效抑制振荡，使得各状态变量仅经过一次小幅振荡就能恢复稳定；在电力系统发生三相接地短路、断线等大扰动后，若补偿阻抗限值过小，抑制振荡的效果不太明显，随着xmax不断增大，电力系统获得了更多阻尼，抑制振荡的能力明显提高。

[1]王树文，纪延超，马文川（Wang Shuwen，Ji Yanchao，Ma Wenchuan）. 灵活交流输电技术（Survey of flexible AC transmission system technology）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（3）：113-117，121.

[2]Poshtan M，Singh B N，Rastgoufard P. A nonlinear control method for SSSC to improve power system stability[C]//International Conference on Power Electronics，Drives and Energy Systems，New Delhi，India：2006.

[3]Juan Li，Sheng Dong，Xingfu Zhou. A nonlinear control approach to increase power oscillations damping by SSSC[C]//International Conference on Computer and Electrical Engineering，Phuket，Thailand：2008.

[4]Khuntia S R，Panda S. A comparative study of PSO-technique and fuzzy based SSSC controller for improvement of transient stability performance[C]//IEEE International Conference on Communication Control and Computing Technologies，Ramanathapuram，India：2010.

[5]Gyugyi L，Schauder C D，Sen K K. Static synchronous series compensator：a solid-state approach to the series compensation of transmission lines [J]. IEEE Trans on Power Delivery，1997，12（1）：406-417.

[6]Wang H F. Design of SSSC damping controller to improve power system oscillation stability[C]//IEEE 5th Africon Conference，Cape Town，South Africa：1999.

[7]吴政球，邹贤求，陈波，等（Wu Zhengqiu，Zou Xianqiu，Chen Bo，et al）.SSSC 在互联电力系统负荷频率控制中的应用（Application of SSSC in the load frequency control of interconnected power system）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：75-79，118.

[8]Othman H A，Angquist L.Analytical modeling of thyristorcontrolled series capacitors for SSR studies [J]. IEEE Transactions on Power Systems，1996，11（1）：119-127.

[9]赵洋，肖湘宁（Zhao Yang，Xiao Xiangning）. 利用SSSC阻尼电力系统低频振荡（Damping low frequency oscillation by static synchronous series compensator）[J]. 电力系统自动化（Automation of Electric Power Systems），2007，31（17）：40-44.

[10]张爱国， 张建华， 蒋程 （Zhang Aiguo，Zhang Jianhua，Jiang Cheng）. 静止同步串联补偿器的恒阻抗模型及其双闭环控制策略 （Constant-impedance model of static synchronous series compensator and its double closed loop control strategy）[J]. 电 网 技 术（Power System Technology），2010，34（3）：106-111.

[11]赵建军（Zhao Jianjun）. 静态同步串联补偿器机电暂态及电磁暂态特性研究（Study on Electromechanical and Electromagnetic Transient Performance of Static Synchronous Series Compensator）[D]. 北京： 中国电力科学研 究 院（Beijing：China Electric Power Research Institute），2005.

[12]王仲鸿，陈淮金. 电力系统最优分散协调控制[M]. 北京：清华大学出版社，1997.

[13]卢强，王仲鸿，韩英铎. 输电系统最优控制[M]. 北京：科学出版社，1982.

[14]陆继明，毛承雄，范澍. 同步发电机微机励磁控制[M].北京：中国电力出版社，2006.