Weibull分布最大值吸引场次序统计量的不等式及应用
2015-03-01钱荣华
钱荣华
(苏州市职业大学 数理部,江苏 苏州 215104)
Weibull分布最大值吸引场次序统计量的不等式及应用
钱荣华
(苏州市职业大学 数理部,江苏 苏州 215104)
主要讨论Weibull分布极值吸引场下的随机样本及非随机样本的次序统计量的一个不等式,并给出两个简单的应用.
最大值吸引场;Weibull分布;次序统计量
假设{X,Xn│n≥1}为非退化独立同分布(i.i.d.)随机变量序列,具有共同的分布函数F.记部分和为自Hsu与Robbins (1947)[1]引入完全收敛的概念后,出现了很多结果. 最初考虑级数
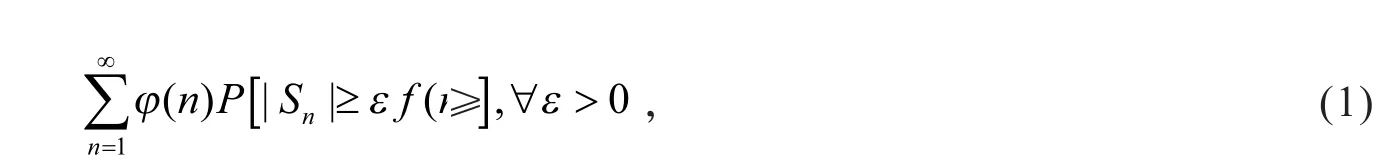
收敛的条件.很多文献都研究了这个问题.如,Hsu与Robbins[1](1947)、Erd s (1949[2],1950[3])考虑了当φ(x)=1,f(x)=x时的结果;当0<p<2时,Baum、Katz[4](1965)对进行了讨论,Bingham、Goldie[5](1988)对更一般的情况进行了研究.
众所周知,次序统计量在实际问题中有着广泛的应用,对其性质的讨论历来是一个热点问题,严继高等[6]考虑了i.i.d.的随机变量,在其分布函数属于极值分布为Fre'chet分布的最大值吸引场情况下相应次序统计量的精致渐近性,且考虑了样本容量是一个计数过程的结果,本文旨在考虑极值分布是Weibull分布的最大值吸引场的情况下的一个不等式,并给出两个简单的应用.
1 基本概念介绍
定义1 设X,X1,X2,…为非退化i.i.d.的随机变量序列,其共同的分布函数为F(x),x∈R.若存在适当的常数cn>0,dn∈R及分布函数H(x)使得

则称随机变量X(或分布函数F)属于极值分布H(x)的最大值吸引场,记作X∈MDA(x)或F∈MDA(H)
由著名的Fisher-Tippett定理知,极值分布H(x)只有三种类型:Fre'chet分布,Gumbel分布,Weibull分布Ψα(x),其中α>0为参数.
假设{Y,Y,i≥1}为i.i.d.的随机变量序列,且与随机变量序列{X,Xi│i≥1}相互独立,P(Y>0)=1,为常数.记则N(t)为一更新计数过程.定义随机样本X1,的次序统计量为,相应的非随机样本X1,X2,…,Xn的次序统计量为
2 引理和主要结论
先给出几个重要的引理.
引理1 The df F belongs to the maximum domain of attraction of,α>0,if and only ifandfor some slowing varying function L.

where the norming constants cncan be chosen as
引理2 (1) Ifl is slowly varying then for any chosen constants A>1,δ>0 there exists X=X(A,δ) such that
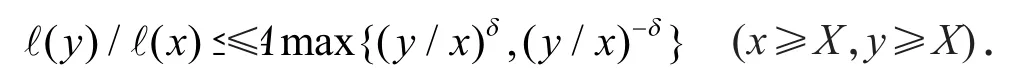
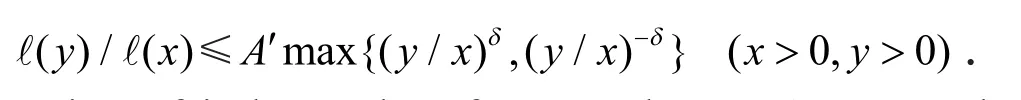
(3) If f is regularly varying of index ρ then for any chosen A>1,δ>0 there exists X=X(A,δ) such that
再给出本文的主要结果.
定理1 设F∈MDA(Ψα),θ,s均为任意正常数,则对任意ε>0,当n充分大时有
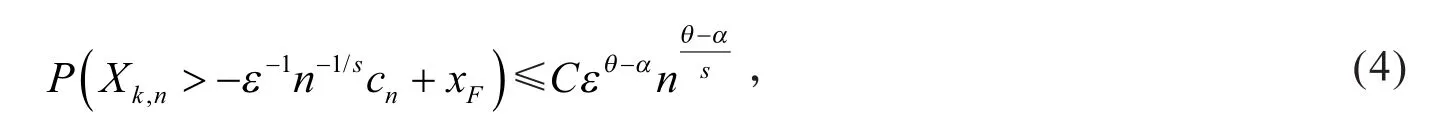
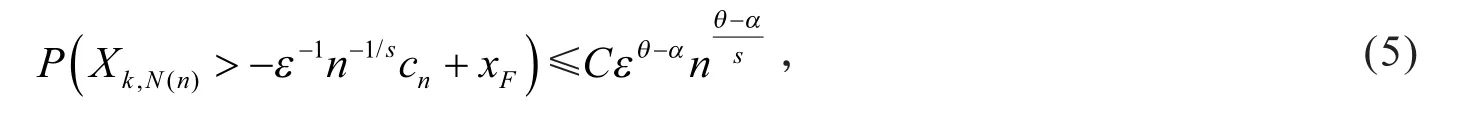
其中C为与ε无关的正常数.
类似于经典的Baum-Katz定理,给出如下两个简单的应用.
命题1 设,则对任意0<s≤p≤r≤α有

特别地
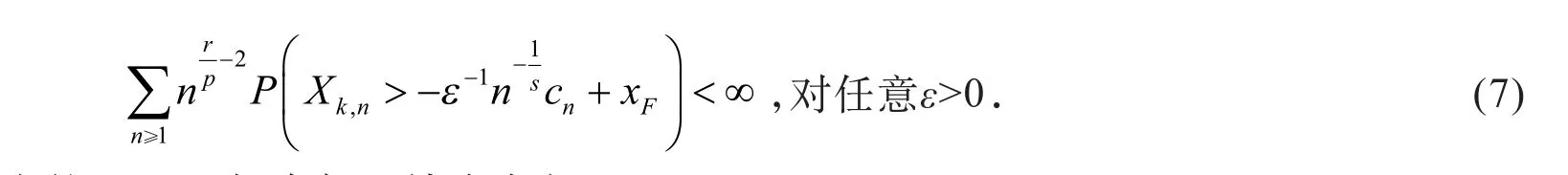
特别地,当命题1中的s=r=ρ时,有如下结论成立.
命题2设F∈MDA(Ψα),则对任意0<p<α有

特别地

3 结论的证明
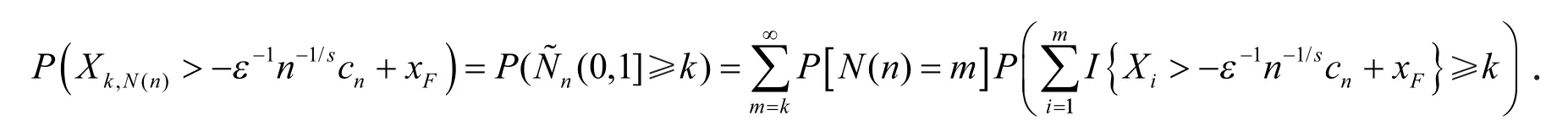
由于{Xi,i≥1}为i.i.d.的随机变量序列,故由Markov不等式及Cr-不等式得
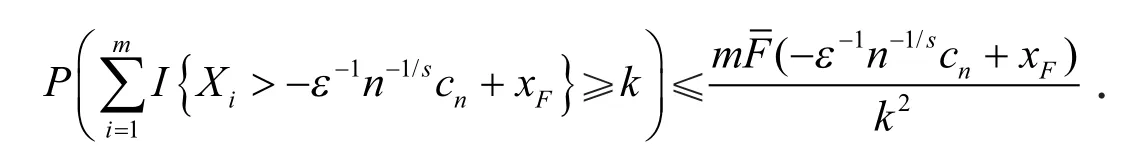
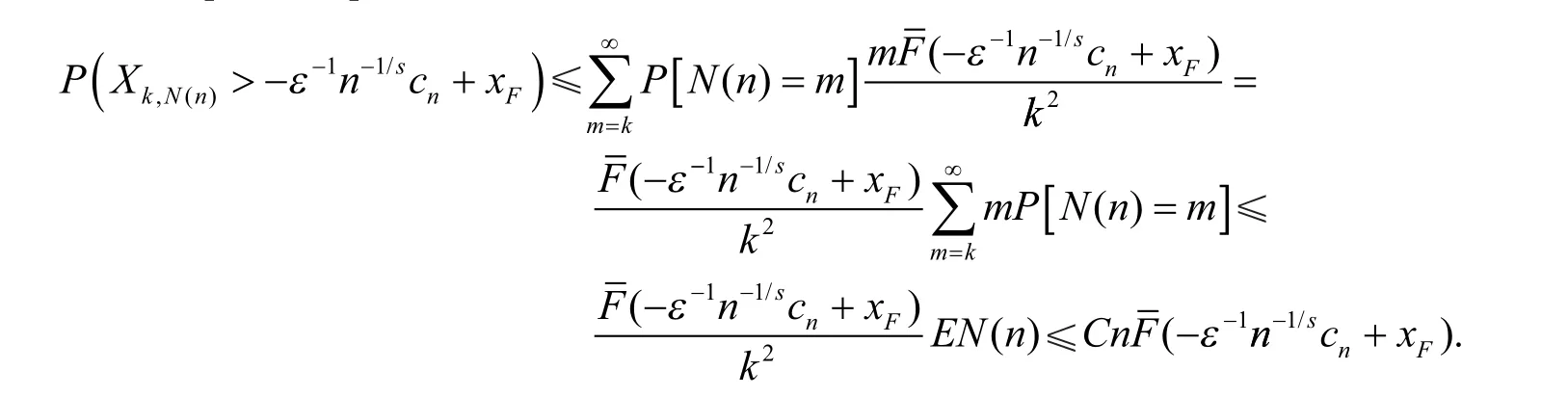
类似可得
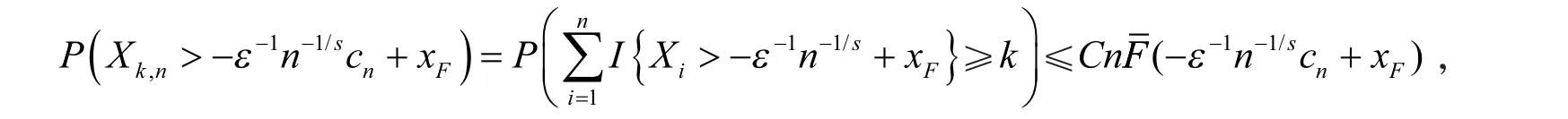
故要证结论成立,只需
事实上,由于F ∈ MDA(Ψα),故存在某正值缓变函数L(x)使得,又,从而. 故对充分大的n,不妨设则
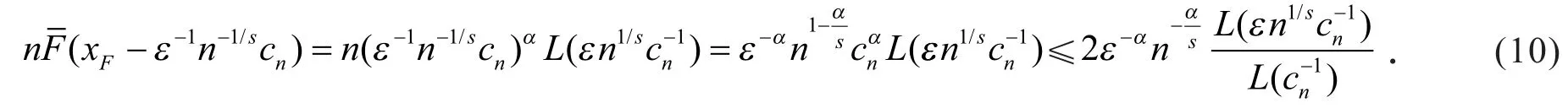
由Potter定理[7]知,对充分大的n,存在A=A(θ)>1使得故由式(10)得
An Inequality for Order Statistics in Maximum Domain of Attraction of Weibull Distribution and its Applications
QIAN Rong-hua
(Department of Mathematics and Physics,Suzhou Vocational University,Suzhou 215104,China)
The paper mainly discusses an inequality for order statistics of a random sample and a non-random sample that belong to the maximum domain of attraction of Weibull distribution,and some applications are also presented.
maximum domain of attraction;Weibull distribution;order statistics
O212
A
1008-5475(2015)01-0041-03
2014-10-23;
2014-11-21
钱荣华(1978-),女,江苏常熟人,主要从事概率统计研究.
