基于MATLAB的数学实验教学研究

文/卢月莉

基于MATLAB的数学实验教学研究

文/卢月莉

本文通过实例演示MATLAB软件在大学数学实验教学中发挥的作用，说明学生可以通过掌握MATLAB来提高对数学知识的理解和解决实际问题的能力。

MATLAB；教学；数学实验

1.引言

随着计算机的普及和发展，从20世纪90年代中期开始，数学实验作为高等数学教学改革的产物在国内高等院校诞生，它以与传统数学教学不同的方式在高等数学教育中引起了广泛的兴趣。数学实验旨在引导学生借助数学软件理解抽象的数学理论、自主探究和研究数学问题以及数学的应用问题的实践过程[2]。数学实验课程的开设和普及对于推动数学课程教学的全面改革，加强素质教育具有十分重要的现实意义[3]。

在多种支持数学实验的软件中，最具有代表性的是MATLAB、Mathematica和Maple，它们各有特色。MATLAB程序设计语言集成度高，语句简洁高效，具有出色的数值运算和绘图功能，利用各种各样领域专业专家编写的工具箱，可以高效、可靠地解决各种各样的问题，具有不可替代的优势。本文通过实例演示MATLAB软件在微积分问题的求解、非线性方程的求解和三维空间图形的绘制等方面的应用，以期培养学生运用计算机研究和学习数学的能力，进而提高学生的创新能力。

2.微积分问题的MATLAB求解

利用MATLAB软件的符号运算工具箱，可以很容易地求解极限、微分、积分等微积分基本问题。需求特别注意的是，在求解之前应该先声明自变量为符号变量，否则会出现错误提示。

2.1 极限问题的求解

极限问题在MATLAB软件中可以使用limit()函数直接求出，其调用格式为limit(f,x,x0)，表示求函数f当x→x0时的极限，若x0为∞则用inf表示。

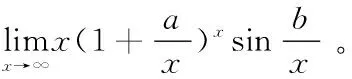
解 首先声明a、b和x为符号变量，然后定义函数表达式，最后调用limit()可以直接求出极限。编程如下：

>>symsxab；f=x*(1+a/x)^x*sin(b/x);limit(f,x,inf)

运行结果为：b*exp(a)

2.2导数问题的求解

如果函数和自变量都已知，且均为符号变量，则可以用diff()函数解出给定函数的各阶导数，其调用格式为diff(f,x,n)，f为给定函数，x为自变量，n为导数的阶次。

functiondn=hdiff(y,x,t,n)

ifn==1,dn=diff(y,t)/diff(x,t);

else

dn=diff(hdiff(y,x,t,n-1),t)/diff(x,t);

end

end

再在命令窗口输入：

>>symst;x=exp(2*t)*cos(t)^2;y=exp(2*t)*sin(t)^2;

>>d3=simplify(hdiff(y,x,t,3))

运行得结果：>>d3=-(- 8*cos(t)^4 + 16*sin(t)*cos(t)^3 + 8*cos(t)^2 - 12*sin(t)*cos(t) + 3)/(exp(4*t)*(16*cos(t)^10 - 16*sin(t)*cos(t)^9 + 32*sin(t)*cos(t)^7 - 20*cos(t)^6 + 4*sin(t)*cos(t)^5))

2.3 积分问题的求解

运用MATLAB中的int()函数可以求解定积分或无穷积分问题，调用格式为int(f,x,a,b)，其中x为自变量，(a,b)为积分区间，无穷以inf代替。

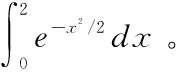
解MATLAB命令窗口输入：

>>symsx;y1=int(exp(-x^2/2),x,0,2)

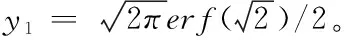
3.一般非线性方程的求解

对于一般的非线性方程，MATLAB提供了fsovle()函数来求解它的一个实数根，其调用格式为x=fsolve(fun,x0)。其中，fun为所求方程的M-函数或匿名函数描述，x0为初始搜索点，程序将从该点以逐步减小误差的算法搜索出满足方程的实根x。

例3 求方程e-(x+1)2+π/2sin(5x+2)=0 的根。

解 首先用ezplot()函数绘制出如图1所示的曲线，该曲线与横轴的所有交点均是方程的解。

>>ezplot('exp(-(x+1)^2+pi/2)*sin(5*x+2)')

>>line([-4,2],[0,0])

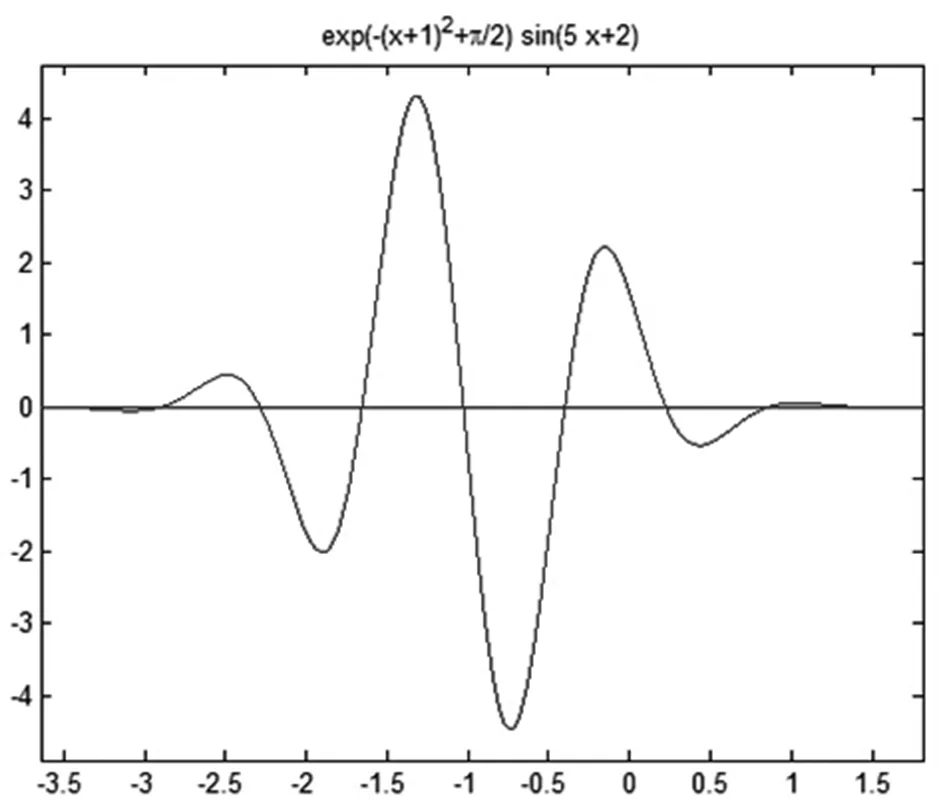
图1 例3中的方程曲线

从得出的曲线可以看出，该方程有多个实根。我们接着任选一点作为初值，利用fsolve()函数求出方程更精确的解，如x0=-1附近的解编程为：

>>fun=@(x)exp(-(x+1)^2+pi/2)*sin(5*x+2);

>>x=fsolve(fun,-1)

结果为x= -1.028318530717959，代入原方程，得f= -5.886413288211306e-016，可见得到的解精度比较高。

4.三维空间图形的绘制

在高等数学中，由于很多学生缺乏空间想象能力，空间解析几何是学生最不容易理解的知识之一。而MATLAB提供了一系列直观、简单的三维图形绘制命令与函数，可以将实验结果用可视的形式显示出来，有助于学生建立空间想象能力和理解函数。

例4 绘制函数z=sinxy的表面图，并剪下x2+y2≤0.52的部分。

解 在图形绘制语句中，若函数值为NaN，则相应的部分不绘制出来，因此可以在MATLAB命令窗口输入：

>> [x,y]=meshgrid(-pi:0.1:pi);

>>z=sin(x.*y);ii=find(x.^2+y.^2<=0.5^2);

>>z(ii)=nan;surf(x,y,z)

运行结果如图2所示。在默认视图中，可以观察到被剪下部分并没有显示出来。但是MATLAB提供了修改视角的功能，用户可以通过图形窗口工具栏的旋转按钮或者view()函数对图形进行旋转，从任意角度观察三维图形。图3为view(-40,60)的运行结果。

图2 z=sinxy的默认视图

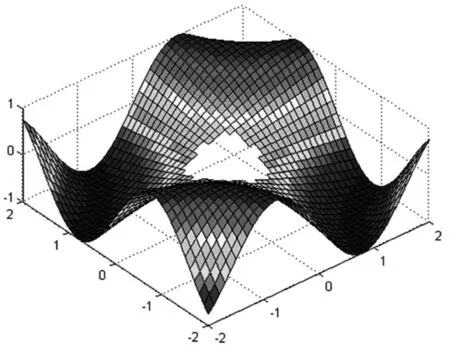
图3 z=sinxy的俯视图(view(-40,60))

5.结语

本文通过几个实例演示说明，将MTALAB软件引入大学数学实验教学中，有利于培养学生学习数学的兴趣和应用数学的能力，目的是让学生在掌握了数学问题的MTALAB求解方法以后，即使对某些数学公式理解得不太透彻，也能轻易地利用计算机求解复杂的数学问题，逐步解决大学里长期存在的“一方面数学很有用，另一方面学生学了数学以后却不会用”[2]的矛盾现象。

[1]薛定宇，陈阳泉.高等应用数学问题的MATLAB求解(第三版)[M].北京：清华大学出版社，2013.

[2] 韩明，王家宝，李林. 数学实验(MATLAB版)[M].上海:同济大学出版社，2012.

[3] 罗汉，万中，王利平.数学实验课程的内容体系及教学模式[J].数学理论与应用，2001，21(4):105.

卢月莉(1988—)，女，壮族，广西南宁人，硕士，河池学院助教，研究方向：应用统计。

TP

A

2095-9214(2015)02-0115-02

河池学院数学与统计学院)

广西高校科学研究项目KY2015ZD103