高超声速壁板流固热耦合建模与分析



高超声速壁板流固热耦合建模与分析

杨武，韩景龙

(南京航空航天大学 航空宇航学院，江苏 南京210016)

摘要：基于气动热、气动弹性双向耦合的热气弹分析方法，建立了高超声速三维壁板流固热耦合分析模型。气动力计算采用三阶活塞理论，气动热计算采用参考温度法，热传导和结构响应采用有限元方法进行。研究了不同边界条件、飞行轨迹下耦合方式对三维壁板热气弹响应的影响。结果表明：不同流固热耦合机制对高超声速气流中壁板响应预测影响各不相同，表明了研究的必要性。

关键词：高超声速；热气动弹性；三阶活塞；双向耦合；参考温度法

壁板非线性热颤振分析是现代高速飞行器研发所面临的重要技术问题。非线性壁板颤振分析中，一般采用冯卡门(Von - Karman)非线性应变-位移关系[1-2]。常用非定常气动力理论主要有三个:高阶活塞理论、基于Euler方程的方法以及基于Navier-Stokes方程的方法。在超声速以及高超声速条件下，活塞理论均能为壁板颤振分析提供合理的气动力理论[3-4]，是一种较为成熟、应用较为广泛的气动力理论。气动热计算方法有3种：1)数值模拟方法；2)工程近似方法；3)边界层外的无粘数值求解和边界层内的工程方法相结合来计算高超声速飞行器表面热流。

大量文献已对壁板热颤振进行了研究。然而，由于热气弹问题的复杂性，大多数文献均忽略结构变形对温度的影响。文献[5]的研究表明，结构变形对壁板前缘气动加热产生的影响应在设计中给予考虑；文献[6]第一次提出了用于壁板颤振研究的气动热-气动弹性双向耦合的分析方法，并对二维壁板进行研究。文献[7]基于双向耦合方法对二维曲板进行了相应的研究。本文基于气动热、气动弹性双向耦合的颤振分析方法，对于三维碳-碳复合材料层合板进行了流固热耦合分析。其中气动力计算采用三阶活塞理论，气动热采用参考温度法，热传导和结构响应采用有限元方法进行。

1双向耦合的分析思路

传统的壁板热气弹分析，仅根据初始的压力分布计算气动热(忽略了弹性力-惯性力-气动力3者耦合后的气动力改变对气动热的反馈影响[8])，进而计算温度分布或直接采用恒定的温度场。双向耦合[6](见图1)采用热模块与气弹模块的松耦合，既考虑温度场对弹性变形的影响(路径①)，也考虑了弹性变形对气动加热的影响(路径②)，对热气弹这一多学科问题加以求解。

首先计算非定常气动力形成的飞行器表面热流分布，再进行结构热传导分析，得到相应的温度场，最后进行热环境下的气动弹性计算。

图1　基于双向耦合的热气动弹性模型Fig.1　Fluid-Thermal-Structural Coupling model

2理论基础

2.1　壁板前缘气流参数计算

采用如图2所示的飞行器表面壁板。在计算气动力前，首先要得到壁板前缘即位置3处的气流参数。假设尖楔其余部分均为刚体。

图2　典型高超声速飞行器结构Fig.2　Representative hypersonic flight vehicle configuration

采用斜激波关系式计算3处的气流参数,θ为尖楔与水平面的夹角，β为激波角，γ为空气的比热比(可取1.4)，M1，p1，T1，ρ1为远前方气流参数，M3，p3，T3，ρ3为壁板前缘气流参数。

(1)

(2)

(3)

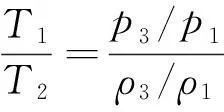
(4)

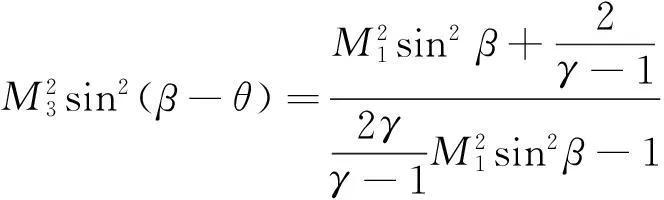
(5)

2.2　求解高超声速无粘气动力

采用非线性三阶活塞理论计算气动力p4。

(6)

其中，w为z方向位移，γ为比热比。

通过等熵关系求得壁板的当地压力分布和其余当地气流参数T4，M4，U4，提供给下一步的气动热计算。由活塞理论以及当地弹性变形，气动热的计算包含气动弹性的影响，实现气动热和气弹系统的双向耦合。

2.3　气动热计算

气动热计算采用工程上广泛使用的Eckert参考温度法，公式如下：

T*=Te+0.50(Tw-Te)+0.22(Tαw-Te)

(7)

其中为Te当地气流温度，Tw为壁面温度，Taw为恢复温度，Taw计算公式如下：

(8)

Pr为普朗特数，这里取0.86。

使用萨特兰公式和状态方程式计算参考密度和参考粘性系数[5]。通过式(9)求得参考雷诺数，然后通过雷诺比拟式得到斯坦顿数，最后通过热流公式(12)计算表面热流。

(9)

(10)

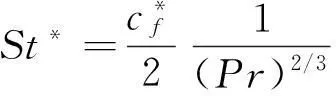
(11)

(12)

另外，考虑热辐射散热，假设壁板的表面为非黑体，辐射发射率为0.7，则辐射散射公式为

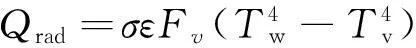
(13)

σ为斯坦福常数，其值为5.669×10-8。

2.4　热传导与气动弹性计算

热传导与气动弹性计算采用有限元方法进行。

3分析模型及计算流程

典型高超声速碳-碳复合材料壁板结构尺寸如图3示。

图3　典型高超声速碳-碳层合板Fig.3　Representative carbon-carbon hypersonic skin panel

壁板和加强板均采用碳-碳复合材料层合板，内部0/90铺层角度，外部为45°铺层角。壁板采用5层铺层方式，加强板采用4层铺层方式。热模型对壁板采用体单元，对加强板采用板单元，而结构模型对两者均采用板单元。

考虑两种x方向平移的结构边界条件：(1)自由膨胀，(2)线弹簧。两种情况下，壁板前缘和后缘在旋转自由度和z方向是完全约束的，y方向允许其自由膨胀(壁板中心施加y方向约束防止刚体运动)。第1种情况在x方向是自由膨胀(壁板中心施加x方向约束防止刚体运动)。第2种情况中，前缘在x方向约束，线弹簧被施加在壁板后缘，弹簧常数的变化使用E11*h的百分比。

准静态求解过程如图4所示。

图4　准静态流固热耦合求解过程原理图Fig.4　Fluid-thermal-structural solution procedure

流固热耦合参数交换如图5所示。S-1234代表着完整的交互作用，而S-1030仅包括箭头①、③。

图5　流固热耦合类型Fig.5　Types of fluid-thermal-structural coupling

考虑两种飞行轨迹：(1)常马赫数飞行(Ma12)；(2)恒定速率上升(300 s内Ma由2升到12)。

4结果分析

计算中的结构和气动参数如下：a=0.304 8 m，b=0.254 m，kx=30.3 W/(m·K)，ky=30.3 W/(m·K)，c=711.79 J/kg/K，E11=E22=10.34×1010Pa，α11=α22=1.044×10-61/K，v=0.3，Tinitial=294.44 K，G12=1.723 5×1010Pa，θ=5°，x3=1.524 m，q∞=9.575×104 Pa。每种飞行轨迹中，板初始无应力且均为294.44 K。

4.1　常马赫数飞行轨迹

对自由膨胀(0%spring)和适当面内膨胀抵抗(10%spring)进行分析，采用壁板中心位移、壁板气流方向中心线变形、温度以及失效因子来定量的表征4种耦合方式导致的响应的区别,如图6～图7所示。

a 中心位移：0% spring

b 壁板变形：0% spring

c 壁板温度：0%spring

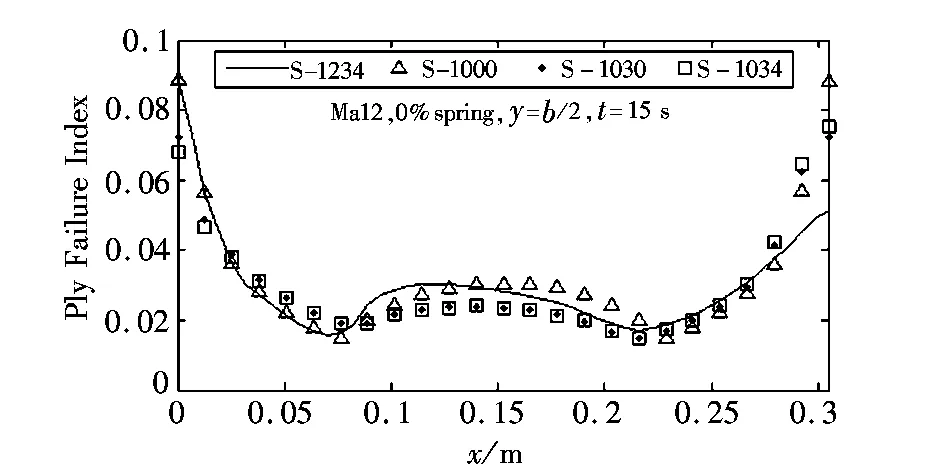
d 失效因子：0% spring图6　Ma12，0% spring下准静态响应结果Fig.6　Quasi-static response results: Mach 12,0% spring

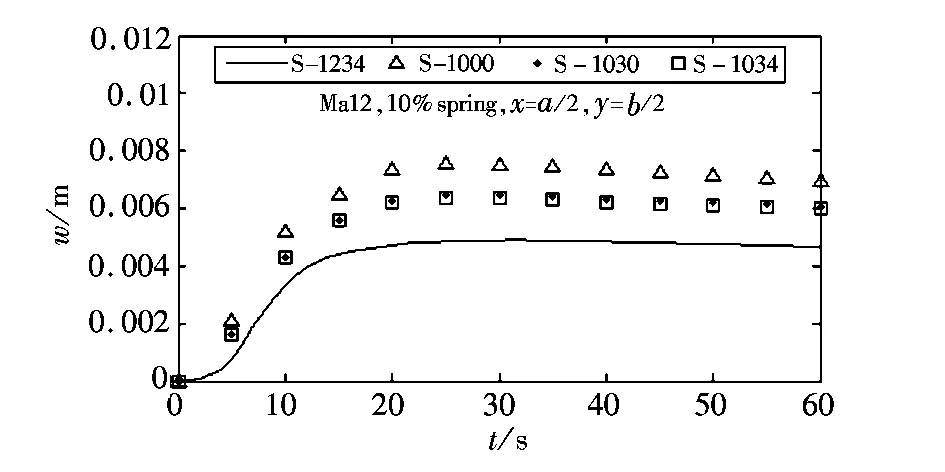
a 中心位移：10% spring

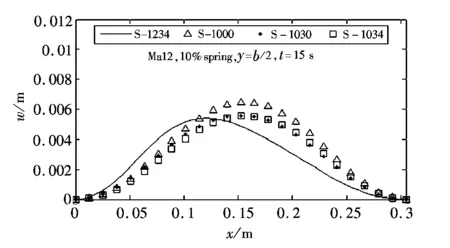
b 壁板变形：10% spring

c 壁板温度：10%spring

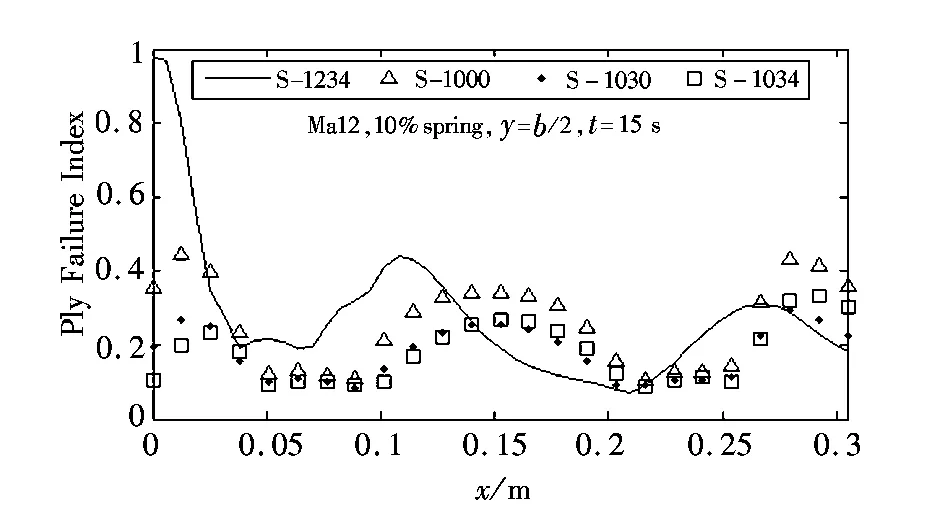
d 失效因子：10% spring图7　Ma 12，10% spring下准静态响应结果Fig.7　Quasi-static response results: Mach 12,10% spring

由图6、图7可以看出，10%spring下的最大位移近似为0% spring的10倍，这是由于10% spring下产生的面内热应力导致壁板屈曲。0% spring下，S-1030、S-1034、S-1234壁板变形很接近，而S-1000过度预测壁板变形接近33%，这是由于S-1000下更高的温度导致z方向更大的温度梯度，导致更大的热弯曲载荷。对10% spring来说，与S-1030和S-1034相比，S-1234导致不对称的壁板变形(最大位移发生在大约40%弦长位置)，而S-1030与S-1034的变形很接近，这表明结构变形对表面压力的作用(图5中箭头4)对变形影响很小，即变形主要是由热载荷引起的；S-1000过度预测了壁板变形近似10%，这表明，壁板变形(10% spring)依赖于瞬态壁温和结构变形对气动生热和因而产生的热载荷影响。

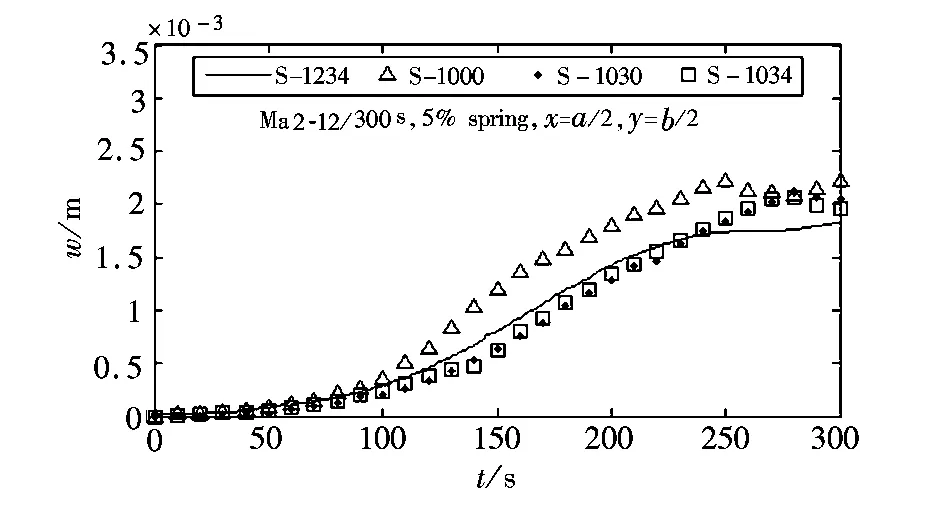
a 中心位移：5% spring

b 壁板变形：5% spring

c 壁板温度：5% spring

d 失效因子：5% spring图8　Ma 2-12，5% spring下准静态响应结果Fig.8　Quasi-static response results：Mach 2-12,5% spring

S-1000得到的温度，与S-1030、S-1034相比，在两种情况下分别高了6%和16%；S-1030和S-1034的温度是完全一致的，这是由于气动热耦合分析的类型是一致的；S-1234由于变形的影响预测了不均匀的壁板温度(但是均值近似于S-1030和S-1034)。近似为0.5壁板厚度变形的最大位移导致最大壁温升高大约1.5%，而10% spring条件下(最大位移大约3到4倍厚度)最大壁温上升到大约15%。

四种耦合方式的失效因子在0%spring条件下基本一致，且均在0.1以下，应力水平很低;而10% spring条件下，失效因子则大得多。10%spring下，S-1234的失效因子比另外三种耦合方式大很多，连同10%spring情况下的变形和温度，表明气动热和结构变形相互耦合的重要性，即结构变形改变气动生热，随之产生的温度分布又影响结构变形。

4.2　恒定速率上升

对适当面内膨胀抵抗(5%spring，20%spring)进行分析，采用壁板中心位移、壁板气流方向中心线变形、温度以及失效因子来定量的表征四种耦合方式导致的响应的区别，如图8、9所示。

5%spring条件下，中心位移在整个条件下一直增加，这是由于导致壁板屈曲的面内热应力随着温度上升持续增加。

a 中心位移：20% spring

b 壁板变形：20% spring

c 壁板温度：20% spring

d 失效因子：20% spring图9　Ma 2-12，20% spring下准静态响应结果Fig.9　Quasi-static response results： Mach 2-12,20% spring

300 s时壁板变形大约在1倍壁板厚度，微小的区别还是很明显的。S-1234预测了不对称的变形，位移峰值大约在0.45弦长处。比较S-1030与S-1034，可以看出结构变形对表面压力的影响是很明显的，壁板前半部分压力(S-1034)增加降低对应的位移，后半部分压力减小导致位移变大。

壁板温度方面，S-1234预测了不均匀的温度分布。最高壁面温度上，S-1000和S-1234分别比S-1030和S-1034高6%和4%。

20%spring情况下，每种耦合方式在不同时间(均大于120 s)呈现突变跳跃现象，这种结果，连同5%spring情况，表明面内边界条件的刚度增加会降低遇到突变跳跃前的飞行时间。S-1034和S-1234大约在130 s时发生突变跳跃，而S-1000和S-1030大约在190 s时发生突变跳跃，前两种考虑了壁面压力的影响，后两种没有。总的来说，结果表明壁面压力会影响突变跳跃发生的时间，瞬态热载荷可单独诱导突变跳跃的产生。

5结论

基于气动热-气动弹性双向耦合的热气弹思路，对高超声速三维壁板进行热气动弹性响应数值仿真，得到如下结论：

(1)准静态响应下，流固热耦合的重要性是面内结构边界条件的强函数。自由膨胀边界条件移除了耦合的重要性。然而，相对温和的防面内膨胀会导致10倍数量级的最大结构变形。

(2)抑制面内膨胀会导致壁板失效和依赖飞行轨迹的失效模式。高气动加热飞行方式(常马赫)导致静态应力失效，低气动加热率会导致突变跳跃现象。

(3)忽略结构变形对气动生热的影响，1%数量级的壁板长度的小位移可能导致10%数量级的壁板温度变化和100%数量级的壁板失效因子变化。

(4)马赫数以恒定速率上升的飞行状态下发生突变跳跃现象。且无论考不考虑变形导致的壁板压力变化都会有突变跳跃现象。但是，考虑变形导致的壁面压力会降低突变跳跃发生的时间。

参考文献：

[1] Dowell E H. Non-linear oscillations of a fluttering plate[J]. AIAA Journal, 1966,4(7):1 267-1 275.

[2] Dowell E H. Panel Flutter: A review of the aeroelastic stability of plates and shells[J].AIAA Journal, 1970,8(3):385-399.

[3] Cheng G F, Mei C. Finite element modal figuretion for hypersonic panel flutter analysis with thermal effects[J].AIAA Journal, 2003(35):1 517-1 530.

[4] Rogers M. Aerothermoelasticity[J].Aero/Space Engineering.,1958,17(10):34-43,64.

[5] Dechaumphai P. Fluid-Thermal-Structural Study of Aerodynamically Heated Leading Edges[J].Journal of Spacecraft and Rockets, 1989,26(4):201-209.

[6] Culler A J, Crowell A R, McNamara J J. Studies on fluid-structural coupling for aerothermoelasticity in hypersonic flow[J].AIAA Journal, 2009-2364, 2009.

[7] 杨超,李国曙,万志强.气动热-气动弹性双向耦合的高超声速曲面壁板颤振分析方法[J].中国科学,2012,42(4):369-377.

[8] 李国曙,万志强,杨超.高超声速翼面气动热与气动弹性综合分析[J].北京航空航天大学学报，2012,38(1):53-58.

(责任编辑：李华云)

Coupled Fluid-Thermal-Structural Modeling and Analysis of

Hypersonic Skin Panel

YANG Wu，HAN Jinglong

(College of Aerospace Engineering of NUAA， Nanjing Jiangsu210016， China)

Abstract：According to the fluid-thermal-structural coupling theory, a coupled model of three-dimensional panel in hypersonic airflow is established. The third-order piston theory is applied for the unsteady aerodynamics, the reference temperature method is used to compute the heating, and the finite element method is used for the heat transfer and structural deformation computation. Impacts of coupling types on response of the three-dimensional panel under different flight trajectory and structural boundary conditions are assessed. It is found that physical fluid-thermal-structural coupling mechanisms have much importance on response prediction of panel in hypersonic flow and the study is essential.

Keywords：hypersonic; aerothermoelasticity; three-order piston theory; two-way coupling; reference temperature method

作者简介：杨武(1990-)，男，江苏徐州人，硕士生，主要研究方向为气动弹性。

收稿日期：2014-11-26

中图分类号：V215.3

文献标识码：A

文章编号：1671-5322(2015)01-0028-06

doi:10.16018/j.cnki.cn32-1650/n.201501007