高斯束展开法的注记之三：辐射阻抗的简化计算*

2015-02-28袁迎春丁德胜

电子器件 2015年6期

袁迎春，丁德胜

（1.南京信息职业技术学院电子信息学院，南京 210023；2.东南大学电子科学与工程学院，南京 210096）

高斯束展开方法已广泛应用于快速计算菲涅尔场积分，即声场分布的计算。这种方法的实质是将菲涅尔场积分展开为一系列简单的基本函数的叠加，因而复杂的数值积分简化为一些简单函数（如Gaussian-Laguerre、Guassian-Hermite、高斯函数等）且项数不多的计算，计算量大为降低［1-6］。有关这一方法的详细描述可以参考综述文献［6］。

最近，我们给出高斯函数展开法的一种推广［7-11］。将文献中的圆形或矩形函数的高斯函数展开式或系数作为已知的结果，通过简单的数学变换，将贝塞尔函数和一阶Struve函数等特殊函数表示成高斯函数或其他简单函数的叠加。利用这一方法，给出了声学中一类圆形活塞声源的指向性函数以及均匀活塞的辐射阻抗函数的计算结果，与文献所给的相符合［9］。

本文将这种方法直接应用于一类圆形活塞声源辐射阻抗的计算，包括均匀分布、边缘简单支撑和边缘钳定的情形。所得结果与直接从特殊函数计算所得到的值相比，符合很好。本文是文献［9］研究结果的一种直接推广，作为我们一系列研究报告的第三部分。

1 辐射阻抗及其经典结果［12］

众所周知，辐射阻抗是声学中一个重要的参量，即由于声源振动，声辐射引起的附加于声源的力阻抗。在电声器件的设计中，除了要知道电声器件振动系统的力学参数如质量、弹性系数和力阻外，还必须知道由辐射声场对声源的反作用而产生的附加辐射阻和同振质量。

求声源的辐射阻抗，实际上即求声源振动时，媒质中的辐射声场对声源的反作用力。除了少数几种非常简单的声源，一般情况下，辐射阻抗的计算涉及到双重面积积分，通常是振荡型的积分。瑞利（Lord Rayleigh）采用十分巧妙的方法，将无穷刚性平面障板中圆形均匀振动活塞的辐射阻抗双重面积积分，简化成1阶贝塞尔（Bessel）函数和1阶斯特鲁夫（Struve）函数等特殊函数，已成为声学中的经典结果。

Greenspan推广了瑞利的经典结果，研究了活塞振动速度分布具有形式

的声场辐射问题［12］。为便于读者参考比较，我们尽量采用Greenspan的表述方式和记号。这里，r0为声源所在平面z=0上的径向坐标，即源点坐标，a是声源或辐射器的半径，V为声源的体积速度，即

n为一整数，H表示亥维赛阶跃函数。显然，n=0对应于均匀圆形活塞声源情形；n=1和n=2分别对应于最低阶的边缘（圆周r0=a处）简单支撑和边缘钳定活塞情形。当r0＞a时，由式（1）总是有v(r0)=0，这意味着活塞声源带有无限大刚性平面障板。

Greenspan研究的基本出发点乃是根据圆形轴对称时谐声场（随时间的变化关系为eiωt，ω是角频率）的King速度势公式。一旦求出声场的速度势，则相应的声场量，诸如声压、质点振速分布等皆可随之而得出。对于具有式（1）振速分布的声源，Greenspan得出声场在其表面的反作用力，表示为

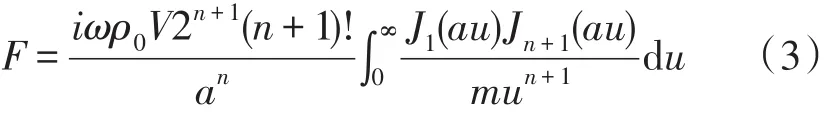
式中，时间因子eiωt已省略。ρ0是媒质（一般是空气）的密度，m=(u2-k2)12，波数k=ω/c，c为媒质的声速。公式（3）中以及下文出现的Jn(z)和Hn(z)分别代表第一类n阶贝塞尔（Bessel）函数和n阶斯特鲁夫（Struve）函数。Greenspan经过十分仔细而繁复的推导，得出了n=1，2，3时式（3）的显式表示，也就是，将上面的积分简化成几项Bessel函数和Struve函数。而将比值F/ρ0cV=R+iX，即归一化阻抗函数，化成这些特殊函数的计算。以下我们列出这些阻抗函数公式。

均匀圆形活塞（n=0）的归一化的阻函数为

这些近似公式可以作为本文计算正确与否以及计算精度的参照。

通常情况下，高于一阶的Struve函数一般不列表。Greenspan考虑到这一情况，将阻抗函数中出现的一阶以上的贝塞尔（Bessel）函数和斯特鲁夫（Struve）函数，全部化成零阶和一阶形式。实际上直到如今21世纪，一些常用的数学软件Matlab或Mathcad，以及FORTRAN和C等计算机语言软件包中，仍然不包括斯特鲁夫（Struve）函数的计算程序或库函数。

由于贝塞尔函数和斯特鲁夫函数在衍射理论中十分重要，而文献中有关这两种函数（特别是后者）的计算方法也不很多，所以我们给出贝塞尔函数Jn(z)和斯特鲁夫函数Hn(z)的一些近似高斯展开表达式，并用于阻抗函数的计算。

2 贝塞尔函数和斯特鲁夫函数的高斯展开式

Wen和Breazeale的一篇文章研究了圆形轴对称活塞声场分布的简化计算方法，即高斯束展开法［4-5］。这篇文章的一个附带结果表明：数学上，圆形函数

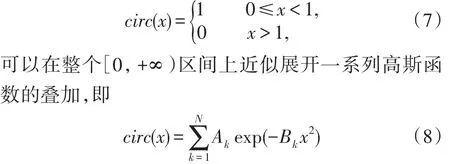
其中Ak和Bk称之为展开系数和高斯系数，可以用计算机最优化方法来求得。Wen和Breazeale给出了两组数据，其中一组10项的数据列在文献［4］的表1中；文献［13-14］给出了另外两组数据（项数稍多，精度稍高，一组25项［13］，一组 15项［14］）。这个近似展开式（8）在衍射理论中十分重要，可以简化许多复杂问题的分析和计算［15-20］。

以下我们将根据展开式（8），列出贝塞尔函数和斯特鲁夫（Struve）函数的高斯展开式。

零阶贝塞尔函数展开公式

公式（10）的导出，阶数ν要满足 Re(ν)＞1/2 的条件，因而直接从公式（10），取ν=0，得出 H0(x)的展开式，可能会有问题。利用递推公式

这里要注意的是，上列各公式中系数Ak和Bk与方程（8）为同一组数据。有关这些公式右边的展开精度，可以参考文献［7］。文献［7］中图2给出了一个比较［n=0 ，公式（9a）］。用10项高斯展开系数［4］计算，在大约0-20区间上，与J0符合很好，相对误差大约1%～2%。而另外一组15项的展开系数［5］在大约0～30的范围内，可以更好地拟合J0。上面这些公式的推导细节和和精度等的详细分析，这里就不给出了。

以下我们用这些特殊函数的近似展开式来计算圆形活塞阻抗函数。

3 计算过程与结果

这里我们给出均匀活塞（n=0）、边缘简单支撑（n=1）和边缘钳定这三种声源分布的辐射阻抗函数。最近杨某［14］给出了另外一组15项高斯展开系数，精度更高一些。以下计算中，主要用Wen和Breazeale的10项高斯展开系数［4］（第1组）和杨某［14］的这组数据（第2组），顺便比较一下精度。所用计算软件为Matlab 6.1。

对于均匀活塞情形，直接将贝塞尔函数和斯特鲁夫函数的展开式（10）等代入阻函数（4a）和抗函数公式（4b）中计算即可，图1给出了均匀活塞源归一化阻函数和抗函数的计算结果。

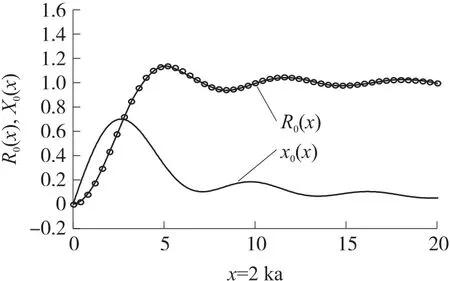
图1 均匀活塞（n=0）的辐射阻抗函数

图1中R0(2ka)分别采用近似展开（9b）和直接计算贝塞尔函数［Matlab中函数名为besselj（mu，x）］所得，两种方法所得结果颇相符合［第1组数据所得结果的最大绝对误差约9×10-3，第2组的最大误差约为5×10-4］。关于抗函数X0(2ka)，我们把根据（10a）式的计算结果，与课本中x=0(0.5)20的数值相比较，相对误差大约1%～2%［9］。

对于n=1，2的情况，编程计算时要有些技巧。将公式（10a）、（12）代入（5），即得简单支撑活塞的抗函数近似计算公式

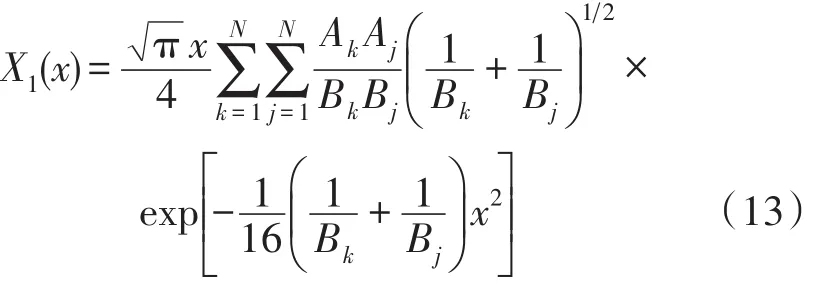
直接根据式（13）计算得到归一化抗函数曲线，如图2所示。对比Greenspan文献中图5，可见符合很好。但是，在计算阻函数R1过程中，出现了意外。我们把第1组数据［4］（Wen和Breazeale的10项系数）代入到式（5a）中，计算时发现：当x=2ka较大时（x约大于4），所得结果，与直接调用Matlab中的Bessel函数的计算结果，符合很好；而当x=2ka较小时，却完全不符。实际上当x很小时（接近于0，如取0.01），计算值是发散的。用第2组数据计算，同样有此错误。而根据阻抗函数的近似公式（5c），当x较小时，R1(x)≈x2/8。将公式（5b）改为如下形式后

情况变得十分明朗。原来问题出在上面式（14）的最后一项中。当J0(x)小近似展开后，最后一项中分子中的常数项应当为0。而将近似式（9a）代入（14）后，所得常数项δ=-1实际上并不等于零（这个值大致取决于（8）式的近似程度，第1组数据给出值约为-0.0127，第2组数约为0.011 5），那么式（14）主要计算误差由最后一项产生，也就是δ x2。若x=0.01，此时的误差就会被放大大约104倍。难怪计算结果发散!编程时，我们只需加上一些校正项，可以简单地消除这些误差，计算结果如图2所示。

图2 简单支撑活塞（n=1）的辐射阻抗函数

Greenspan实际上已经注意到类似的问题。也许他那个时代（1980年代），Bessel函数等特殊函数的计算精度不是太高，他的文章［12］中没有给出x＜1的那部分曲线。

采用类似的步骤，我们计算了边缘钳定活塞声源的辐射阻抗函数，如图3所示。计算过程中，我们利用贝塞尔函数和斯特鲁夫函数的递推公式，分别将式（6a）和（6b）改写成下面形式

采用这些表达式编程时，可以少加一些校正项。直接利用（6a）、（6b）式编程时，校正项可能要多一些，应当得出相同结果（或许消去的误差项更多，精度会更高一些）。读者不妨一试。

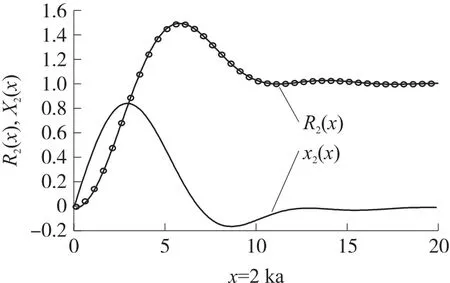
图3 边缘钳定活塞（n=2）的辐射阻抗函数

4 结语

我们给出了高斯函数展开法的推广，将圆形函数的高斯展开作为已知结果，通过简单的数学变换，将贝塞尔函数和Struve函数表示成高斯函数的近似和。计算了声学中一类活塞声源的辐射阻抗函数，与直接计算特殊函数的结果相比，我们的方法给出了相当一致的结果。这种方法还可以直接应用于活塞声源的辐射功率的计算。

最后我们指出，本文提供的这些例子，意味着现在的计算方法，可以作为特殊函数计算（精度要求不是太高）的补充。计算精度主要取决于方程（8）式的展开系数。作者希望我们的应用数学家给出具有更高精度的这类函数的高斯展开系数。此外，读者也许注意到，Bessel函数的高斯展开，如式（9），是单重级数形式，而Struve函数的展开是双重的形式。直观上，后者也应当有类似于式（9）的单重展开形式。有关Struve函数这方面的研究结果，我们将在不久的将来发表。

［1］Cook B D，Arnoult III W J.Gaussian-Laguerre/Hermite Formula⁃tion for the Nearfield of an Ultrasonic Transducer［J］.J Acoust Soc Amer，1976，59：9.

［2］Cavanagh E，Cook B D.Gaussian-Laguerre Description of Ultra⁃sonic Fields-Numerical Example：Circular Piston［J］.J Acoust Soc Amer，1980，67：1136.

［3］Thompson R B，Gray T A，J，et al.The radiation of Elliptical and Bicylindrically Focused Piston Transducers［J］.J Acoust Soc Am⁃er，1987，82：1818.

［4］Wen J J，Breazeale M A.A Diffraction Beam Field Expressed as the Superposition of Gaussian Beams［J］.J Acoust Soc Amer，1988，83：1752.

［5］Huang D，Breazeale M A.A Gaussian Finite-Element Method for Description of Sound Diffraction［J］.J Acoust Soc Am，1999，106：1771-1781.

［6］丁德胜，刘晓峻，黄锦煌.高斯束展开法在计算菲涅尔场积分中的应用，中国声学进展［M］.程建春，田静.北京：科学出版社，2008：55-68.

［7］Ding D S，Tong X J，He P Z.Supplementary Notes on the Gauss⁃ian Beam Expansion［J］.J Acoust Soc Am，2005，118：608.

［8］Dai Yurong，Ding Desheng.Further Notes on the Gaussian Beam Expansion［J］.Chinese Physics Letters，2012，29：024301.

［9］章力军，丁德胜.高斯束展开法的注记：指向性和辐射阻抗的简化计算［J］.电子器件，2013，36（6）：789-792.

［10］Ding D，Lu H，Shen C.A Novel Algorithm for the Sound Field of El⁃liptically Shaped Transducers［J］.Chin Phys Lett，2014，31：64301.

［11］鲍冬禺，丁德胜.高斯束展开法的注记之二：简单支撑矩形换能器声场［J］.电子器件，2015，38（2）：278-282.

［12］Greenspan M.Piston radiator：Some Extensions of the Theory［J］.J Acoust Soc Am，1979，65：608-621.

［13］Kim H J，Schmerr L W，Sedov A.Generation of the Basis Sets for Multi-Gaussian Ultrasonic Beam Models—An Overview［J］.J Acoust Soc Amer，2006，119：1971-1978.

［14］Liu W，Yang J.A Simple and Accurate Method for Calculating the Gaussian Beam Expansion Coefficients［J］.Chin Phys Lett，2010，27：124301.

［15］丁德胜，陆祖宏.活塞类声场的简化算法［J］.声学学报，1996，21（增刊）：421.

［16］Ding D S，Lu Z H.A Simplified Method to Calculate the Sound Field of Pistonlike Source［J］.Chin J Acoust，1996，15：213.

［17］Ding D S，Liu X J.Approximate Description for Bessel，Bessel-Gauss and Gaussian Beams with Finite Aperture［J］.J Opt Soc Amer，1999，A 16：1286.

［18］Zhang Y，Liu J Q，Ding D S.Sound Field Calculations of Ellipti⁃cal Pistons by the Superposition of Two-Dimensional Gaussian Beams［J］.Chin Phys Lett，2002，19：1825.

［19］Ding D S，Zhang Y.A Simple Calculation Approach for the Sec⁃ond-Harmonic Sound Beam Generated by an Arbitrary Distribu⁃tion Source［J］.Chin Phys Lett，2004，21：503.

［20］谢晓霞，王硕琛，吴逢铁.Bessel光束经椭圆环形孔径后的衍射光场［J］.物理学报，2015，64（12）：124201.