不同蒸散发模型在大凌河流域的对比运用研究

李 非

（辽宁省水文局，辽宁 沈阳 110003）

1 引 言

蒸散发是水文循环的重要组成部分，如何定量估算流域的蒸散发一直是国内外学者研究的重要课题，也取得了许多的运用成果,但不同蒸散发模型在不同流域都具有一定的适用性，而蒸散发量的正确估算对于水文模拟至关重要，特别是在无资料地区的水文模拟，由于缺少实测蒸发皿数据，蒸散发只能通过蒸散发模型来进行有效的估算，不同蒸散发模型在不同流域其估算精度不同，且需求的数据也不同，因此应结合流域实际情况，选择在流域具有适用性好的蒸散发模型。本文以大凌河流域作为研究区域，该区域处于东亚季风区与西北干旱非季风区迂回区域，使得流域多年平均蒸发量高于降水4.5倍。因此此文以大凌河大城子水文站以上为研究流域，将如今运用较为广泛的双源蒸散发模型和P-M公式在研究流域进行对比分析，分析两个蒸散发模型在大凌河流域的适用性，并结合流域内气象要素数据和实测蒸发皿数据，定量分析气象要素变化对蒸发皿蒸发的影响，研究成果对于大凌河流域蒸散发的估算和水资源评价提供重要的参考价值。

2 研究方法及研究区域概况

分别运用双源蒸散发模型和P-M计算大凌河大城子以上流域蒸散发，收集了流域内朝阳气象站1964—2000年的日观测数据，气象数据包括平均水汽压、平均气温、最高气温、最低气温、平均风速、日照时间及辐射资料等。

2.1 双源蒸散发模型

双源蒸散发模型将植被和土壤考虑成2个单独的蒸发源，分别建立植被和土壤蒸发模型，模型的具体原理，考虑文章篇幅，参见《双源蒸散发模型估算潜在蒸散发量的对比》等相关文献。

2.2 P-M公式

P-M公式是由联合国粮农组织（FAO）推荐使用的参考作物蒸发蒸腾量计算公式，具有较好通用性。计算公式：

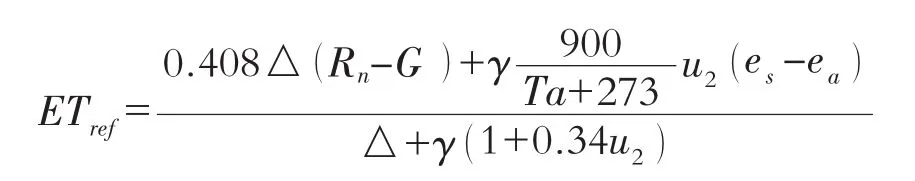
其中：ETref表示参考作物蒸散量，mm/d；△表示饱和水汽压—温度曲线上的斜率 ，kPa/℃；Rn表示太阳净辐射，MJ/m2；G 表示土壤热通量，MJ/（m2·d）；γ表示空气湿度常数，kPa/℃；Ta表示空气平均气温 ，℃；u2表示 2 m处平均风速，m/s；es表示饱和水汽压 ，kPa；ea表示温度时水汽压 ，kPa。

2.3 研究区域概况

大凌河全长397 km，是辽宁省西部最大的河流,流域面积2.35×104km2，流域内年降水量450～600 mm，流域降水量主要集中7、8两个月份。流域年均径流量16.67×108m3，流域多年平均蒸发量为。此文选取大凌河上游大城子水文站作为研究区域，研究区集水面积为5029 km2，研究流域内共有16个降雨站点。

3 不同蒸散发模型计算结果对比研究

3.1 年尺度分析

基于朝阳气象站1964—2000年的实测观测气象数据级流域叶面积指数数据，运用双源蒸散发模型和P-M公式计算流域年蒸散发，并结合大城子站1964—2000年实测蒸发皿蒸发资料，定量分析了计算蒸散发和实测蒸散发的相关性，具体结果，见图1，2。

图2为运用双源蒸散发模型和P-M公式计算的蒸散发及实测蒸发皿1964-2000年蒸散发年变化趋势图，从图中可以看出，两种蒸散发模型计算的年蒸散发均呈现下降趋势，其M-K统计值分别为-2.09（P-M 公式）和-2.258（ 双源蒸散发模型），均通过了置信度为95%的显著性检验，这和大城子站实测蒸发皿蒸散发变化趋势是一致的，实测蒸发皿蒸发M-K统计值为-3.68。绘制为PM公式和双源蒸散发模型与实测蒸发皿之间的相关图，可知，P-M公式与实测蒸发皿蒸发的相关性为0.36，双源蒸散发模型与实测蒸发皿蒸发相关性为0.42，可见，双源蒸散发模型与实测蒸发皿蒸发具有更好的相关性。

3.2 月尺度分析

在年尺度分析的基础上，考虑到月蒸发分布的影响，统计分析了双源蒸散发模型、P-M公式以及实测蒸发皿月尺度蒸散发变化，结果见图3和表1。

绘制实测蒸发皿和双源蒸散发以及P-M公式计算的月蒸散发对比图，可以看出，2个模型计算的月蒸散发和实测蒸发皿蒸发在过程上具有较好的吻合度，7—9月份为大凌河流域蒸发量最大的几个月份。表1为统计的P-M公式以及双源蒸散发模型和实测蒸发皿蒸发之间观测值的比较，从表中可以看出，双源蒸散发与观测值较为接近，且双源蒸散发计算值大于P-M蒸散发计算的蒸散发值，这主要是因为双源蒸散发考虑了土壤和植被的蒸散发，而P-M公式未考虑植被蒸散发的影响，因此双源蒸散发计算值比P-M公式计算值大。

4 不同气象要素与蒸发皿蒸发的相关性分析

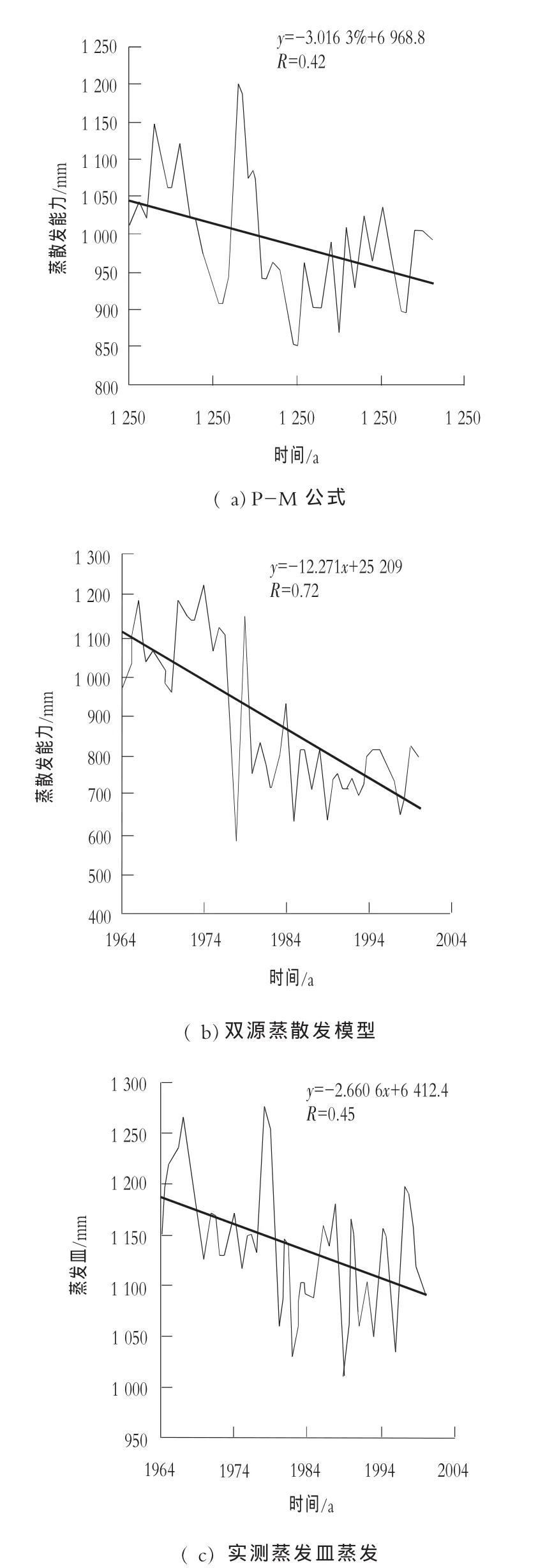
图1 P-M公式、双源蒸散发计算模型及实测蒸发皿蒸发多年变化趋势的比较

基于朝阳气象站1964—2000年气象要素数据，采用反距离加权平均方法将朝阳站气象数据插值到大城子水文站所在位置的气象数据，定量分析了不同气象要素对实测蒸发皿蒸散发的影响。

图2 P-M公式、双源蒸散发模型与观测值相关关系

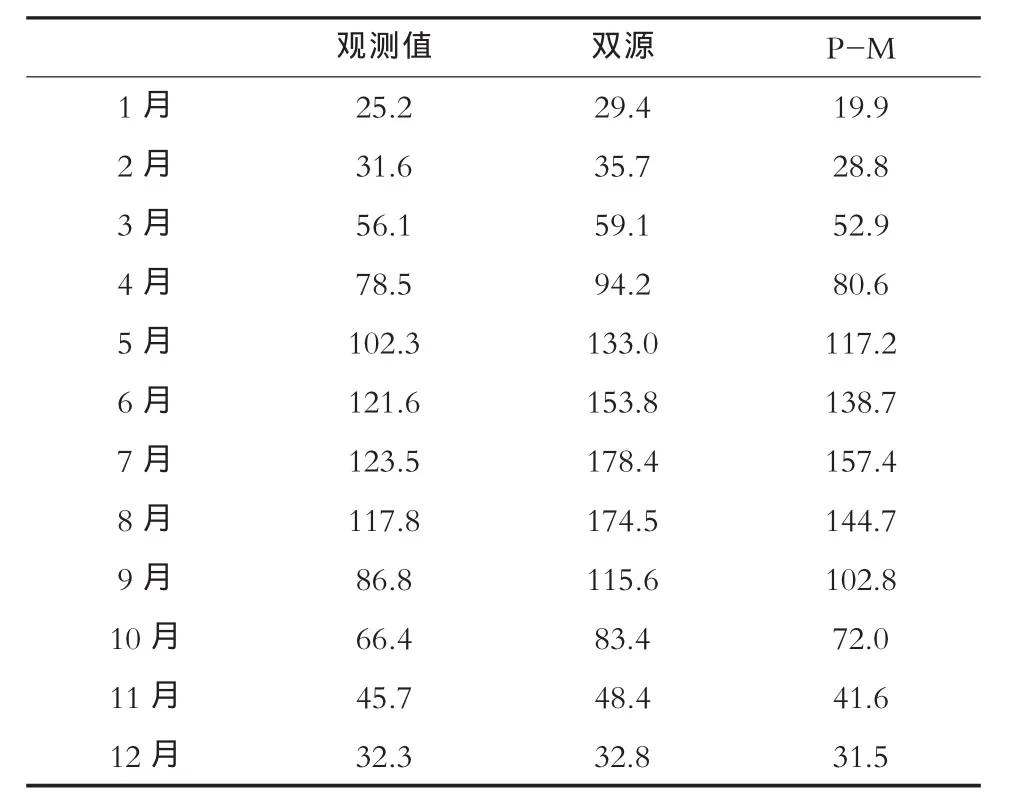
表1 P-M公式、双源蒸散发计算模型与蒸发皿观测值的比较mm

图3为大凌河流域年实测蒸发皿蒸发与各气象要素之间相关关系，从图中可以看出大凌河流域年蒸散发与气温、相对湿度、风速以及净幅射相关系数分别为-0.28，072，0.22以及0.2，可见相对湿度与实测蒸发皿相关性最高，其次是气温和风速，净幅射相关性最弱。

5 结 论

运用双源蒸散发模型和P-M公式分别计算了大凌河流域的蒸散发，并与实测蒸发皿蒸发进行了对比分析，在此基础上，定量分析了不同气象要素和实测蒸发皿蒸发之间的相关性，研究取得以下结论：

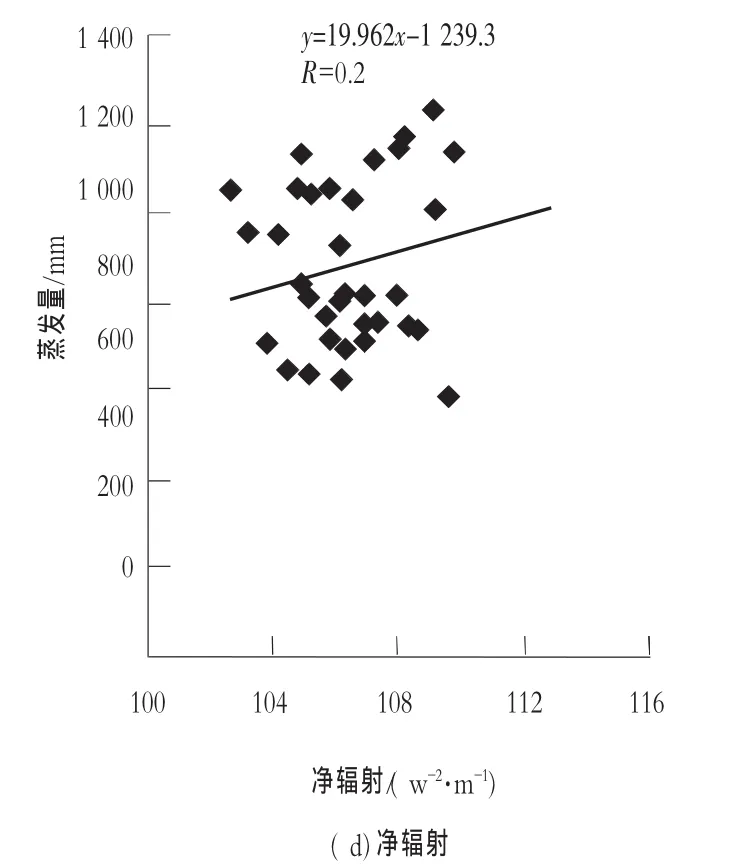
图3 大凌河流域年尺度蒸发皿蒸发与各气象要素相关关系

1）双源蒸散发模型和P-M公式计算的蒸散发和实测蒸发皿蒸发都较为吻合，两个模型中，双源蒸散发模型计算的蒸散发在年尺度和月尺度上与实测蒸发皿蒸发相关性均最高，双源蒸散发模型更适合于大凌河流域的蒸散发计算；

2）相对湿度与实测蒸发皿蒸发的相关性最高，其次是气温和风速，净幅射相关性最低。

［1］李修仓.中国典型流域实际蒸散发的时空变异研究［D］.南京信息工程大学，2013.

［2］王任超，张利平，徐霞.南水北调中线工程水源区蒸散发计算方法比较及影响因素分析［J］.长江流域资源与环境，2012，S1：127-133.

［3］秦年秀，陈喜,薛显武,凌敏华,张志才.潜在蒸散发量计算公式在贵州省适用性分析［J］.水科学进展，2010（3）：357-363.

［4］刘波，翟建青，高超，姜彤，王艳君.基于实测资料对日蒸散发估算模型的比较［J］.地球科学进展，2010（ 9）：974-980.

［5］张士锋，王翠翠，孟秀敬，华东，门宝辉，李智飞.永定河北京段蒸散发研究［J］.地理科学进展，2013（ 04）：580-586.

［6］刘晓帆，任立良，袁飞，徐静.双源蒸散发能力计算模型在半干旱区的适用性［J］.河海大学学报(自然科学版)，2009（ 2） ：138-142.

［7］王声锋，段爱旺，张展羽.半干旱地区不同水文年Hargreaves和 P-M 公式的对比分析［J］.农业工程学报，2008（7）：29-33.

［8］杨雨亭，尚松浩.双源蒸散发模型估算潜在蒸散发量的对比［J］.农业工程学报，2012（ 24）：85-91.