改进的垂向混合产流模型在大凌河流域的运用

2015-02-28闻绍珂

东北水利水电 2015年4期

闻绍珂，蔡涛

（辽宁省水文局，辽宁沈阳 110003）

1 引言

垂向混合产流模型在北方地区流域取得了不错的运用效果,但是传统垂向混合产流模型在河道汇流演算时将槽蓄系数设置为固定值，不能考虑河段槽蓄系数的差异性的缺点，引入变动态存储系数法对河道汇水演算进行改进，动态考虑河段槽蓄系数的变化，并将改进的垂向混合产流模型和传统垂向混合产流模型进行对比分析。计算时段的长短对于水文模拟的影响近些年来得到广泛学者的研究和关注，在大凌河流域的洪水模拟中，计算时段常常取为1 h,对于更短计算时段的洪水模拟研究较少，而次洪模拟精度对于大凌河流域的防洪模拟至关重要。因此，基于改进的垂向混合产流模型，分别模拟计算时段为0.5 h和1 h的次洪模拟，对比分析不同计算时段对次洪模拟的影响。此外，考虑到无资料地区水文模拟无实测蒸发资料，但有实测的气象资料，而通过实测气象资料，可计算流域的蒸散发。因此对比计算的蒸散发和实测蒸散发对水文模拟的影响，来定量分析计算的蒸散发是否可替代实则蒸散发用于大凌河流域无资料地区的水文模拟，研究成果对于大凌河流域水文模拟提供重要的参考价值。

2 研究方法及研究区域概况

2.1 研究区域概况

大凌河全长397 km，是辽宁省西部最大的河流，流域面积2.35×104 km2，流域内年降水量450～600 mm，流域降水量主要集中7、8两个月份。流域年均径流量16.67×108m3，本文选取大凌河上游大城子水文站作为研究区域，研究区集水面积为5029 km2，研究流域内共有16个降雨站点。

2.2 研究方法

对传统垂向混合产流在河道汇流演算进行改进，对于垂向混合产流模型，研究成果较多，考虑到文章篇幅原因，垂向混合产流模型的原理可详见参考文献。而在不同蒸发输入对水文模拟影响时，蒸散发计算采用P-M公式，P-M公式的具体原理也可详见参考文献[7]，本文着重介绍考虑河道槽蓄系数动态变化的变动态存储系数法，该方法原理如下：

该方法槽蓄方程计算公式：

式中：I表示时段初流入河段的流量，m3/s；Q表示时段末流出河段的流量，m3/s；W表示河段内蓄水量，m3；Q’代表演算流量，m3/s，Q’=xI+(1-x)Q； x表示流量的一个比重系数，K表示蓄量与流量关系曲线的一个斜率，h。

斜率K值和河段长度以及洪水波波速相关，计算的公式：

式中：L表示河段长度，m；Vc表示是洪水波的波速，m/s。

对于河流断面形状能近似为宽矩形的河段，其洪水波传播的速度可采用学者Schulze提出的方法进行计算，计算原理如下所示：

式中：V为河流的平均流速，m/s。

而河流的平均流速可选用曼宁公式进行计算，计算方法：

式中：R表示水力半径，i表示河道平均比降，‰，n表示河段的糙率。

2.3 研究资料

此文收集了大凌河流域大城子水文站2001—2010年日流量及蒸发数据，大城子以上2000—2010年降雨数据，并收集了大城子水文站2001—2010年15场次洪数据；气象数据，收集了流域附近朝阳气象站2001—2010年气象数据，气象数据包括：最高最低气温，相对湿度，风速，太阳辐射。

3 成果分析

3.1 两种水文模型模拟精度的对比分析

分别运用改进垂向混合产流模型和传统垂向混合模拟了大凌河流域2000—2010年日径流，模拟成果见表1和图1。

表1为两站水文模型模拟结果对比图，从表1中可以看出，改进的垂向混合产流模型和传统垂

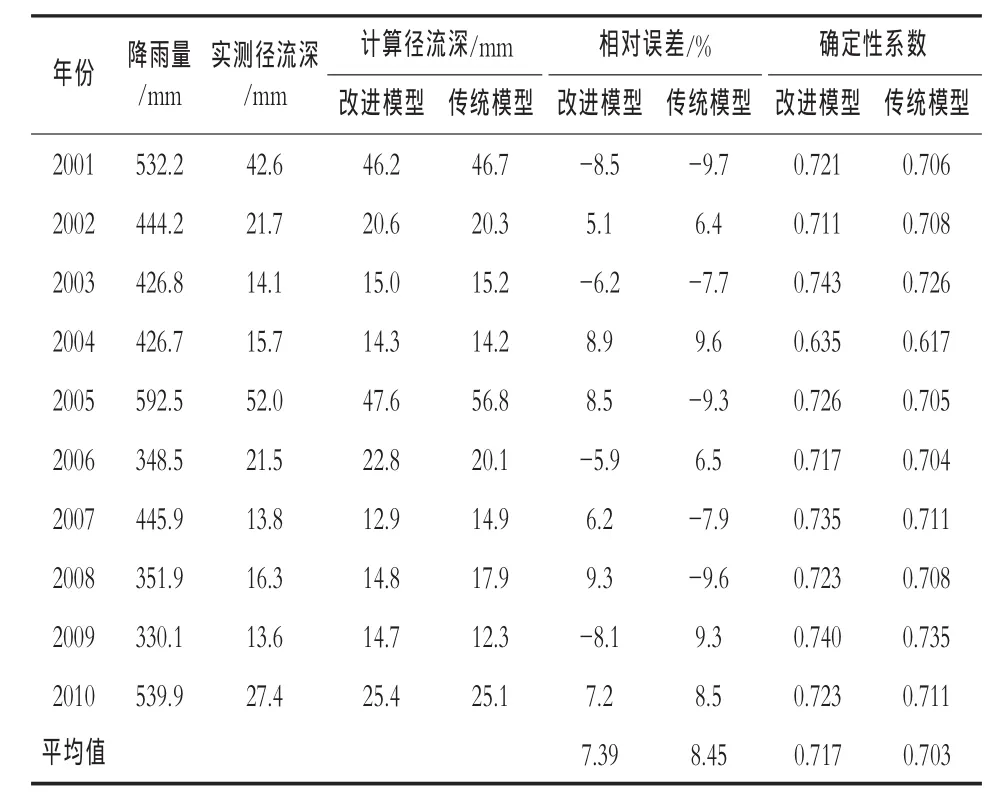
表1 改进的垂向混合产流模型与传统垂向混合产流模型模拟对比结果

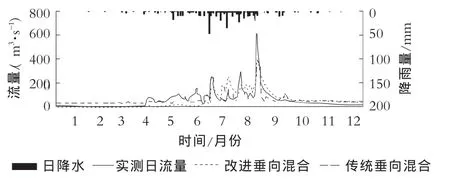
图1 2001年两种水文模型模拟结果对比图

向混合模型模拟的结果都可以满足模型模拟的精度要求，两种水文模型在2000—2010年模拟的相对误差均在10%以内，确定性系数都在0.7以上，可以满足大凌河流域水文模拟的精度要求，改进的垂向混合产流模型和传统垂向混合模型均可适用于大凌河流域的水文模拟。从两种水文模型模拟的精度来看，改进的垂向混合产流模型在2001—2010年模拟的径流深相对误差的平均值为7.39%，而传统垂向混合模型模拟的径流深相对误差的平均值为8.45%。可见在径流深相对误差方面，改进的垂向混合产流模型好于传统垂向混合模型。确定性系数表示水文模型在过程模拟的好坏，从表1中可以看出，两种水文模型模拟的确定性系数都达到了0.7以上，可以说两种水文模型在过程上都具有较好的模拟精度，相比而言，垂向混合产流模型在2001—2010年模拟的确定性系数平均值为0.717，而传统垂向混合产流模型模拟的确定性系数平均值为0.703，可见，改进的垂向混合产流模型在过程上的拟合度方面也要好于传统垂向混合产流模型。这一点也可从图1中看出，图1为两种水文模型在2001年的模拟过程对比图，从图1中可以看出，两种水文模型都具有较好的拟合度，改进的垂向混合产流模型在过程要好于传统垂向混合产流模型。

3.2 不同计算时段对水文模拟的影响分析

选用改进的垂向混合产流模型定量分析不同计算时段对水文模拟的影响,基于大城子水文站2001—2010年15场洪水分别分析计算时段为0.5 h和1 h对水文模拟精度的影响，模拟结果，见表2。

表2 不同时段对水文模拟的影响对比结果

表2为不同计算时段对改进的垂向混合产流模型的模拟结果对比，从表2中可以看出，计算时段为0.5 h的水文模拟精度要好于计算时段为1 h的水文模拟精度，在2001—2010年15场洪水中，1 h模拟的径流深相对误差的平均值为1.37，0.5 h模拟的径流深平均相对误差为1.45，可见在径流深相对误差方面，时段越短模拟的径流深相对误差越小，而水量模拟的精度高低对于次洪模拟至关重要，在15场洪水中，计算时段为0.5 h模拟的径流深相对误差也均小于计算时段为1 h模拟的径流深相对误差。在峰现时间上，同样可以看出，计算时段为1 h模拟的峰现时间差平均值为-0.5 h，而0.5 h模拟的峰现时间差平均值为-0.47 h，在峰现时间上，计算时段为0.5 h的模拟精度也要好于计算时段为1 h的模拟精度。在确定性系数上，计算时段为0.5 h模拟的确定性系数平均值为0.652，好于计算时段为1 h模拟的确定性系数，表明在次洪过程模拟方面，计算时间越短，模拟过程越为吻合。

3.3 不同蒸发输入对水文模拟的影响分析

为量分析不同蒸发输入对水文模拟的影响，分别选用P-M公式计算蒸发，并和实测蒸发皿蒸发作为模型蒸发输入，对比分析不同蒸发输入对水文模拟的影响。选用大城子水文站2001—2010年水文资料，计算结果见表3。

表3 不同蒸发输入对水文模拟的影响对比结果

表3为不同蒸发输入对水文模拟的影响对比结果，从表3中可以看出，运用P-M蒸散发模型作为蒸散发输入模拟的径流深平均相对误差为6.78%，而实测蒸发皿蒸发作为输入的模拟径流深相对误差为7.39%，可以看出，P-M蒸散发模型作为蒸发输入在径流深相对误差方面精度有所提高，这主要是因为P-M蒸散发将土壤和植被都作为蒸发源进行单独计算，而蒸发皿蒸发只是考虑水面蒸发。从两种蒸发输入模拟的确定性系数来看，PM蒸散发输入的平均确定性系数为0.720，实测蒸发皿蒸发模拟的平均确定性系数为0.717，同样，P-M发作为蒸发输入模拟的确定性系数要好于运用实测蒸发皿蒸发模拟的平均确定性系数。