具Logistic增长项的极小趋化系统的稳定性分析
2015-02-28李忠芳韩亚洲
李忠芳,韩亚洲
(中国计量学院 理学院,浙江 杭州 310018)

具Logistic增长项的极小趋化系统的稳定性分析
李忠芳,韩亚洲
(中国计量学院 理学院,浙江 杭州 310018)
利用扰动分析给出极小趋化系统的线性化系统,然后通过分析各个模态的振幅的长时间行为给出常数定态解的稳定性分析.发现平凡定态解总是不稳定,非平凡常数定态解的稳定性依赖于趋化系数,即当趋敏效应较强时,所有常数定态解都不稳定,从而预测了非常数定态解的存在性.最后结合数值实例,验证了理论分析的结果,且预测了非常数定态解的稳定性.
极小趋化系统;常数定态解;稳定性分析;数值仿真
近代以来,采用模型研究和数值计算相结合的方法,大大推动了生物模型的理论分析,为生物实验提供了理论依据[1].本文主要研究一类具有趋敏运动的生化趋化模型,以揭示趋敏效应在斑图现象中的作用.
1970年,Keller和Segel[2]提出了经典的趋化模型
(1)
它描述了单细胞生物阿米巴受自身分泌的化学物质吸引聚集的现象,其中u,v分别表示细胞和化学物质的密度,增长项f(u,v)表示细胞本身分泌化学物质,所以这种聚集现象(一种斑图解)是一种自组织的过程.1981年,Childress和Perkus[3]对模型(1)进行简化,取D1,Dv为正常数,k(v)=α,f(u,v)=βu,D2=χu,其中α,β,χ(趋化系数)均为正常数,即模型(1)化为
(2)
我们称该模型为极小系统.之后,许多学者对极小系统的一些有趣性质进行研究,如:在一维空间中,Osaki和Yagi[4]研究了极小系统解的全局存在性;而Horstmann[5]则对1970年到2003年之间关于极小系统解的爆破行为的研究进行了总结;对极小系统更多的研究介绍可参看文献[6-8]等.最近,Wang和Xu[9]研究了包括模型(2)在内的六类趋化模型,特别证明(2)存在斑图解(稳定的非常数定态解),第一个分支为全局分支,且进一步证明:当χ/d1→∞时,斑图解趋向于聚点解(爆破解).
模型(1)、(2)均假设时间很短,细胞没有增长,故关于细胞密度u的控制方程中没有反应项.而文献[10-11]则对一类带有细胞增长项的生化趋化模型,讨论解的稳定性问题.因此,本文拟考虑具有Logistic增长项的极小趋化系统模型,具体如下:
(3)
式(3)中:(x,t)∈Ω×(0,+∞),Ω—RN中带有光滑边界∂Ω的有界域,本文主要研究一维问题,故取Ω=[0,l];u(x,t)和v(x,t)—细胞密度和化学物质的浓度;d1>0—细胞的扩散系数,d2>0—化学扩散系数;χ>0为趋化系数,它反映了化学趋化响应强度;μu(1-u/uc)描述细胞具有增长率为μ>0、运载能力为uc(0
取模型的初始条件为
u(x,0)=u0(x),v(x,0)=v0(x),x∈[0,l].
(4)
边界条件为Neumann边界条件,即
(5)
本文安排如下:第一节利用扰动分析法,分析常数定态解的稳定性;且证明平凡解总不稳定,而对非平凡常数定态解,存在临界趋敏系数χc(定义见(18)),当χ<χc时稳定,当χ>χc时不稳定;从而预测了非常数定态解的存在性.在第二节,结合具体例子进行数值仿真,发现数值结果与理论分析结果一致,进一步验证了理论分析的有效性,并给出稳定非常数定态解存在的例子.最后在第三节,总结全文并提出进一步的问题讨论.
1 常数定态解的稳定性分析

1.1 平凡定态解(0,0)的稳定性分析
令u=0+U,v=0+V,其中U,V为平凡定态解(0,0)的一个小扰动,代入极小趋化系统,可得如下线性化系统
(6)

在Neumann边界条件下,设
(7)
代入线性化系统,解之得:
(8)
(9)
注意到μ>0,所以当t→+∞时,第一个模态的振幅eμt→∞.故有如下结论:
结论1 若μ>0,则常数定态解(0,0)是不稳定的.
生物解释 若细胞满足Logistic增长率,则不会趋于灭绝.


(10)
如2.1节的讨论,稳定性的研究主要在于各模态的稳定性,故直接设
(11)
代入线性化系统有A(rn,sn)T=0,其中
(12)
则存在非平凡解的充要条件为|A|=0,从而λn满足色散关系
(13)
其中
(14)
(15)
解(13)得
(16)

记
f(k2)=(d1k2+μ)(d2k2+α)-χucβk2=d1d2k4+qk2+μα,
其中q=μd2+αd1-χucβ,则f(k2)开口向上,且
令
则当χ=χc时,fmin=0;当χ<χc时,fmin>0;当χ>χc时,fmin<0.
综合上述分析,有

(19)

(20)
为f(k2)=0的两个正根.

2 数值仿真与非常数定态解的稳定性
在系统(3)~(5)中,选取参数为:d1=0.1,d2=0.8,μ=0.5,uc=0.2,β=16,α=12,l=2π,则χc≈0.933.下面将利用Matlab语言中提供的pdepe函数对系统(3)~(5)进行仿真,以进一步验证第二节的理论分析结果.


图1 l=2π,常数定态解(0,0)加扰动后的长时间行为Figure 1 Long time behavior of (0,0) with small perturbation for l=2π

图2 l=2π,χ=1>χc,常数定态解加扰动后的长时间行为

图3 l=2π,χ=0.48<χc,常数定态解加扰动后的长时间行为

定模态有n=5,6,7;当l=4π时,不稳定模态有n=9,10,11,12,13,14,15.
最后,我们给出如下的仿真实例:取区间足够的大,一个局部的扰动会怎么样呢?在图5中,取l=60,χ=1.2>χc,其余参数如图2,然后在左端点给定一个小扰动.如图5,小扰动首先形成一个局部的斑图,然后逐渐的入侵至整个区间.
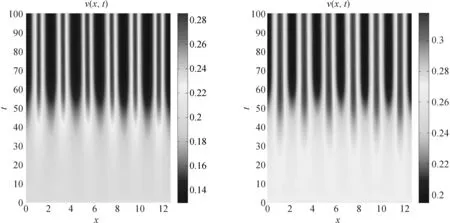
图4 l=4π,χ=1>χc,常数定态解加扰动后的长时间行为

图5 l=60,χ=1.2>χc,常数定态解附近的局部扰动引起的入侵现象
3 总结和展望
当χ>χc时,两个常数定态解都不稳定,那么在长时间行为下,解极限是什么呢?是否如第二节的仿真结果一定趋向于斑图解呢?这些将是本文后续的主要研究问题.
另外,如第二节中数值例子,当l=2π或l=4π时,系统出现多个不稳定模态,那么经过长时间运行后,是趋向于某个不稳定模态,还是多个不稳定模态共存呢?哪个不稳定模态最不稳定呢?这个问题对生态现象的预测非常重要,这也是我们要继续研究的问题.
[1] 吴秀山,侯宇,李希靖.强激光作用下生物组织热损伤问题的研究[J].中国计量学院学报,2002,13(2):135-138. WU Xiushan, HOU Yu, LI Xijing. The research on thermal damage in biological tissues induced by high-irradiance-laser[J].Journal of China University of Metrology,2002,13(2):135-138.[2] KELLER E, SEGEL L. Initiation of slime mold aggregation viewed as an instability[J].Journal of Theoretical Biology,1970,26(3):399-415.
[3] CHILDRESS S, PERKUS J. Nonlinear aspects of chemotaxis[J].Mathematical Biosciences,1981,56:217-237.
[4] OSAKI K, YAGI A. Finite dimensional attractor for one-dimensional Keller-Segel equations[J].Funkcialaj Ekvacioj,2001,44(3):441-469.
[5] HORSTMANN D. From 1970 until present: the Keller-Segel model in chemotaxis and its consequences I[J].Jahresbericht der DMV,2003,105(3):103-165.
[6] PERTHAME B. Transport Equations in Biology[M].Basel: Birkhäuser,2007:113-138.
[7] SUZUKI T. Free Energy and Self-Interacting Particles[M].Boston: Birkhäuser,2005:221-248
[8] HILLEN T, PAINTER K J. A user’s guide to PDE models for chemotaxis[J].Journal of Mathematical Biology,2009,58:183-217
[9] WANG X, XU Q. Spiky and transition layer steady states of chemotaxis systems via global bifurcation and Helly’s compactness theorem[J].Journal of Mathematical Biology,2013,66(6):1241-1266.
[10] MA Manjun, HU Jiajia, TAO Jicheng, et al.Non-existence of stationary pattern of a chemotaxis model with logistic growth[J].Nonlinear Analysis,2014,105:3-9.
[11] MA Manjun, OU Chunhua, WANG Zhian. Stationary solutions of a volume-filling chemotaxis model with logistic growth and their stability[J].Society for Industrial and Applied Mathematics,2012,72(3):740-766.
Stability analysis of a minimal chemotaxis model with logistic growth
LI Zhongfang, HAN Yazhou
(College of Sciences, China Jiliang University, Hangzhou 310018, China)
Using perturbation analysis we obtained the linearized system of the minimal chemotaxis system.Then we analyzed the stability of constant steady-state solutions by studying the long-time behavior of the amplitude of each mode.It was found that the trivial solution was unstable and the non-trivial constant solution chemotactic coefficient played the key role.When the chemotactic effect was stronger,all constant solutions were unstable.It suggested the existence of non-constant steady-state solutions. Finally, numerical examples testified the theoretical results and predicted the stability of non-constant steady-state solutions.
minimal chemotaxis model; constant steady-state solution; stability analysis; numerical simulation
1004-1540(2015)04-0495-06
10.3969/j.issn.1004-1540.2015.04.019
2015-06-23 《中国计量学院学报》网址:zgjl.cbpt.cnki.net
国家自然科学基金资助项目(No.11201443,11271342).

O193
A
