基于倾侧角反馈控制的预测校正再入制导方法

赵江，周锐

(北京航空航天大学自动化科学与电气工程学院，北京100191)

0 引言

高超声速飞行器再入滑翔制导性能受到了大气模型参数的不确定性和动力学系统的强扰动性等诸多因素的制约，已经成为各国航空航天领域研究的重点问题和难点问题［1-3］。再入制导方法通常分为标准轨迹制导和预测校正制导两大类。标准轨迹制导方法通过设计导引律以实时跟踪事先确定的标准再入轨迹，对弹载计算机的性能要求比较低，但是较大的初始轨迹偏差可能会导致制导性能严重退化。预测校正制导方法则是通过预测再入飞行器的落点位置偏差来对制导指令进行实时修正，能够显著降低初始散布误差对制导性能的影响，提高制导精度。因此，预测校正制导成为高超声速飞行器再入滑翔制导方法的发展趋势［4-5］。

文献［6］利用准平衡滑翔特性设计了一种简单可行的预测校正制导方法，该方法将再入滑翔飞行中的过程约束转化为倾侧角的边界约束，通过对运动方程进行数值积分来预测飞行器的待飞航程误差，实时校正倾侧角控制指令。在此基础上，文献［7 -8］提出了分段的预测校正制导方法，进一步提高了落点预测精度和迭代计算效率。文献［9 -10］则以能量为自变量建立三自由度运动学方程，通过求解待飞航程误差与能量的近似关系，分别设计纵向制导律和侧向制导律，增强了预测校正制导方法的灵活性。文献［11 -13］分析了大气模型的不确定性和气动参数偏差对落点预测的影响，在预测校正制导中引入了参数估计和修正环节，提高了再入制导算法的适应性。文献［14 -15］在标准轨迹制导和预测校正制导的基础上提出了混合再入制导方法，通过设计误差补偿策略和算法切换机制，将再入制导归纳为最优化求解问题，增强了再入制导的抗干扰能力。

为了抑制再入滑翔轨迹的周期性震荡现象，上述预测校正制导方法都必须利用准平衡滑翔条件(QEGC)对制导指令进行修正。然而，在飞行航迹角增大或轨道再入速度较低等特殊情况下，QEGC有可能失效［16］。因此，不能完全依赖于该条件进行再入制导律设计。

本文在预测校正制导方法的基础上，对升力式高超声速飞行器的再入制导问题进行了研究，提出了一种能够有效抑制周期性轨迹震荡的滑翔制导律。

1 再入制导问题

1.1 三自由度运动学方程

高超声速飞行器的控制问题通常采用六自由度模型来描述再入飞行特性，其结构较为复杂且主要用于姿态回路的控制律设计。本文主要研究再入滑翔制导律设计，即外环回路制导律设计问题。因此，忽略再入飞行过程中风速和向心力影响的前提下［17］，建立如下高超声速再入飞行器的三自由度无量纲运动方程［18］

式中:r 为无量纲地心距;V 为飞行器相对地球的无量纲速度;θ 和φ 分别为经度和纬度;γ 和ψ 分别为飞行航迹角和航向角;Ω 为地球的自转角速度;σ 为飞行器的倾侧角;L 和D 分别为无量纲的升力加速度和阻力加速度，具体计算公式为

式中:KC= 0.5R0Sref/ m;ρ 为大气密度;CL和CD分别为升力系数和阻力系数;R0为地球半径;Sref为飞行器参考面积;m 为飞行器质量。

1.2 再入过程约束

高超滑翔飞行器的再入飞行过程主要考虑热流密度约束Q、动压约束q 和过载约束n 的影响，具体计算公式如下所示［19］:

式中:KQ为与飞行器相关的常值参数;g0为海平面地球引力加速度;Qmax、qmax和nmax分别为热流密度约束、动压约束和过载约束的最大幅值，由高超声速飞行器本身的结构和材料所决定。约束(3)式～(5)式为再入滑翔飞行过程中必须满足的硬约束条件。

1.3 再入终端约束

不失一般性，引入如下能量形式的e 作为自变量:

本文考虑的再入飞行终端约束主要包括终端高度约束、终端速度约束和终端经度与纬度约束，表达形式为

式中:rf、Vf、θf和φf分别为再入滑翔飞行器地心距、飞行速度、经度和纬度的给定终端状态。

2 预测校正制导

2.1 纵向制导律设计

考虑到再入飞行器初始下降段的热保护要求，纵向制导设计采用升力式滑翔制导常用的二次函数分段标称攻角剖面，具体计算公式为

式中:α0为再入攻角初值:VT为飞行器攻角幅值开始下降时的临界速度:K 为常值参数。

通过对热流密度约束、动压约束和过载约束进行转化，在高度-速度平面建立再入飞行走廊的下边界，可以得到飞行器控制倾侧角的幅值约束，表达形式［20］为

即过程约束下倾侧角的最大幅值为

高超声速飞行器的再入高度较高，导致初始下降段的气动力较小，因此该段主要采用开环制导方式。本文选择常值倾侧角σ0作为初始下降段的控制变量，其具体计算公式为

式中:ψT为再入初始状态的目标视线角;Δψ 为航向角误差。

再入飞行器下降飞行过程中，高度轨迹震荡的最大幅值通常出现在第一个波谷之后。因此，为了有效地抑制周期性轨迹震荡，选取飞行器高度变化率首次为0 的状态作为初始下降段与滑翔段的交班时刻，即

进入滑翔段之后，在每个制导周期内，给定初始倾侧角σini的幅值，从当前状态对运动方程进行积分(倾侧角符号由侧向制导逻辑决定)，则能够得到滑翔飞行末端时刻的待飞航程偏差:

式中待飞航程s 选取星下点圆弧长度进行近似计算:

则使待飞航程误差f 为0 的倾侧角幅值可通过割线法快速求解，具体计算公式［6］为

结合(13)式～(15)式能求得当前制导周期内倾侧角指令σcmd的幅值(符号由侧向制导逻辑决定)。在不依赖于QEGC 约束的情况下，该制导指令无法导引飞行器完成平稳再入飞行。为此，本文在文献［21］的基础上，设计了一种简易可行的倾侧角反馈控制律以抑制再入滑翔轨迹的周期性震荡，具体计算公式为

纵向制导律的设计思想是在倾侧角外环控制回路添加高度变化率反馈，以抑制再入滑翔过程中产生的高度轨迹震荡。通常，高超声速飞行器再入大气层后会在首次拉起过程中产生最明显的轨迹震荡，之后，震荡幅值随着速度的下降而逐渐衰弱。因此，在滑翔飞行前期，倾侧角反馈控制律(16)式应侧重于抑制再入轨迹震荡，选取较大的增益;在滑翔飞行后期，反馈控制律(16)式应侧重于待飞航程的校正，选取较小的增益，故采用分段递减函数表示增益系数:

式中:k1和k2根据实际再入初始状态及终端约束来设定。本文中，k1取20 ～30，k2取10 ～15. 通过Monte-Carlo 仿真实验及分析可以证明，分段选取增益参数k 的方法具有可行性。

图1 参考高度变化率示意图Fig.1 Example of reference altitude rate

2.2 侧向制导律设计

侧向制导律的主要任务是确定倾侧角控制指令的符号。为了实现再入滑翔飞行的侧向轨迹控制，必须寻找合适的倾侧角反转逻辑。传统的侧向制导律往往简单设计了横程误差走廊(或航向角误差走廊)来实现倾侧角的反转控制。实际上，同时考虑横程误差和航向角误差对倾侧角指令符号的影响，才能更为合理和准确地实现飞行器的侧向运动控制。因此，本文引入归一化误差:

式中:Δχ 为横程误差;p 为权值系数，0≤p≤1. p 的大小决定了归一化误差δ 侧重于体现航向角误差还是横程误差。通常情况下p 取0.4 ～0.6 即能满足侧向制导要求。

以归一化误差δ 为基础设计侧向误差走廊可以兼顾横程误差和航向角误差对倾侧角反转指令的影响，其形式如图2所示。

图2 侧向误差走廊设计Fig.2 Design of lateral error corridor

侧向制导逻辑为:当归一化误差δ 超出误差走廊的上边界时，倾侧角指令符号为负;当归一化误差δ 超出走廊的下边界时，倾侧角指令为正;当归一化误差δ 位于误差走廊内时，倾侧角符号保持不变。该制导逻辑的具体计算公式为

3 仿真分析

本文以升力式高超声速再入飞行器CAV-H 为仿真对象，其主要特征参数为:飞行器质量m =907.2 kg，气动参考面积Sref=0.483 9 m2，最大热流密度约束Qmax=1.0 MW/m2，最大动压约束qmax=80 kPa，最大过载约束nmax=4.0 g.

飞行器初始再入状态如表1所示。终端状态约束为:终端目标位置(E90°，N30°)，终端高度20 km，终端速度1 800 m/s. 标称攻角剖面参数:K=0.11，α0=22°，VT的Ma=16. 倾侧角指令的取值范围为-85° ～85°. 倾侧角反馈控制律参数k1= 25，k2=10.归一化误差系数p =0.5. 仿真计算机操作系统为Windows XP，主频3.0 GHz，内存2.0 GB. 制导程序采用标准C/C + + 语言编写，制导周期为1 s.

表1 飞行器初始再入状态Tab.1 Initial reentry conditions of vehicle

3.1 标准条件下制导方法仿真分析

为了验证本文提出制导算法的优越性和可靠性，设计以下两个算例:算例1 采用传统的预测校正再入制导方法;算例2 采用本文改进的预测校正制导算法。图3(a)～图3(h)给出了标准条件下(不 考虑再入点散布误差)的制导算法仿真结果。

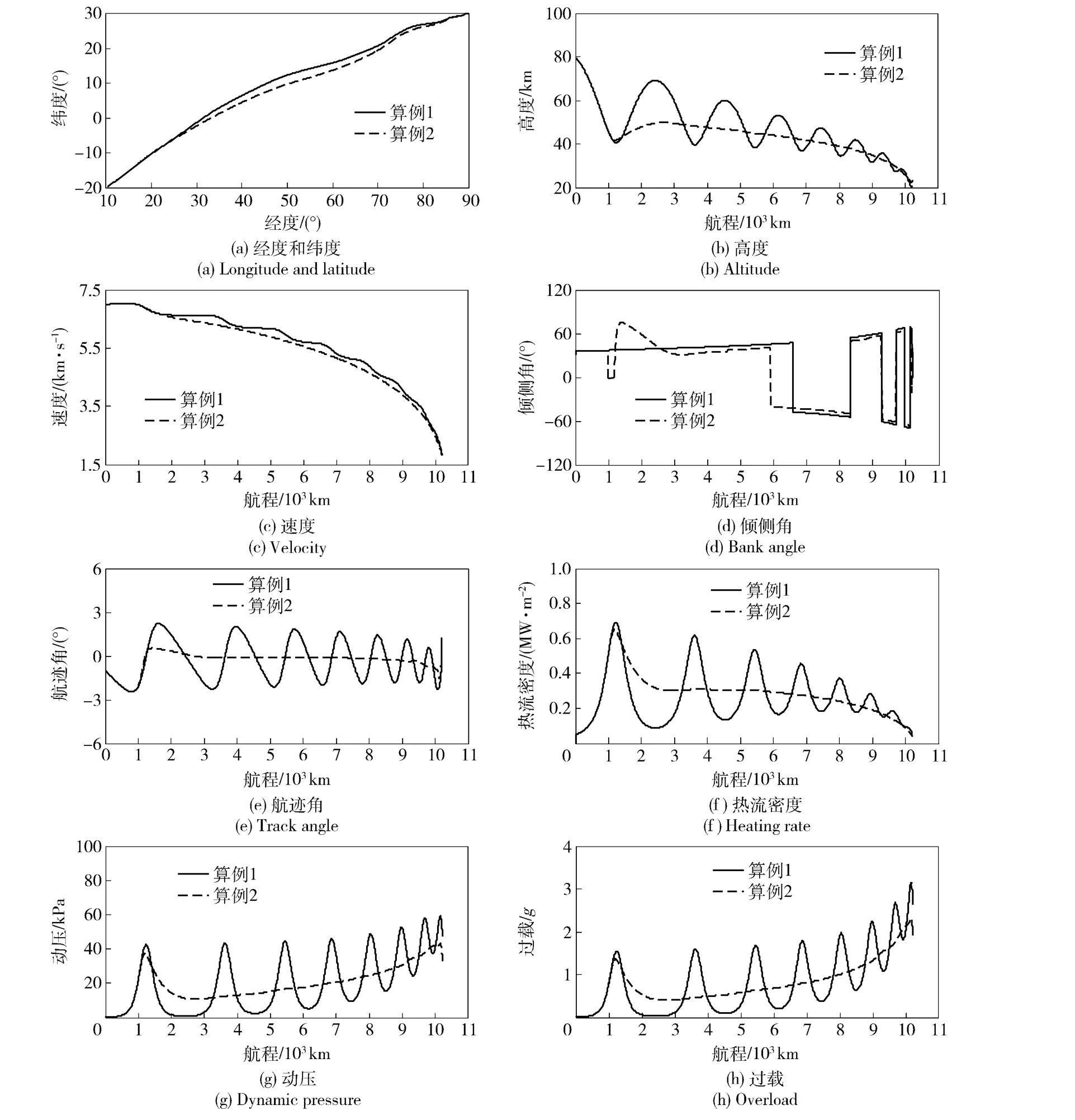
图3 标准条件下制导仿真结果Fig.3 Simulation results of reentry guidance in standard conditions

通过对比可得出以下结论:

1)算例1 的落点经度、纬度分别为90.02°和30.02°，精度误差为3.15 km，算例2 的落点经度、纬度分别为89.98°和30.05°，精度误差为5.91 km，两种算法的经度、纬度误差均小于0.1°，落点距目标距离不超过10 km，满足了制导方法的精度要求。

2)仿真算例主要针对再入滑翔段制导，即高度80 km 降至20 km，不包括高度20 km 降至地面0 km的末制导问题。因此，与给定终端飞行高度20 km和终端速度1 800 m/s 相比，两种算法仿真结果的落点高度误差小于1.5 km，落点速度误差小于30 m/s.且与算例1 相比，算例2 飞行高度轨迹未出现周期性震荡，飞行速度曲线较为平滑，验证了本文提出的倾侧角反馈控制律具有可行性。

3)热流密度、动压和过载约束均未超过给定的最大值限度，与算例1 相比，算例2 中上述典型硬约束的曲线更加平滑且无周期性震荡，热/压防护效果良好。

4)与算例1 相比，算例2 中倾侧角反馈控制律仅在幅值上做出了修正，没有增加制导指令反转的次数，体现了制导算法的可靠性。

5)值得注意的是，算例1 和算例2 的仿真结果主要用于说明本文提出的倾侧角反馈控制律能够有效地抑制轨迹震荡，因而算例1 选取了未添加QEGC 的预测校正制导算法进行对比。从理论上讲，添加QEGC 与倾侧角反馈控制率都可以有效地抑制再入轨迹震荡，但传统的QEGC 仅仅能够限制高度震荡的上边界，且在航迹角增大或轨道再入速度较低等特殊情况下有可能失效，可见本文提出的算法更具有普遍适用性。

3.2 扰动条件下制导方法仿真分析

再入滑翔飞行过程中，大气模型参数的不确定性和动力学系统的强扰动性都可能造成高超声速飞行器偏离预定轨迹和目标，从而导致任务失败。为了验证本文提出的制导算法在各种参数偏差条件下都具有鲁棒性，针对不同初始扰动情况下的再入滑翔制导进行了Monte Carlo 仿真实验。再入点初始散布偏差项、分布类型及偏差限度见表2.

表2 再入点散布误差Tab.2 Dispersions at the reentry interface

图4(a)～图4(i)给出了扰动条件下制导算法的仿真曲线和落点散布情况统计。通过分析可得出以下结论:

1)如图4(a)所示，从星下点轨迹可看出，在误差和扰动存在的情况下，仿真飞行过程没有偏离原始的再入滑翔轨迹，整体上能满足预定的飞行航程要求。

2)如图4(b)所示，在Monte Carlo 数值仿真算例中，高度曲线未出现周期性的振荡现象，再入飞行轨迹比较平稳，且终端高度和速度约束能够满足制导要求，热流、动压和过载也未超过给定的最大约束限制，如图4(f)～图4(h)所示，验证了本文提出算法的鲁棒性。

3)根据落点散布误差可得，如图4(i)所示，再入落点距给定终端目标的距离不超过15 km，且经度、纬度误差均小于0.15°，满足了预测校正制导的精度要求。

4)从倾侧角曲线的变化趋势可知，在再入滑翔飞行的前半段，控制指令主要受到高度反馈变化率的影响，而归一化误差走廊更多地作用于再入滑翔飞行的后半段。

5)对比不同扰动条件对预测校正制导的影响程度能够发现，速度偏差和航迹角偏差对制导精度的影响相对较大，而高度偏差对制导精度的影响相对较小。

4 结论

本文针对大升阻比高超声速飞行器再入制导问题，提出一种改进的倾侧角反馈控制律和侧向误差走廊，研究分析和仿真结果表明:

1)考虑轨迹震荡抑制的倾侧角反馈控制、不改变传统预测校正制导律的表达形式和倾侧角反转的次数，易于实现。

2)归一化的侧向误差走廊设计同时兼顾了横程误差和航向角误差对倾侧角反转逻辑的影响，使侧向运动控制更加合理和有效。

3)标准条件下的仿真结果表明，与传统的预测校正制导相比，本文提出的制导方法能够有效地抑制再入轨迹的周期性震荡。

4)扰动条件下的Monte Carlo 仿真结果表明，本文提出的制导方法具有良好的鲁棒性。

图4 扰动条件下制导仿真结果Fig.4 Simulation results of reentry guidance with random disturbance

References)

［1］Sarah N D，Nesrin S K. Survey of planetary entry guidance algorithms［J］. Progress in Aerospace Sciences，2014，68(1):22 -28.

［2］Zhao J，Zhou R. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints［J］. Chinese Journal of Aeronautics，2013，26(6):1544 -1553.

［3］袁宴波，张科，薛晓东. 基于Radau 伪谱法的制导炸弹最优滑翔弹道研究［J］. 兵工学报，2014，35(8):1179 -1186.YUAN Yan-bo，ZHANG Ke，XUE Xiao-dong. Optimization of glide trajectory of guided bombs using a Radau pseudo-spectral method［J］.Acta Armamentarii，2014，35(8):1179 -1186. (in Chinese)

［4］Zhao J，Zhou R，Jin X. Progress in reentry trajectory planning for hypersonic vehicle［J］. Journal of Systems Engineering and Electronics，2014，25(4):627 -639.

［5］赵江，周锐. 考虑禁飞区规避的预测校正再入制导方法［J］.北京航空航天大学学报，2015，41(5):864 -870.ZHAO Jiang，ZHOU Rui. Predictor-corrector reentry guidance with no-fly zone constraints［J］. Journal of Beijing University of Aeronautics and Astronautics，2015，41(5):864 -870. (in Chinese)

［6］Xue S，Lu P. Constrained predictor-corrector entry guidance［J］.Journal of Guidance Control and Dynamics，2010，33(4):1273 -1281.

［7］王智，唐硕，闫晓东. 高超声速滑翔飞行器约束预测校正再入制导［J］. 飞行力学，2012，30(2):175 -180.WANG Zhi，TANG Shuo，YAN Xiao-dong. Constrained predictorcorrector reentry guidance for hypersonic glide vehicle［J］. Flight Dynamics，2012，30(2):175 -180. (in Chinese)

［8］刘冠南，周浩，陈万春. 高超声速飞行器再入多段导引方法研究［J］. 飞行力学，2012，30(4):337 -341.LIU Guan-nan，ZHOU Hao，CHEN Wan-chun. A study on the multiple phrase reentry guidance method of hypersonic vehicle［J］.Flight Dynamics，2012，30(4):337 -341. (in Chinese)

［9］王青，冉茂鹏，赵洋. 基于预测校正法的高超声速飞行器再入制导［J］. 北京航空航天大学学报，2013，39(12):1564 -1568.WANG Qing，RAN Mao-peng，ZHAO Yang. Reentry guidance for hypersonic vehicle based on predictor-corrector method［J］. Journal of Beijing University of Aeronautics and Astronautics，2013，39(12):1564 -1568. (in Chinese)

［10］王青，莫华东，吴振东，等. 基于能量的高超声速飞行器再入混合制导方法［J］. 北京航空航天大学学报，2014，40(5):580 -585.WANG Qing，MO Hua-dong，WU Zheng-dong，et al. Energybased hybrid reentry guidance for hypersonic vehicles［J］. Journal of Beijing University of Aeronautics and Astronautics，2014，40(5):580 -585. (in Chinese)

［11］曾宪法，王洁瑶，王小虎. 基于能量和解析预测校正的滑翔制导［J］. 系统工程与电子技术，2013，35(12):2583 -2589.ZENG Xian-fa，WANG Jie-yao，WANG Xiao-hu. Gliding guidance based on energy and analytical predictor-corrector［J］. Systems Engineering and Electronics，2013，35(12):2583 -2589.(in Chinese)

［12］李强，夏群利，何镜，等. 基于大气预估的再入飞行机动减速制导方法［J］. 兵工学报，2013，34(9):1091 -1096.LI Qiang，XIA Qun-li，HE Jing，et al. Maneuvering-deceleration guidance algorithm based on atmosphere estimation for reentry vehicle［J］. Acta Armamentarii，2013，34(9):1091 -1096. (in Chinese)

［13］梁子璇，任章. 基于在线气动参数修正的预测制导方法［J］.北京航空航天大学学报，2013，39(7):853 -857.LIANG Zi-xuan，REN Zhang. Predictive reentry guidance with aerodynamic parameter online correction［J］. Journal of Beijing University of Aeronautics and Astronautics，2013，39(7):853 -857. (in Chinese)

［14］Wang J，Qu X，Ren Z. Hybrid reentry guidance based on the online trajectory planning［J］. Journal of Astronautics，2012，33(9):1217 -1224.

［15］王俊波，田源，任章. 基于最优化问题的混合再入制导方法［J］.北京航空航天大学学报，2010，36(6):736 -740.WANG Jun-bo，TIAN Yuan，REN Zhang. Mixed guidance method for reentry vehicles based on optimization［J］. Journal of Beijing University of Aeronautics and Astronautics，2010，36(6):736 -740. (in Chinese)

［16］Shen Z，Lu P. Onboard generation of three dimensional constrained entry trajectories［J］. Journal of Guidance，Control，and Dynamics，2003，26(1):111 -121.

［17］Leavitt J A，Mease K D. Feasible trajectory generation for atmospheric entry guidance［J］. Journal of Guidance，Control，and Dynamics，2007，30(2):473 -481.

［18］Zhao J，Zhou R，Jin X. Reentry trajectory optimization based on a multistage pseudospectral method［J］. Scientific World Journal，2014(878193):1 -13.

［19］Zhao J，Zhou R，Jin X. Gauss pseudospectral method applied to multi-objective spacecraft trajectory optimization［J］. Journal of Computational and Theoretical Nanoscience，2014，11 (10):2242 -2246.

［20］Lu P，Xue S. Rapid generation of accurate entry landing footprints［J］. Journal of Guidance Control and Dynamics，2010，33(3):756 -767.

［21］Lu P. Entry guidance:a unified method［J］. Journal of Guidance，Control，and Dynamics，2014，37(3):713 -728.