基于粒子群的Vague均值聚类分割算法

田小平， 史鹏敏， 吴成茂

(西安邮电大学 电子工程学院，陕西 西安 710121)

基于粒子群的Vague均值聚类分割算法

田小平， 史鹏敏， 吴成茂

(西安邮电大学 电子工程学院，陕西 西安 710121)

将Vague 集引入模糊C-均值聚类目标函数，对其添加非隶属度信息，定义样本关于类的肯定隶属度函数和否定隶属度函数，并构造聚类中心表达式。采用粒子群优化算法求解该聚类目标函数，设计相应聚类算法，使其快速收敛于目标函数的全局最优解。对比实验结果表明，改进算法可以分割出目标轮廓并具有抗噪性。

聚类算法；粒子群优化算法；Vague 集；粒子

图像分割[1-2]是基于某种相似准则对像素进行分类，使得同类像素不仅在数值上相似，而且在空间位置上也具有紧密的联系。由于图像分割的本质是像素分类问题，于是会存在许多模糊性的不确定信息和数据。针对这些模糊信息，Fuzzy集理论[3]被提出并应用在图像分割方面[4-5]。其主要特征是在论域U中每个元素ui被赋予一个[0,1]的数作为隶属度，其隶属度是一个单值。单值隶属度既包含了支持ui的证据，也包含了反对ui的证据，但它无法同时表示支持和反对的证据。文献[6]引入Vague集理论，在一个Vague集中，用一个真隶属度函数tA和一个假隶属度函数fA来描述隶属度的界，构成了隶属度区间[tA(ui),1-fA(ui)],其中0≤tA(ui)+fA(ui)≤1。Vague集最大的特点和优点是它能同时表示支持和反对的证据[7]。

聚类分析[8-10]是一种将研究对象分为相对同质的群组的统计分析技术，而模糊聚类是聚类分析领域中的重要组成部分。在模糊聚类算法中，模糊C-均值聚类算法(Fuzzy C-means Clustering, FCM)[11]是一种非监督模糊聚类算法， 对于图像目标和背景所占比例相差不悬殊时能获得较好的分割效果，但对初始化敏感而且容易陷入局部极小值[12]。而一种基于粒子群模糊C-均值聚类算法[13-15](Particle swarm-based Fuzzy clustering Algorithms, PFA)在图像分割方面，具有一定的抗噪性，且比FCM算法分割效果好。但是，当图像较为复杂时，该算法就不能有效的进行分割。因此，本文构造一种基于粒子群的Vague均值聚类算法(Particle swarm-based Vague clustering Algori-thms, PVA)。该算法是将粒子群优化(Particle swarm optimization, PSO)算法[16-18]和基于Vague集聚类算法(Vague C-means Clustering,VCM)相结合，将图像中的目标从背景中分割出来，并与FCM算法以及PFA算法进行比较。

1 粒子群优化算法

PSO算法是将每一个优化问题的解视为搜索空间中的一只鸟，称之为一个微粒。所有的微粒都通过被优化的适应度值来衡量微粒的优劣，其中每个微粒在n维搜索空间中以一定的速度决定它们飞行的方向和距离。然后，微粒根据自身的飞行情况以及其他微粒的飞行情况，来动态地调节整体的飞行速度，以便向群体中最好微粒位置靠近，从而在解空间中搜素到最优解。

PSO算法的数学描述：假设在一个d维搜索空间中，种群中的粒子数目为M，由M个粒子组成的群体X={x1,x2,…,xM},i的取值范围为[1,M],第i个粒子在t时刻的位置为

xi(t)=[xi1(t),xi2(t),…,xid(t)]，

粒子的速度为

vi(t)=[vi1(t),vi2(t),…,vid(t)]。

速度和位置表达式[16]分别为

vid(t+1)=w×vid(t)+c1×r1×(pid(t)-

xid(t))+c2×r2×(pgd(t)-xid(t)),

(1)

xid(t+1)=xid(t)+vid(t+1)。

(2)

其中：c1和c2为两个非负常数；r1和r2是[0,1]区间上均匀分布的随机数；w为惯性权值，w的取值范围为[0,1.4][17]；pid表示第i个粒子在d维空间中所经历过的最好位置；pgd表示全局最好位置。

PSO算法利用式(1)和式(2)对粒子的速度和位置反复进行更新，直到满足迭代终止条件或者到达最大迭代次数。

2 聚类算法

2.1 模糊C-均值聚类算法

模糊C-均值聚类所对应的目标函数[1]为

(3)

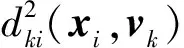
(4)

为使目标函数达到最小值，采用拉格朗日乘子λi，使得目标函数关于隶属度uki和聚类中心vk的偏导数为零，求得

(5)

(6)

模糊C-均值聚类算法对图像进行分割具有直观和易于理解及实现的特点[19]。但是，当图像中存在异常值时，该算法不能有效地识别噪声，产生的聚类结果与实际情况并不一致，很难获得满意的分割效果。

为了改善模糊C-均值聚类算法的分割性能，将粒子群引入模糊C-均值聚类得到一种基于PSO的模糊聚类(PFA)算法。设一个由M个粒子组成的群体为X={x1,x2,…,xM}，其适应度函数[14]为

(7)

在粒子群中每一个粒子通过不同维的取值所产生多个聚类结果，直到搜索到最优位置使适应函数达到终止条件或达到最大迭代次数。PFA算法与FCM算法最大的区别在于不再使用C均值方法而使用PSO算法来确定聚类中心[14]。

2.2 Vague聚类算法

Vague集能够更好地表示区间模糊信息和多维度模糊信息，于是将Vague 集引入传统模糊C-均值聚类目标函数，对其进行适当修改并获得一种改进的Vague集聚类目标函数。

2.2.1 Vague集

设U={u1,u2,…,un}为论域，其中i∈{1,2,…,n}，任意元素ui都属于U。U中的一个Vague集A用一个真隶属度函数tA和一个假隶属度函数fA来表示，tA(ui)是从支持ui的证据中推导出的肯定隶属度的下界，fA(ui)是从反对ui的证据中推导出的否定隶属度的下界，以上两个下界在区间[0,1]上构成了一个子区间[tA(ui),1-fA(ui)]，其中0≤tA(ui)+fA(ui)≤1。因此，论域U中的一个Vague集A的表达式[7]为

其中0≤tA≤1-fA≤1且1≤i≤n。

在Vague集A中的元素ui的隶属度是区间[0,1]的子区间即[tA(ui),1-fA(ui)]，亦即，或许无法知道ui的精确隶属度μA(ui)，但是μA(ui)一定界于tA(ui)和1-fA(ui)之间。

函数πA=1-tA(ui)-fA(ui)称之为A中元素ui的未知度[20]。其中πA的取值范围为[0,1],利用πA对μA(ui)的认识精度进行衡量，未知度越大，认识精度越低。

2.2.2 基于Vague均值聚类算法

设一幅图像由n个像素组成，每一个像素的灰度值为xi，这幅图像被分成c个类。Vague集聚类算法(VCM)的目标函数表达式[21]如下

(8)

其中c是样本分类的个数，n为样本个数，vj(j=1,2,…,c)是聚类中心。h(i)表示每个灰度值出现的次数。tij表示像素i属于第vj个聚类中心的真隶属度。fij表示像素i属于第vj个聚类中心的假隶属度。真的隶属度tij和假的隶属度fij的表达式分别为

(9)

(10)

其中d2(xi,vj)为欧氏距离即d(xi,vj)=‖xi-vj‖。λ是正的常数，通常取λ=2。真的隶属度tij和假的隶属度fij之间的关系为0≤tij+fij≤1。则推导过程如下。

情况1设聚类个数c=2

可得ti1+fi1=1，同理ti2+fi2=1。此时，未知度πij=1-tij-fij=0。

情况2设聚类个数c1>2(∀c1,c2>2且c1-c2=1)。

由c1-c2=1可得

同理

由以上式子可得

综合情况1和情况2，可得0≤ti1+fi1≤1。当聚类个数c增大时，tij+fij的值减小，从而使未知度πij的值增大。

在FCM算法中，采用最大隶属度原则将样本数据划分为不同的类，但当样本数据属于多个类的隶属度几乎相等时，就无法具体判断该数据到底属于哪一类。此时，采用最大隶属度原则会出现错误的分类结果。然而，在VCM算法中，采用uij=tij来描述样本数据xi对第j类的隶属度，即克服了模糊C-均值聚类算法的不足。

3 基于粒子群的Vague聚类算法

3.1 PVA算法的思想

为了使Vague集聚类目标函数快速收敛于全局最优解，构造PVA算法。假设X={x1,x2,…,xM}是由M个d维粒子组成的群体。用粒子群中任意一个微粒xi代替一个聚类中心集合vi。则微粒的适应度函数可表示为

(11)

其中：m为模糊因子，一般情况下m=2；β为权重系数；tij+fij的取值范围为[0,1]之间。

在粒子群中每一个粒子通过不同维的取值会产生多个聚类结果，直到搜索到最优位置使适应度函数达到终止条件或到达最大迭代次数。

3.2 PVA算法的设计

利用式(1)和式(2)进行迭代，PVA算法的步骤如下。

步骤1设置c1和c2为非负常数，群体规模M和最大迭代次数T,并对粒子群的随机位置和速度进行初始化。

步骤2通过式(9)和式(10)计算真隶属度tij和假的隶属度fij。

步骤3计算每个粒子的适应值。

步骤4对于每个粒子xi，将其适应值与迄今为止所经历的最好位置pi的适应值进行比较，若优于pi的适应值，则将其作为当前最好位置。

步骤5对于每个粒子xi，将其适应值与全局所经历的最好位置pg的适应值进行比较，若优于pg的适应值，则将其作为全局最好位置。

步骤6根据式(1)和式(2)对粒子的速度和位置进行更新。

步骤7若取得最优位置满足预定最小适应阈值或达到最大循环次数，迭代终止，否则，返回步骤3。

步骤8所获得pgd的粒子，通过式(9)和式(10)可以得到更新后真的隶属度tij和假的隶属度fij。

4 实验结果与分析

分别采用FCM算法、PVA算法和PFA算法对巴黎河流遥感图像、海豚图像、大脑CT图像和老鹰图像(图1)进行图像分割测试,分割结果分别如图2～图5所示。

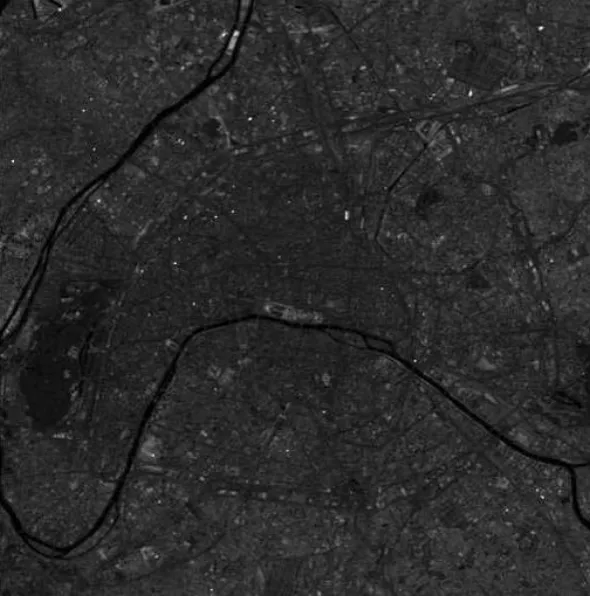
(a) 巴黎河流遥感图像

(b) 海豚图像

(c) 老鹰图像

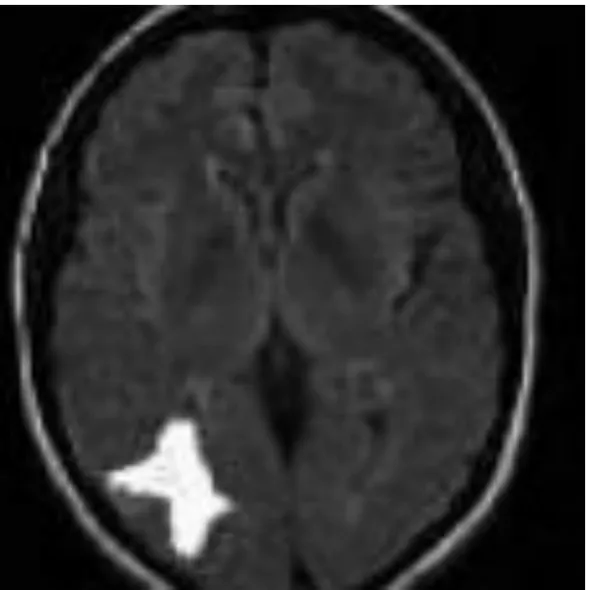
(d) 大脑CT图像

(a) FCM 算法

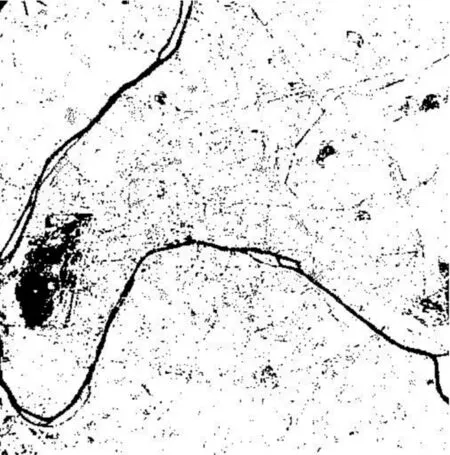
(b) PFA算法

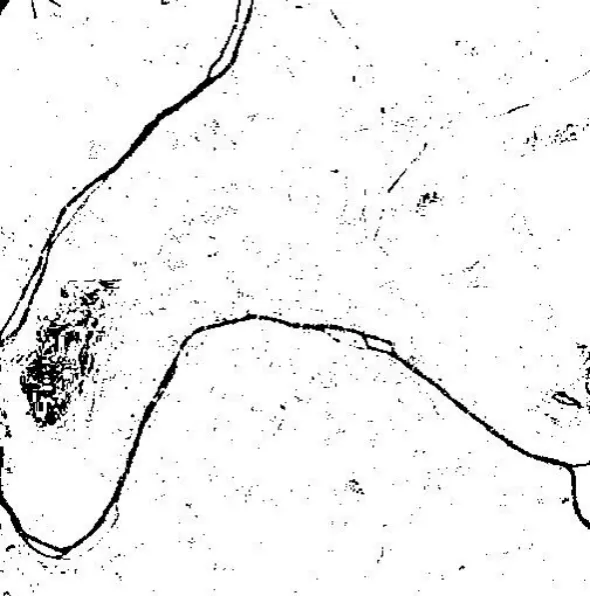
(c) PVA算法

从图2所示的3种分割结果来看，图2(a)噪声很大，目标不能从背景中有效地分割出来，图2(b)和图2(c)都能清晰地分割出目标，但采用PVA算法分割的效果最好，噪声较小且目标轮廓清晰连续。

(a) FCM 算法

(b) PFA算法

(c) PVA算法

从图3所示的分割结果来看，3种分割结果并非完全相同，其中图3(a)的分割结果明显比图3(b)和图3(c)的分割结果差，图3(a)中的目标和背景完全混淆。相比图3(b)来说图3(c)更能体现出目标的清晰度以及伴随噪声小的特点。

(a) FCM 算法

(b) PFA算法

(c) PVA算法

从图4所示的分割结果来看，3种算法都能有效地将目标从背景中分割出来，但是图4(a)和图4(b)的背景噪声明显大于图4(c)中的噪声，表明采用PVA算法的分割效果更好，具有较好的抗噪能力。

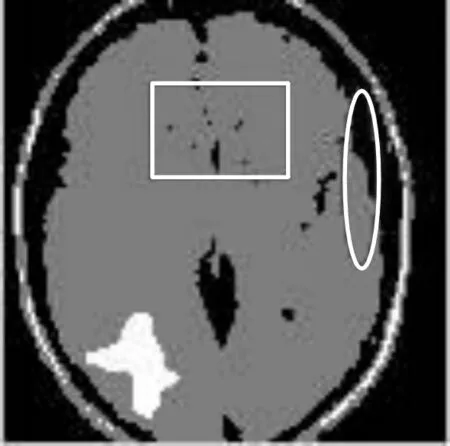
(a) FCM 算法

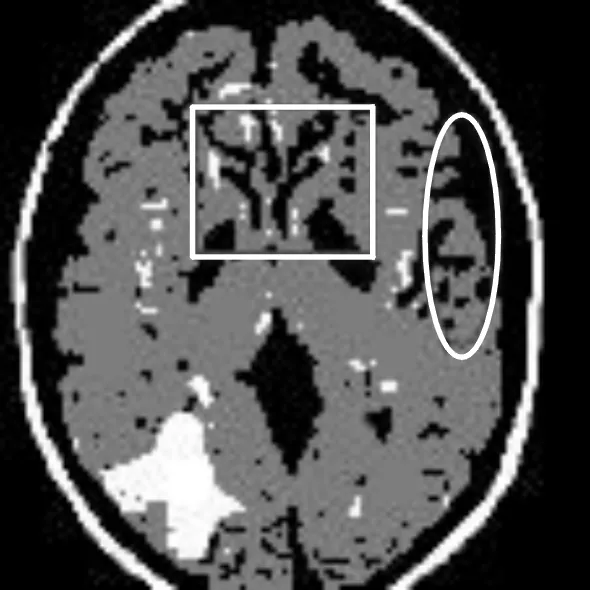
(b) PFA算法

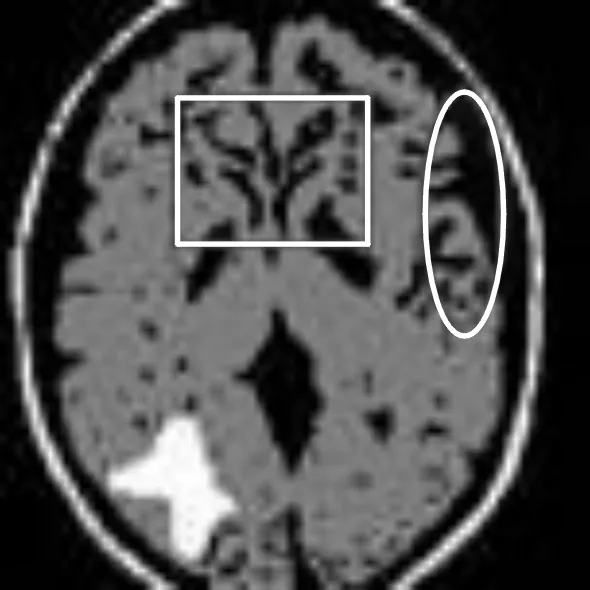
(c) PVA算法

从图5所示的分割结果可以看出，图5(a)中的长方形区域以及椭圆区域的轮廓分割效果差，但是图5(b)和图5(c)中的长方形区域以及椭圆区域却保留了其轮廓的完整性。对比图5(b)和图5(c)中的长方形区域可以看出，图5(c)中的长方形区域内所含噪声小于图5(b)中长方形区域所含的噪声。

通过巴黎河流遥感图像、海豚图像、大脑CT图像以及老鹰图像的测试结果来看，PVA分割算法是正确且合理的，相比FCM算法、PFA算法具有更好的抗噪性和优化能力。

5 结束语

结合粒子群优化算法(PSO)和Vague均值聚类算法(VCM),得到一种基于PSO的Vague均值聚类分割(PVA)快速算法。PSO的引入提高了该聚类目标函数到达全局最优解的收敛速度。采用FCM、 PFA和PVA算法对人工合成图像和遥感图进行分割比较，实验结果表明 PVA算法对图像轮廓分割方面比较细致且具有一定的抗噪性，其效果明显优于其他算法的分割效果。

[1] 李旭超,刘海宽,王飞,等.图像分割中的模糊聚类方法[J].中国图像图形学报,2012,17(4):447-458.

[2] Li Chunming, Xu Chenyang, Gui Changfeng, et al. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3243-3254.

[3] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353.

[4] Hu Dan,Lin Tsau young,Fan Qiang. The construction of general Type-2 Fuzzy Sets[C]//IEEE International conference on Granular Computing. Beijing: IEEE, 2013:141-146.

[5] Wang Wei,Peng Jinye,Chen Penggang. A new method of transforming fuzzy set into vague set and its application[C]//IEEE International Conference on Consumer Electronics, Communications and Networks. Yichang:IEEE,2012: 808-811.

[6] Gau W L, Buehrer D J. Vague sets[J]. IEEE Trans on Systems Man Cybernetics,1993,23(2):610-614.

[7] 张文彬,余建坤.基于Vague集的模糊聚类算法研究[J].云南民族大学学报，2008,17(1):18-23.

[8] 唐东明.聚类分析及其应用研究[D].成都:电子科技大学，2010:13-20.

[9] Kanungo T, Mount D M, Netanyahu N S, et al. An efficient k-means clustering algorithm: Analysis and implementation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2002, 24(7):881-892.

[10]de Oliveira J V, Pedrycz W.(Eds.). Advances in fu-zzy clustering and its applications[M].New York: Wiley,2007:333-367.

[11]支晓斌,田溪.判别模糊C-均值聚类算法[J].西安邮电大学学报,2013,18(5):26-30.

[12]李琳,范九伦,赵凤.模糊C-均值聚类图像分割算法的一种改进[J].西安邮电大学学报,2014,19(5):56-60.

[13]Biswal B, Dash P K, Panigrahi K B. Power quality disturbance classification using fuzzy C-means al-gorithm and adaptive particle swarm optimization[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (1): 212-220.

[14]冯征,阎敏,张智峰.一种基于PSO的模糊聚类算法[J].计算机工程与应用，2006,42(27):150-165.

[15]Juang C F, Hsiao C M, Hsu C H. Hierarchical cluster-based multispecies particle-swarm optimization for fuzzy-system optimization[J].IEEE Transactions on Fuzzy Systems,2010,18(1): 14-26.

[16]Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]// IEEE International Conference on Systems,Man, and Cybernetics, Compu-tational Cybemetics and Simulation .Orlando,FL: IEEE ,1997,5:4104-4108.

[17]Sun Qi, Zhang Fuyu. Particle Swarm Optimization[J]. Computer Knowledge & Technology, 2007, 1(6):9-40.

[18]Banks A, Vincent J, Anyakoha C. A review of particle swarm optimization. Part I: background and develop-ment[J]. Natural Computing, 2007, 6(4): 467-484.

[19]李岩波,韩啸.基于空间模糊聚类的图像分割优化算法[J].吉林大学学报,2014,52(3):565-567.

[20]王伟.基于Vague集理论的推荐与模糊决策相关算法研究[D].西安:西北大学,2014:11-21.

[21]Xu Chao, Zhang Peilin, Li Bing,et al.Vague C-means clustering algorithm[J].Pattern Recognition Letters, 2013,34(5): 505-510.

[责任编辑：祝剑]

Vague means clustering segmentation algorithm based on particle swarm

TIAN Xiaoping, SHI Pengmin, WU Chengmao

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121,China)

Introduce the Vague set and add its non-membership information into the objective function of fuzzy C-means clustering algorithm, to get a modified objective function of Vague clustering. After the acceptance function and denial function of every sample with regard to a class are defined, and an expression of the sample center is set up, try to solve this objective function with particle swarm optimization algorithm, and design a modified corresponding clustering algorithm, to ensure that, the objective function converges fast to a global optimum solution. A comparative experiment is offered to show that, the modified algorithm can segment the outline of the target more clearly, and it is of good noise-immunity.

clustering algorithm, particle swarm optimization algorithm, Vague set, particle

2014-12-26

国家自然科学基金重点资助项目(61136002);陕西省自然科学基金资助项目(2014JM8331, 2014JQ5138,2014JM8307)

田小平 (1963-)，男，教授，从事信号与信息处理技术研究。E-mail:xptian@xupt.edu.cn 史鹏敏 (1989-)，女，硕士研究生，研究方向为图像处理及其信息安全。E-mail:1023968083@qq.com

10.13682/j.issn.2095-6533.2015.06.013

TP391.4

A

2095-6533(2015)06-0061-05