储层条件下页岩样品吸附潜力预测模型

李 新,冀 昆,方朝强,刘 鹏,李 兵

(1.西北大学 地质学系, 陕西 西安 710069;2.中国石油集团测井有限公司 技术中心,陕西 西安 710077;3.中国石油天然气集团公司 测井重点实验室,陕西 西安 710077)



·地球科学·

储层条件下页岩样品吸附潜力预测模型

李 新1,2,3,冀 昆2,3,方朝强2,3,刘 鹏2,3,李 兵2,3

(1.西北大学 地质学系, 陕西 西安 710069;2.中国石油集团测井有限公司 技术中心,陕西 西安 710077;3.中国石油天然气集团公司 测井重点实验室,陕西 西安 710077)

合理预测页岩在储层温度和压力条件下的吸附量对于储层描述、资源量的估算具有重要意义,而等温吸附试验下的温度与储层真实温度出入较大。该研究以吸附势理论为基础，构建吸附量随温度压力变化的模型,通过样品在30℃的吸附数据建立的关系模型,理论上可以预测样品在任意温度压力条件下的吸附量。对比60℃和90℃时等温吸附实际数据与该模型预测的吸附量发现:低温下，模型预测的吸附量与实验值较为符合，但压力增高的情况下,模型的精度也随之降低；运用球状模型对最大吸附量进行限定，能较好地纠正高压下的偏差。

页岩气;吸附气;吸附势理论;吸附特性曲线;饱和吸附量

在页岩储层中,甲烷主要以游离态和吸附态存在,页岩的吸附能力介于煤层(吸附气量大于85%)和常规圈闭气(吸附气通常为0)之间[1]。吸附态甲烷是页岩气一种重要的储存形式，同时，页岩吸附数据是页岩气资源评价、产能预测的重要参数。影响页岩吸附量的因素分为内因和外因,内因即是页岩的有机质含量、有机质成熟度以及矿物成分;外因即是所在储层的温度压力条件,这些条件综合决定了页岩的吸附潜力。获得页岩样品的吸附数据常用的方式是等温吸附实验,现有等温吸附实验温度大都在30℃,而国内的页岩气藏普遍埋藏较深(见图1),因此，实验中的温度往往低于页岩储层的实际温度。不仅如此,随着埋深增加,储层温度和压力是一个动态变化的过程,等温吸附实验在固定的温度下测得的吸附数据难以反应储层的真实吸附量。前人在温度、压力同时变化时，固体对气体吸附量的变化规律上有过研究,Kim等人通过把温度作为吸附的变量之一[2],提出了计算煤吸附气体的经验公式;钟玲文等[3]用多个温度下的等温吸附实验,发现在不同压力下,温度和吸附量呈线性关系;赵志根等[4]也利用不同温度下的等温吸附实验,建立了饱和吸附量和温度之间的关系;胡涛[5]在研究固-气吸附体系的时候,提出用吸附热来预测其他温度下的吸附量,但该算法至少需要两个温度点的吸附数据。

吸附势理论已经在煤层气领域有较多的发展和应用,页岩气和煤层气有许多相似之处,本文将验证页岩气也符合吸附势理论的相关假设前提,并用吸附势理论建立起吸附量与温度压力的关系模型。

图1 西北区不同埋深页岩气P50资源量分布Fig.1 P50 shale gas resources distribution at different depth in Northwest

1 等温吸附实验

本次研究的页岩岩心样品采自石柱地区侏罗系,该地区以滨浅湖—半深湖沉积为主,样品的基本数据见表1。等温吸附采用300型等温吸附仪,样品分别在30℃，60℃，90℃下进行高压等温吸附实验。等温吸附方法和标准采用GB/T 19560-2004标准执行,等温吸附实验结果见图2。由图2可见，当温度一定时,该样品的吸附量和压力的关系符合Langmuir公式：在同一温度下,压力越高,吸附量越大；在压力一定的情况下,随着温度增高,吸附量有减小的趋势。在低压时吸附量增加迅速,随着压力的增加,吸附量增加的速度逐渐减小趋于0。

表1 样品基本资料Tab.1 Basic information of samples

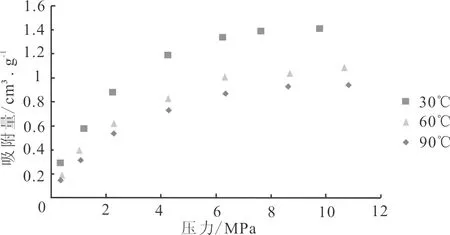
图2 样品在不同温度下的等温吸附数据Fig.2 Isotherm data at different tempreture

2 建立吸附特性曲线

Polanyi在1914年提出吸附势理论,该理论认为固体表面就像行星的重力场一样,对附近的吸附质分子有一个引力,吸附质分子被吸引到表面,形成多分子吸附层[6]。甲烷在页岩上的吸附属于物理吸附,这点在已有的研究中已得到证明；其次,该理论假设分子间的作用力为伦敦色散力,吸附势与温度无关,吸附特性曲线(纵坐标是吸附势,横坐标是吸附相体积)在任何温度下都一样[7]。因此，如若页岩的吸附符合吸附势理论,则其在不同温度下的吸附特性曲线应基本重合。这里选取30℃，60℃，90℃三个温度下的等温吸附数据来验证(见图2)。

吸附特性曲线由吸附势和吸附空间两个坐标组成。固体表面某点的吸附势定义为1mol气体从引力不起作用的气相被吸引到吸附相的某点所做的功,是温度和压力的函数：

(1)

式中:P为平衡压力,MPa;ε为吸附势,J/mol;P0为甲烷饱和蒸汽压力,MPa;Pi为理想气体在恒温下的平衡压力MPa;R为普氏气体常数,取值为8.314 472 J/(mol·K);T为绝对温度,K。

吸附特性曲线的另一个参数就是平衡条件下的吸附相体积,吸附相体积取决于被吸附气体的质量和气体出于吸附态时的密度:

(2)

式中:Vad为平衡条件下吸附相体积,cm3/g;m为吸附相气体质量,g;ρad为吸附相密度,g/cm3;V为测得的平衡条件下的气体吸附量,cm3。

关于吸附相密度的讨论见文献[8-9]。在实际计算吸附相密度中运用较多的公式是

ρad=ρbexp[-0.002 5×(T-Tb)]，

(3)

式中:ρb为沸点下甲烷密度,为0.142 4 g/cm3;Tb为甲烷沸点温度,为111.15K。

由公式(3)可见，吸附相密度主要受温度的控制。在实际计算中,甲烷吸附相密度常取为常数0.375 g/cm3,这里为计算方便也将甲烷吸附相密度取为0.375 g/cm3。

气体在实际储层中的温度远大于其临界温度,气体不能被液化,处于超临界状态,也就不存在公式(1)中的饱和蒸汽压。前人们提出用虚拟饱和蒸汽压来代表处于超临界状态气体的饱和蒸汽压,这时饱和蒸汽压是能使特征曲线的一个参数,并没有特定的物理意义。学者最常用的计算虚拟饱和蒸汽压公式是Dubinlin提出的[8],Amankwah改进了Dubinlin提出的公式,加入了与吸附体系有关的系数K，得到公式

(4)

式中：Pc和Tc分别表示临界压力和温度。

本文采取改进后的公式(4)。通过实验不同的K值,发现随着K值的增加,样品1的特征曲线相关系数都呈增加的趋势(见表2，图3)，除样品1在K=1的时候相关系数较小,其余的都超过了0.9,代入K=3时建立吸附特性曲线。因此可以看出,不同温度下特征曲线基本重合,特征曲线基本与温度无关,符合伦敦色散力的特性。当K=3时，两个样品的相关系数均超过了0.95,因此,在建立模型中,以K=3时的P0值来带入。

表2 K值和特征曲线的相关系数R2Tab.2 K and the correlation coefficient R2 of characteristic curve

图3 K=3时30℃，60℃，90℃时吸附特性曲线Fig.3 Adsorption curve at 30℃，60℃，90℃ when K=3

3 等温吸附曲线预测模型的建立和验证

吸附势与吸附相体积的关系为对数关系：

ε=alnVad+b。

(5)

公式(5)表示这一类曲线的大致形状,其中参数a,b是待定参数,其值可由拟合求得。

结合吸附势的表达式公式(1),可得到方程

(6)

联立表达式(2)，(4)，(6),经过整理后得到吸附量与温度、压力的关系式:

(7)

公式(7)只需由一组等温吸附数据就可以求得吸附势曲线及其表达式,得到参数a,b的具体值,也就可以得到吸附量与温度压力的关系式,也就可以用来预测任意温度压力下的吸附量。经过实际验算,预测值与实际测量的吸附量相差较大,因此在公式(7)中加入修正因子K0(这里K0取3)。加入修正因子后的模型,预测精度得到了很大提高，但修正因子的具体意义还有待研究。

由公式(7)可见,在温度一定的情况下,对压力P求导,可知吸附量与压力成正比。在压力一定的情况下,对温度函数T求导,可以得到吸附量与温度成反比,这与我们对吸附的认识是相吻合的。

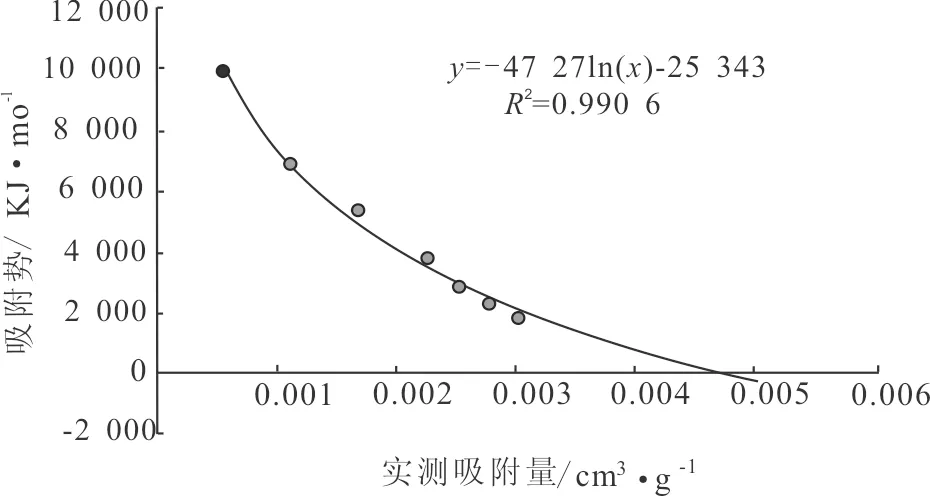
图4 样品在30℃时的吸附特性曲线Fig.4 Adsorption curve at 30℃

图4显示了由样品30℃时等温吸附曲线求得的吸附特性曲线,由拟合的吸附特性曲线求得a=4 727,b=25 343,带入公式(7)求出针对样品的预测模型。图5、图6显示了两个样品在60℃和90℃时,预测值与实际测得地吸附量的值的差异大小。在压力较小时,预测值与实际测量的吸附量相差不大,吸附模型能较好地预测吸附量。随着压力的增高,预测值与测量值的差异逐渐增加。

图4中吸附特性曲线延伸与吸附量轴相交,此时的吸附量为该页岩样品的极限吸附量。根据吸附势理论,多分子层吸附随着外层分子远离固体表面,吸附势逐渐降低。当吸附势为0时,固体表面不能再吸附任何气体分子,将此时的吸附相体积换算成正常状态下含气量即为饱和吸附气量,此时,无论压力如何再升高,吸附量不会再增加。经计算，该样品的吸附量为2.36 cm3·g-1。但实际上,鉴于页岩大量存在的纳米级孔隙,页岩孔隙内壁上所能吸附气体分子的层数是有限的,也就是说，没有等到最外层吸附分子的吸附势降为0,孔隙空间就已经被占满。因此,饱和吸附量会比用该方法求得的值要小。

针对随压力逐渐升高误差变大的现象,建议用数学里面的球状模型加以修正。因为从等温吸附曲线可以看出,在低压条件时,吸附量随着压力的增加也迅速增加,但压力增加到一定值的时候,吸附量的增加速度趋于平缓以至于不再增加,达到所谓的饱和状态。因此,这里有个压力界限值,可以用该界限值对应的吸附量作为最大吸附量从而对模型加以修正。采用数学里面的球形模型可以很好地计算出这个压力界限值。

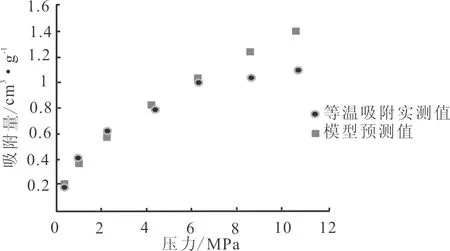
图5 样品在60℃时预测值与实测值Fig.5 Predictive value and true value at 60℃

图6 样品在90℃时预测值与实测值Fig.6 Predictive value and true value at 90℃

4 球形模型对最大吸附量的限定

球状模型(The spherical model)早在1960年由Matern提及,该模型的表达式为一个分段定义的非初等函数:

r(h)=C+C0h≥a,

r(h)=C0h=0。

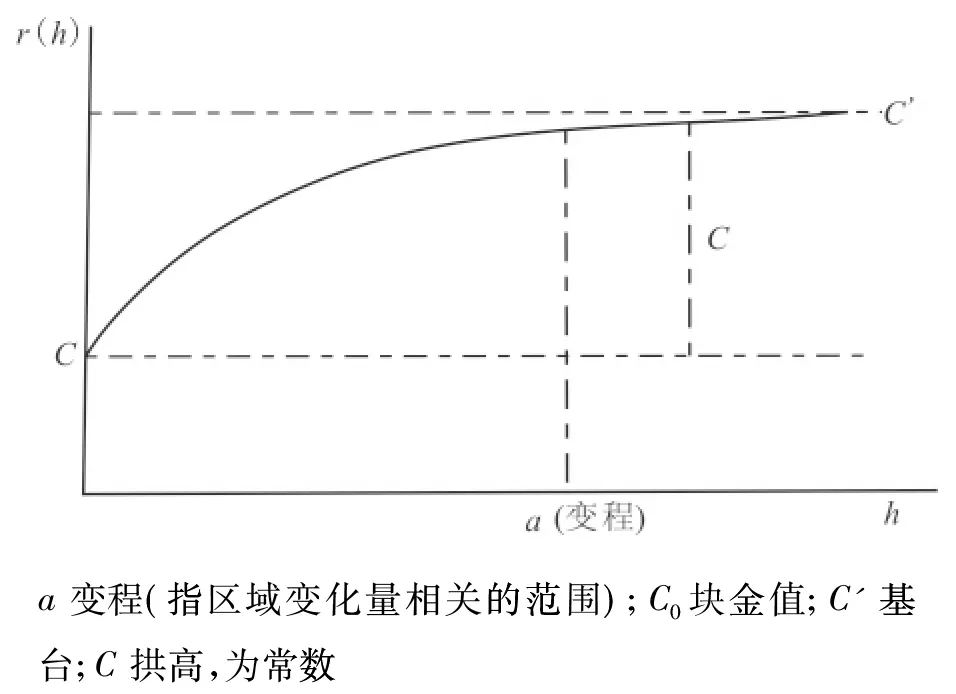
图7 球状模型变异曲线Fig.7 Spherical model variation curve

式中:a为变程(指区域变化量相关的范围);C0块金值;C′基台;C拱高,为常数。该模型很好地描述了等温吸附曲线的大致形状(虽然在h

5 结 论

1)根据页岩样品吸附特性曲线图,发现甲烷-页岩吸附特征曲线与温度无关,且属于物理吸附,能用吸附势定理建立吸附量随温度、压力变化的关系模型。

2)压力增高时,页岩吸附量随温度、压力变化的关系模型预测值与真实测量值间的差值增大,运用球状模型,能有效修正压力高点的误差。

3)在无吸附数据或者实验温度与储层实际温度不符的情况下,本模型对页岩储层资源量的预测、有利区的优选和储层特征描述有一定帮助。

[1] 刘洪林.中国南方海相页岩吸附特征及其影响因素[J].天然气工业,2012,32(9):5-9.

[2] KIM A G. Estimating Methane Content of Bituminouscoalbed from Adsorption Data[M].Washing to D C:US Bureau of Mine, 1977.

[3] 钟玲文,郑玉柱,员争荣,等.煤在温度和压力综合影响下的吸附性能及气含量预测[J].煤炭学报，2002,27(6):581-585.

[4] 赵志根, 唐修义. 较高温度下煤吸附甲烷实验及其意义[J].煤田地质与勘探，2001, 29(4): 29-30.

[5] 胡涛, 马正飞, 姚虎卿. 吸附热预测吸附等温线[J].南京工业大学学报, 2002,24(2):24-38.

[6] 近藤精一,石川达雄，等.吸附科学[M].北京工业出版社,2005:49-50.

[7] 顾惕人,朱步瑶,李外郎,等.表面化学[M]. 北京：北京科学出版社,2001:275-280.

[8] DUBININ M M. Thepotentialtheoryofadsorptionof gasesandvapors for adsorbents with energetically nonuniformsurfaces[J].Chem Rev,1960, 60: 235-2411.

[9] SKUSUMI S, OGINO Y J. Physical adsorptionofgasesathighpressures(IV): Animprovement of the Dubinin-Astakhovadsorptionequation[J]. Colloid&In-terface Science, 1976, 56: 83-911.

(编 辑雷雁林)

The adsorption capacity predicting model of shale gas under doubles variables of temperature and pressure

LI Xin1,2,3, JI Kun2,3, FANG Chao-qiang2,3, LIU Peng2,3, LI Bing2,3

(1.Department of Geology, Northwest University, Xi′an 710069, China; 2.Technical Center,China Petroleum Logging CO.LTD., Xi′an 710077, China, 3.The Logging Key Laboratory, CNPC, Xi′an 710077， China)

Calculating the shale′s adsorption capacity in reservoir′s temperature and pressure condition has a significant meaning for reservoir description and reserve estimate. The test of shale sample has shown that adsorption characteristic curves at different temperature levels are nearly coincidence. Combined with that adsorption between shale and methane is physical adsorption, adsorption potential theory can be used here to describe shale′s adsorption behavior. Then, by using adsorption data at 30℃, the model which can predict adsorption capacity at different temperature and pressure is built. By comparing adsorption data which are collected at 60℃ and 90℃ using this model, the fact has been founded that the accuracy of this model is becoming lower when pressure is higher.

shale gas; adsorbed gas; adsorption potential theory; adsorption characteristic curves; saturation absorptive capacity

2014-07-17

中国石油天然气集团公司科学研究与技术开发基金资助项目(2014A-3914)

李新，男，河南南阳人，高级工程师,西北大博士生,从事岩石物理性质及测井方法研究。

TE122.1

：ADOI：10.16152/j.cnki.xdxbzr.2015-03-018