三维脑部电阻抗成像技术研究

闫丹丹,沈圣远,李怀明

(中国计量学院 信息工程学院,浙江 杭州 310018)

三维脑部电阻抗成像技术研究

闫丹丹,沈圣远,李怀明

(中国计量学院 信息工程学院,浙江 杭州 310018)

电阻抗成像(electric impedance tomography,EIT)是利用测量得到边界电压重构内部电导率分布的技术.通过在ANSYS中建立三维头球模型并注入电流,采用自适应局部增强微分进化算法进行逆问题重构.首先对EIT的基本原理进行阐述，其次介绍微分进化算法在电阻抗成像中的应用，最后通过在头球模型上进行仿真实验,针对基本微分进化算法及其改进算法进行逆问题重构.仿真结果表明,改进的算法较微分进化算法在时间上有显著提高,适应性与牛顿-拉斐逊算法相比明显提高.

电阻抗成像;有限元分析;头模型;微分进化算法

EIT是一种利用边界电势推导内部电导率分布的功能性成像技术.EIT采用体表注入电流的测量方式获取电压,其测量数据提供的目标区域的边界信息较多[1].

EIT将电极以特定的方式放置在对象表面,选取合适的电极分布.相对注入方式具有良好的信噪比,在相对注入模式下通过相对电极测量方式测量电压,能够测得电流最大限度通过对象内部[2-4],获得最佳的测量效果,因此一般选用相对注入方式.

在人体头部组织未发生器质性病变之前,传统的成像手段难以检测.EIT以电导率为成像介质,能够在未发生形态学变化之前检测出颅内电导率的变化.目前的重构算法中比较成熟的EIT重构算法有Newton类算法、双限定算法、扰动算法和微分进化等算法.由于微分进化算法原理简单,具有高效性、收敛性、鲁棒性等优点，故本研究采用微分进化算法.

1 EIT成像原理

1.1 EIT正问题计算

EIT仿真研究分为正问题求解和逆问题重构.正问题的求解是逆问题重构的前提,正问题求解假设已知电导率σ的分布,求解电导率分布.正问题的数学模型如下:

(1)

式(1)中，φ—边界电压值,σ—电导率.

1.2 EIT逆问题求解

EIT分为静态成像和动态监测,动态成像是以电导率的相对值作为成像目标[5].动态成像以电导率差值重构图像,实时性较强.静态成像则是以电导率的绝对值为目标,本研究以静态成像为主,静态成像的电导率σ求解公式如下:

▽(σ(x,y)▽φ(x,y))=0 (x,y)∈∂Ω;

(2)

σ(x,y)·∂φ(x,y)·(∂n)-1=j(x,y)
(x,y)∈∂Ω.

(3)

式(2)(3)中，∂Ω—目标区域的边界,φ(x,y)—测得的体表电势,j(x,y)—该流过该区域的电流密度.

由于电流注入方式有限、测量电极有限,因此EIT求解存在非线性和病态性问题[6].在实际应用中可将逆问题求解转化为求解边界电压的测量值与估计电导率值之间差值的最小化问题[7].求解如下:

f(σ)=[φ(σ)-φ0]T[φ(σ)-φ0].

(4)

式(4)中，σ—电导率,f(σ)—边界电压的测量值与模拟值的差值.求解出最符合条件的f(σ)最小值[8],得出电导率分布的近似解.

2 微分进化算法

微分进化算法(differential evolution algorithm, DE)是基于生物进化理论的算法.该算法具有并行区域搜索的优点,利用种群个体的随机扰动产生下一代种群个体,记录最优的参数向量[9],最终得到收敛较好的解.

2.1 微分进化算法

由于逆问题求解的病态性,将逆问题转化为利用算法迭代求解函数f(σ)的最小值.微分进化算法操作如下:

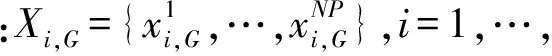
(5)

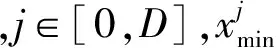
2)变异 变异算子是选取当前种群中的两个及两个以上的随机个体做差,并乘以控制参数F.变异算子分为以下5种.

①DE/best/1:

vi,G=xbest,G+F(xr2,G-xr3,G);

②DE/rand/1:

vi,G=xr1,G+F(xr2,G-xr3,G);

③DE/rand-to-best/1:

vi,G=vi,G+F1(xbest,G-xi,G)+F2(xr1,G-xr2,G);

④DE/best/2:

vi,G=xbest,G+F(xr1,G+xr2,G-xr3,G-xr4,G);

⑤DE/rand/2:

vi,G=xr1,G+F(xr2,G+xr3,G-xr4,G-xr5,G).

r1,r2,r3,r4,r5∈[1,…NP],表示种群中个体的的序列值,F为放大系数,xbest,G为G代种群中的最优值,vi,G表示变异之后的种群个体值.

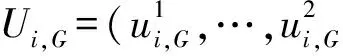
(6)

式(6)中，randj(1,1)—[0,1]之间第j个随机数的估计值,Pc—交叉概率,jrand∈[1,D]—随机电导率值.

4)选择 将中间向量带入目标函数进行比较,选中具有较小目标函数值的个体[11],作为下一代种群的搜索起始点.

5)边界处理 限制电导率σ在约束范围之内.边界约束公式如下：

(7)

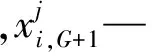
2.2 改进微分进化算法

微分进化算法在寻优过程中,参数选取根据进化速度作适应性调整,能够提高算法的收敛速度.

对缩放因子F、交叉概率Pc做适应性调整,

调整公式如下:

(8)

(9)

式(8)(9)中，F(0)和Pc(0)—在迭代过程中的初始值,Pcmin、Fmax—前n次进化过程中最大值和最小值,Gmax—最大进化数.

3 仿真研究和结果分析

3.1 仿真研究

本研究采用三层均质头球模型.模型分为头皮、颅骨、颅内部分和病变部分.根据先验知识可知,在颅内病变部位的电导率值会有所变化[12],因此在本次试验中将各组织电导率按比例设置为头皮∶颅骨∶颅内部分∶病变部分=1∶15∶1∶2.

在ANSYS中对建立三维头部球模型,假设头部为均质的各向同性导体[13].采用16电极相对电极注入±5 mA电流.图1表示病变组织位于不同位置时的真实电导率分布图.

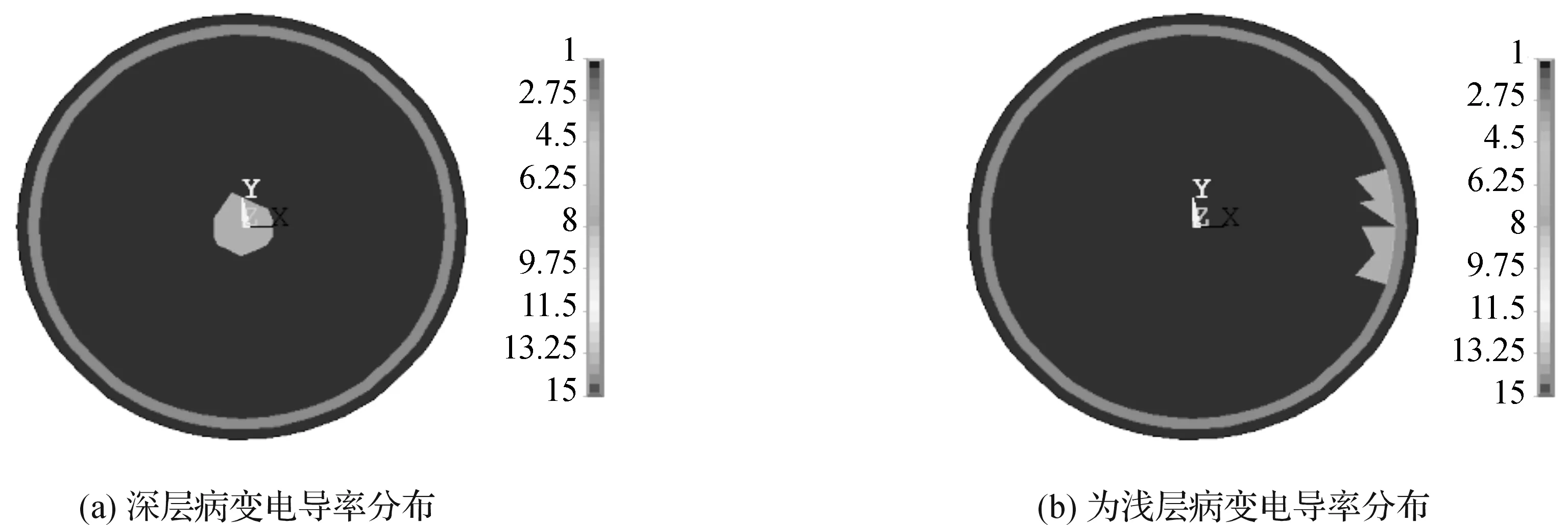
图1 头部模型电导率真实分布Figure 1 Conductivity distribution of head model

3.2 结果分析

误差总和TE进行定量的结果分析.计算公式如下:

(10)

式(10)中，ρest和ρtrue—重构(估计)电导率和真实电导率,m—电导率σ的自由度.

本实验将种群的数量为80,F、Pc分别为0.5、0.9.终止条件:20次迭代或目标函数f(σ)的值小于10-6.利用算法的三种策略重构电导率分布.重构效果如图2,数据如表1.

表1 迭代次数一定的条件下三种策略的重构结果比较(病变组织位于大脑内部)

Table 1 Comparison of the reconstruction results of three strategies under the certain iterations conditions(diseased tissue located inside the brain)

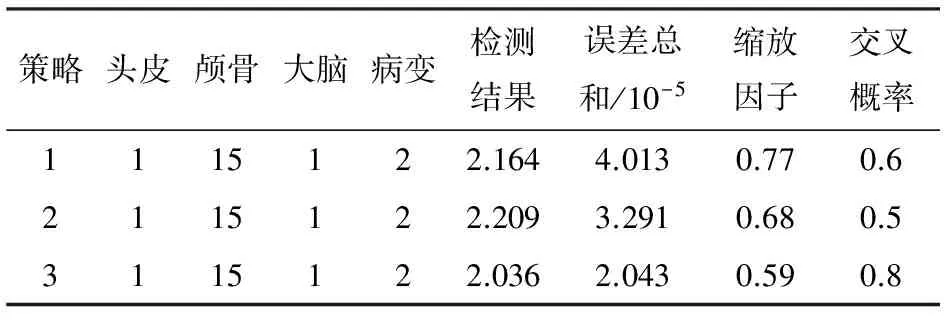
策略头皮颅骨大脑病变检测结果误差总和/10-5缩放因子交叉概率1115122．1644．0130．770．62115122．2093．2910．680．53115122．0362．0430．590．8

图2 DE算法的三种策略重构图(病变组织位于大脑内部深处)Figure 2 Three map of reconstruction strategy of basic DE algorithm (diseased tissue located deep inside the brain)

取消迭代次数限制,种群数量和交叉系数以及放大系数的初始值保持不变.三种策略的重构图像如图3.

改进后算法与DE算法对深层病变检测的数据比较如表2.

通过对表1和表2的数据分析对比可知,改进算法在迭代次数一定时,策略3效果较好.对比F和Pc的值可知,在迭代终止时,策略3中F和Pc的值更加接近初始值,策略2中F的值较为接近初始值,策略1中Pc的最终值与初始值存在较小的差距.对病变组织位于颅骨边缘的情况进行仿真研究,如图4.

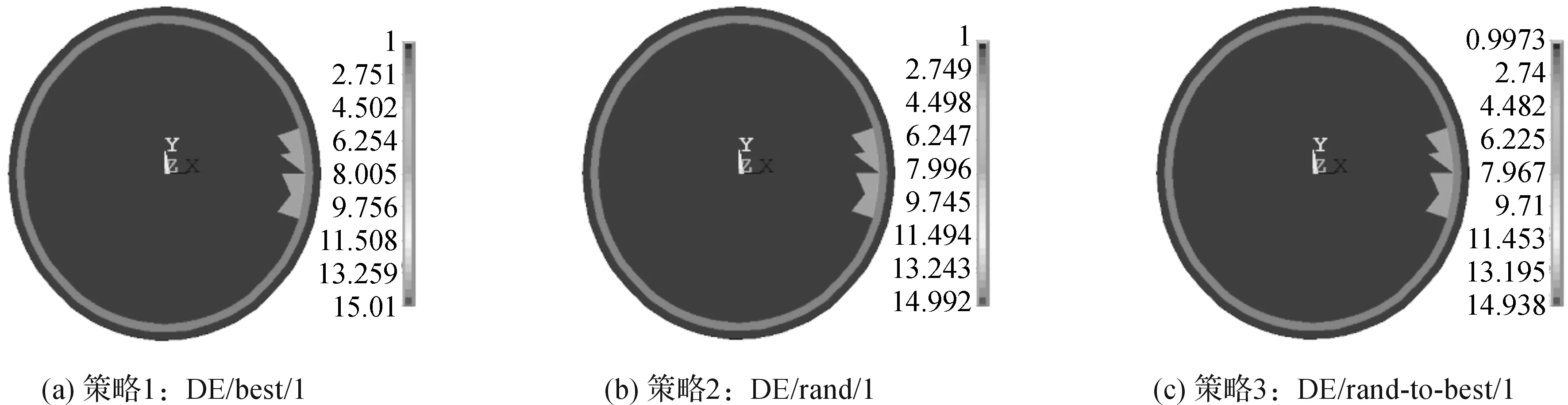
图4 脑内颅骨边缘病变检测Figure 4 Disease of edge skull brain lesion detection

仿真结果表明,DE算法在F和Pc为固定值的情况下,策略2效果较好.改进算法对深层和浅层病变仿真实验中均有明显的提升,但是在精度上有损失.因此，改进算法可以增加收敛的速度.

4 结 语

仿真结果表明,收敛速度加快.重构的电导率图像能对病变部位的大小、位置和分布情况作出准确判断.在进化过程内部完成对控制系数的适应性调整.该算法适应性较强也可以应用到其他的成像部位,由于肺部成像与头部的组织多样性有着相似性[14-15],因此算法可以用于对肺部成像.

算法在头部应用上存在成像时间过长的缺点,在EIT逆问题求解中需要对种群个体进行评价,计算时间较长.相比牛顿-拉斐逊算法省去了Jacobian的计算.牛顿-拉斐逊算法具有收敛速度快的优点,但是对迭代初始值要求比较苛刻,因此,将改进的算法与牛顿类算法结合可以克服两者的不足.

近年来,EIT成像技术有了很大的进步,但是其成像分辨率仍不能完全满足诊断的要求.在临床上,EIT的成像结果作为辅助手段仍需要硬件和软件等技术方面的突破.本研究利用微分进化算法作为逆问题重构算法,获取清晰的电导率图像,为医学临床诊断提供了一定的参考.

[1] 陈会,闫丹丹.基于磁共振技术的生物电阻抗成像技术研究进展[J].中国医学影像学杂志，2014(9):14-717. CHEN Hui, YAN Dandan. Research progress of bioelectri-cal impedance tomography based on magnetic resonance technology[J].Chinese Journal of Medical Imaging,2014(9):714-717.

[2] HARTINGER A E, GUARDO R,et al. EIT system and reconstruction algorithm adapted for skin cancer imaging[J].Information Science, Signal Processing and their Applications(ISSPA),2012(7):798-803.

[3] ZHAO Shu, DENG Juan, SHA Hong, et al. The impact of the measurement accuracy and the excitation pattern on EIT image reconstruction[J].International Conference on Biomedical Engineering and Informatics (BMEI),2013(12):59-63.

[4] CONSTANTINOU L, TRIANTIS I F, BAYFORD R, et al. Highpower cmos current driver with accurate trans-conductance for electrical impedance tomography[J].Biomedical Circuits and Systems,2014(2):1-9.

[5] MOURA F S, AYA C C, FLEURY A T, et al. Dynamic imaging in electrical impedance tomography of the human chest with online transition matrix identification[J].IEEE Transactions on Biomedical Engineering,2010(2):422-431.

[6] KURNIADI D, RANUDDIN M, MAULAN A A. Fuzzy assisted parameter selection rule in regularized newton algorithm of electrical impedance tomography[J].Information Technology and Biomedical Engineering,2011(11):1-4.

[7] 杨琳,徐灿华,付峰,等.一种基于加权频差阻尼最小二乘的准静态EIT算法[J].仪器仪表学报,2013(8) :1879-1885. YANG Lin, XU Canhua, FU Feng,et al. Quasi-static EIT algorithm based on weighted frequency difference damped least square[J].Chinese Journal of Scientific Instrument,2013(8):1879-1885.

[8] Md. ISLAM R, Md. KIBER A. Electrical impedance tomography imaging using gauss-newton algorithm[J].International Conference on Informatics,2014(3):1-4.

[9] 黄仁全,靳聪,贺筱军,等.自适应局部增强微分进化改进算法[J].空军工程大学学报:自然科学版,2011(3):6,83-88. HUANG Renquan, JIN Cong, HE Xiaojun, et al. Adaptive local enhancement and differential evolution algorithm[J].Journal of Air Force Engineering University: Natural Science Edition,2011(3):83-88.

[10] RIBEIRO R R, FEITOSA A R S, SOUZA R E, et al. Reconstruction of electrical impedance tomography images using genetic algorithms and non-blind search[J].Biomedical Imaging (ISBI),2014(5):153-156.

[11] 李颖,徐桂芝,饶利芸,等.微分进化算法在头部电阻抗成像中的应用[J].中国生物医学工程学报,2005(6):672-675. LI Ying, XU Guizhi, RAO Liyun, et al. Application of DE algorithm for brain imaging using EIT[J].Chinese Journal of Biomedical Engineering,2005(6):672-675.[12] FEITOSA R S, RIBEIRO R R, BARBOSA V F, et al. Reconstruction of electrical impedance tomography images using particle swarm optimization, genetic algorithms and non-blind search[J].Biosignals and Robotics for Better and Safer Living (BRC),2014(5):1-6.

[13] 闫丹丹,陈会.基于电阻抗成像技术的脑病变组织检测仿真研究[J].中国医学影像技术,2014(7):1113-1116. YAN dandan, CHEN Hui. Detection of brain anomaly based on electrical impedance imaging simulation research[J].Chinese Journal of Medical Imaging Technology (CJMIT),2014(7):1113-1116.

[14] HAMILTON S J, MUELLER J. Direct EIT reconstructions of complex admittivitieson a chest shaped domain in 2D[J].IEEE Trans Med Imaging,2013(4):757-769.

[15] BOVERMAN G, KAO T. KULKARNI R, et al. Robust linearized image reconstruction for multi-frequency EIT of the breast[J].Medical Imaging,2008(10):1439-1446.

Electric impedance tomography imaging study based on the differential evolution algorithm

YAN Dandan, SHEN Shengyuan, LI Huaiming

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

Electric Impedance Tomography(EIT) is the technology that obtains internal conductivity distribution reconstruction with the voltage of the boundary of the study object. A three-dimensional model of head was created in the software of ANSYS and was injected current to reconstruct the inverse problem using the local enhancement self-adaptive differential evolution algorithm. The inverse problem was reconstructed with the basic differential evolution algorithm and the improved algorithm on the model in the experiment.The results indicate that the adaptability and the speed of the novel algorithm are improved significantly than that of the differential evolution algorithm and the Newton-Raphson algorithm.

electrical impedance tomography; ANSYS; head mode; differential evolution algorithm

1004-1540(2015)03-0331-05

10.3969/j.issn.1004-1540.2015.03.015

2015-03-18 《中国计量学院学报》网址：zgjl.cbpt.cnki.net

闫丹丹(1979- )，女，吉林省舒兰人，副教授，主要研究方向为MRI的生物医学电阻抗成像、生物医学图像处理以及基于有限元方法的生物模型建模．E-mail：dandanyan@cjlu.edu.cn

TP39;R3

A