基于传输矩阵法的纵向啁啾体光栅衍射特性
2015-02-26王军阵,汪岳峰,白慧君
基于传输矩阵法的纵向啁啾体光栅衍射特性
王军阵,汪岳峰*,白慧君
(军械工程学院 电子与光学工程系,石家庄 050003)
摘要:为了研究纵向啁啾体光栅的光谱衍射特性,采用传输矩阵方法进行了分析,研究了光栅的厚度、折射率调制系数和啁啾波长范围对纵向啁啾体光栅中心衍射效率的影响。结果表明,随着光栅厚度的增加,中心衍射效率随之增大;随着光栅折射率调制系数的增大,中心衍射效率也随之逐渐增加;而随着啁啾波长范围的增大,纵向啁啾体光栅的中心衍射效率则逐渐减小。此研究结果对大尺寸啁啾体光栅的设计制作有一定的参考价值。
关键词:衍射;纵向啁啾体光栅;传输矩阵法;衍射效率
*通讯联系人。E-mail:wyfmail@sina.com
引言
在激光系统的设计中使用衍射光学元件(全息体光栅),通常被认为是一种改善激光光束质量、降低系统体积和重量的有效方法。记录在光致热敏折射率(photo thermal refractive,PTR)玻璃中的体光栅作为一种体衍射光学元件具有热稳定性好、线性传输特性、高分辨率、损伤阈值高等优点,在高功率激光器的光谱合成、角度选择近场滤波和二极管激光器输出光谱稳定以及模式选择中有着非常重要的应用[1-4]。近年来,一种新型的大尺寸纵向啁啾体光栅在啁啾脉冲放大等领域的应用取得了明显的效果。1998年,GALVANAUSKAS将一块200μm×300μm×5mm的纵向啁啾体光栅应用在啁啾脉冲放大领域,实现了500nJ的脉冲能量输出[5]。随后,许多学者[6-9]将大尺寸纵向啁啾体光栅应用于不同波段的啁啾脉冲放大系统中,取得了非常好的效果。参考文献[10]和参考文献[11]中分别从解析方法分析了纵向啁啾体光栅的衍射特性,参考文献[12]中系统地阐述了传输矩阵法在求解常规体光栅衍射特性中的应用,参考文献[13]中提出了用于分析常规体光栅衍射特性的传输矩阵法[14],这种方法还可以用于啁啾体光栅衍射特性分析[15]。本文中介绍了一种用于分析纵向啁啾体光栅的传输矩阵方法,将纵向啁啾体光栅进行分片处理后,采用传输矩阵方法,数值计算了啁啾体光栅的光谱衍射特性,研究了纵向啁啾体光栅的厚度和折射率调制系数对中心波长处衍射效率的影响,分析了啁啾波长范围与纵向啁啾体光栅中心波长处衍射效率的关系。
1理论分析
纵向啁啾体光栅衍射示意图如图1所示,入射光束的波长不同,在纵向啁啾体光栅内部发生衍射的位置也会不相同,中心波长分别为λ1和λ2的两束单色平面波,当以完全满足各自的布喇格条件以θi角入射时,会在具有高衍射效率的纵向啁啾体光栅的不同深度分别以θo角被衍射,在图1中,设纵向啁啾体光栅中心位置的周期为Λ0,则光栅中心位置的空间频率可表示为f0=1/Λ0,光栅的厚度为t,光栅的折射率沿表面法线z方向的分布可表示为:

式中,n0表示光栅的背景折射率;Δn表示折射率调制系数;Q表示纵向啁啾体光栅中心位置的光栅矢量,方向垂直于光栅中折射率为常数的平面,其大小为2π/Λ0;γ(z)为啁啾体光栅的相移(啁啾函数)。
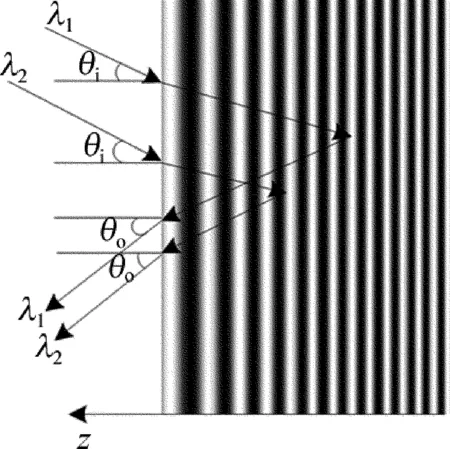
Fig.1 Diffraction scheme of longitudinal chirped volume Bragg gratings
利用KOGELNIK的耦合波理论[16]或严格耦合波理论[17]可方便地分析常规体光栅的光谱衍射特性,但对于纵向啁啾体光栅,由于沿光栅z方向的折射率调制周期不再是固定不变的常数,以上两种理论将不再适用于分析纵向啁啾体光栅的光谱衍射特性,传输矩阵方法可以分析任意体光栅的光谱衍射特性,其将体光栅沿z方向的每个周期固定地分为N个薄层,光栅的每个周期内分层的数目越多,计算结果的精度就会越高[18]。当入射光以波长λ入射至纵向啁啾体光栅表面时,则光波在第i层的特征矩阵为:

式中, δi=(2π/λ)nidicosθi,其中λ为入射光束的波长,ni和di分别为第i层的折射率和厚度,θi为入射光束在进入第i层介质时的入射角,ηi为第i层的有效导纳,当入射光波为s偏振(振动方向与入射面垂直)时,ηi=nicosθi,当入射光波为p偏振(振动方向与入射面平行)时,ηi=ni/cosθi。
当光通过N层介质后,总的特征矩阵为:


式中,M11,M12,M21和M22分别表示各矩阵乘积所得矩阵对应的矩阵元。
则当光通过N层介质后的振幅反射系数为:
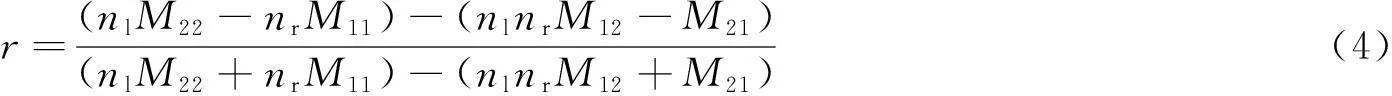
式中,nl,nr分别表示光栅前后面的折射率。
则光栅的衍射效率为:

式中,r表示纵向啁啾体光栅对光的振幅反射系数,r*表示r的共轭。
2数值计算和分析
以衍射波长在980nm附近为例分析纵向啁啾体光栅的光谱衍射特性,取纵向啁啾体光栅的厚度为30mm,背景折射率为1.5,折射率调制系数为6.7×10-4,啁啾波长范围为10nm,将纵向啁啾体光栅进行分层处理,为简化计算,设入射光的入射角为0,每个光栅周期固定分30层,采用传输矩阵方法求得的纵向啁啾体光栅的光谱衍射特性如图2所示。

Fig.2Diffraction efficiency vs. wavelength of chirped volume Bragg gratings
从图2中可以看出,啁啾体光栅的中心衍射效率为99.1%,在其整个通带与阻带上都有较小的波动,波纹小于0.3%,采用切趾或提高体光栅的光谱衍射效率的方法,可从一定程度上减弱这种波动性。这与啁啾光纤光栅的光谱衍射特性基本相同,但与光纤光栅相比,纵向啁啾体光栅具有尺寸大小可定制和在高功率情况下具有更好的耐热性等优点。
图3中给出了背景折射率为1.5、折射率调制系数为6.7×10-4、啁啾波长范围固定为10nm时,纵向啁啾体光栅的厚度与中心衍射效率的关系曲线。从图中可以看出,在厚度小于10mm时,随着厚度的增加,衍射效率得到了迅速提升。而当厚度大于10mm时,由于衍射效率逐渐趋近于1,其提升效果变得缓慢,因此,通过增加厚度可以提高衍射效率,在较高衍射效率时,通过增加厚度来提高衍射效率的效果越来越不明显。
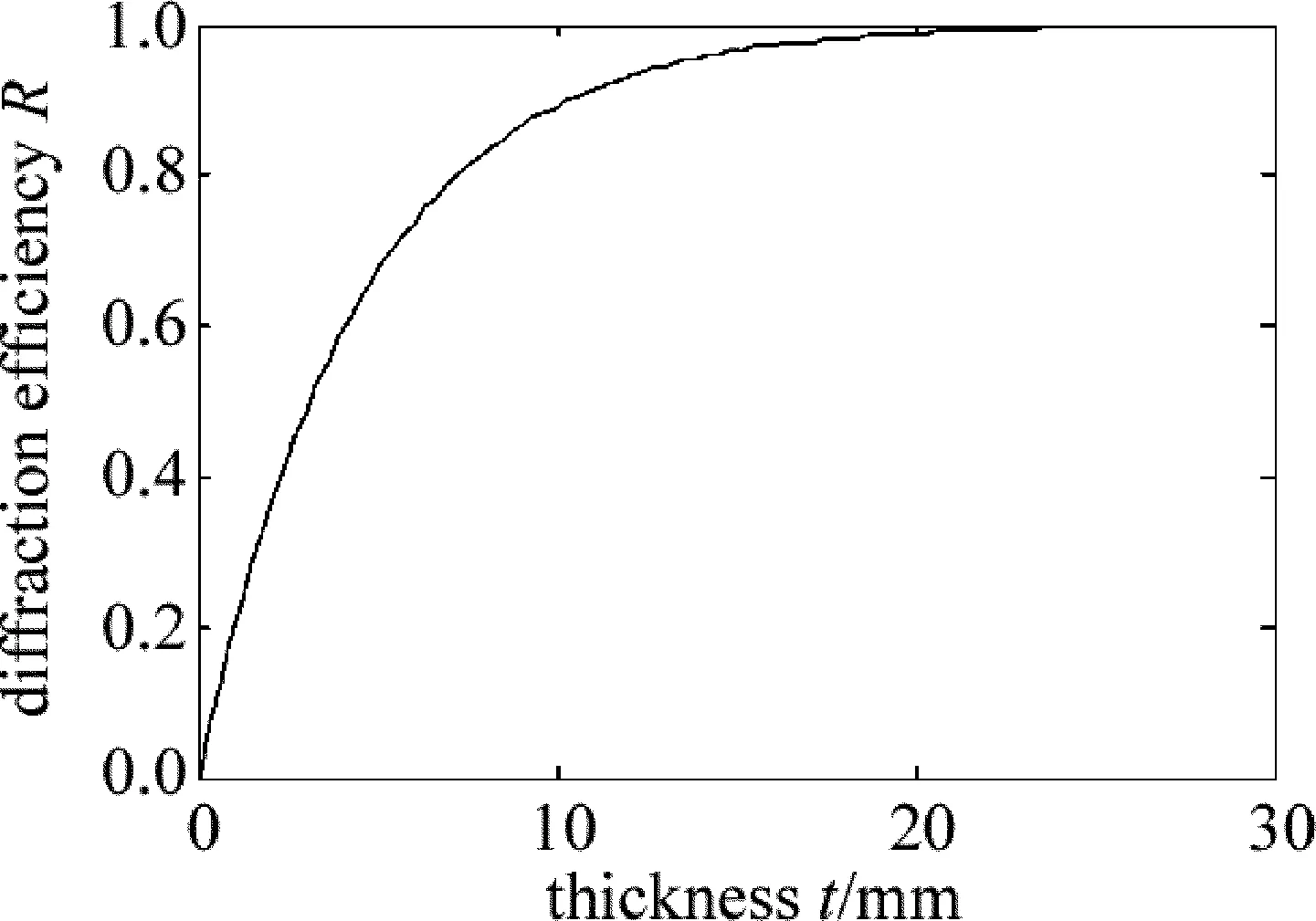
Fig.3 Diffraction efficiency vs. thickness
图4中给出了背景折射率为1.5、厚度为30mm、啁啾波长范围为10nm时,纵向啁啾体光栅的折射率调制幅值与中心衍射效率峰值的关系。由图4可以看出,当折射率调制幅值为1×10-4时,啁啾体光栅的中心衍射效率仅为15%,当折射率调制幅值在1×10-4与4×10-4之间时,随着折射率调制幅值的增大,中心衍射效率呈近似线性增大,而当折射率调制幅值大于4×10-4时,由于中心衍射效率趋近于1,这时,随着折射率调制系数的增大其也开始缓慢增大。因此,制作啁啾体光栅时,通过选用合适的折射率调制系数,可以获得所需要的中心衍射效率。

Fig.4 Diffraction efficiency vs. refractive index modulation
图5中给出了背景折射率为1.5、厚度为10mm、折射率调制系数为6.7×10-4时,纵向啁啾体光栅的啁啾波长范围对中心衍射效率的影响。从图5中可以看出,啁啾波长范围在0nm~25nm时,纵向啁啾体光栅的中心衍射效率大于90%,在此区间对衍射效率变化较小,当继续增大啁啾波长范围时,啁啾波长范围在25nm~150nm之间时,中心衍射效率随之迅速下降,此时,中心衍射效率变化较大,而在150nm以后继续变大时,中心衍射效率下降开始变得非常缓慢,对中心衍射效率的影响越来越小。
综合图3~图5中啁啾体光栅厚度、折射率调制系数和啁啾波长范围对光栅中心衍射效率的影响可知:纵向啁啾体光栅中心的衍射效率随着光栅厚度和折射率调制系数的增加而增加,随光栅的啁啾波长范围的增大而减小。因此,可以通过选用合适的光栅厚度和折射率调制系数,来制作不同啁啾波长范围和不同中心衍射效率的纵向啁啾体布喇格光栅。
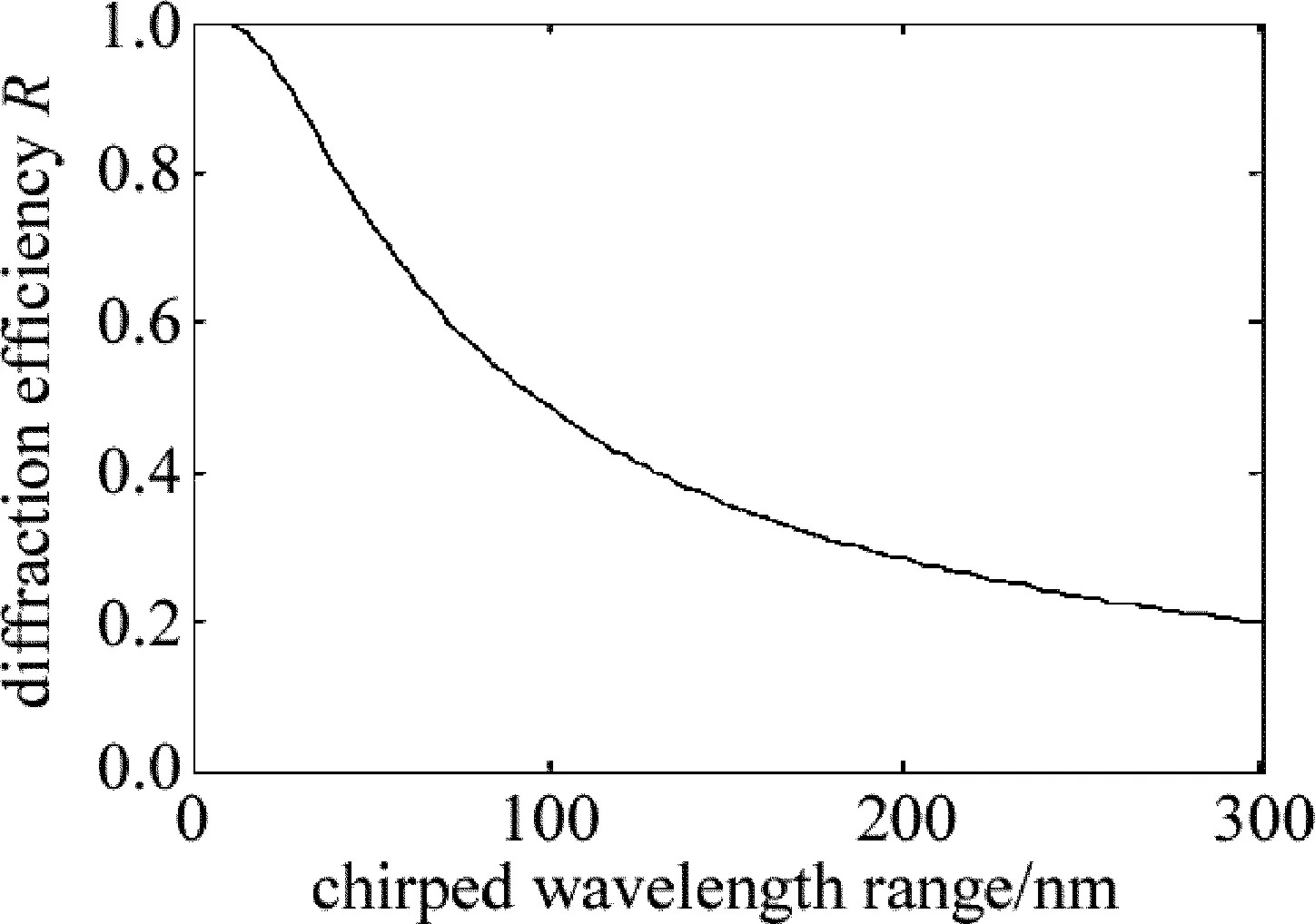
Fig.5 Diffraction efficiency vs. chirped wavelength range
3结论
介绍了一种数值求解纵向啁啾体光栅的传输矩阵方法,利用这种方法计算了纵向啁啾体光栅的光谱衍射特性,分析了光栅厚度、折射率调制系数对中心衍射效率的影响,研究了啁啾波长范围与中心衍射效率的关系。结果表明,随着光栅厚度的增大,中心衍射效率随之升高;随着光栅折射率调制系数的增大,中心衍射效率也随之升高;而随着啁啾波长范围的增大,中心衍射效率随之降低。可以通过选定不同的光栅厚度与折射率调制幅值,实现不同的衍射效率和啁啾波长范围的纵向啁啾体光栅,这对大尺寸啁啾体光栅的制作有一定的指导意义。
参考文献
[1]WANG J Z, WANG Y F, BAI H J. Study on multi-channel spectral beam combined characteristics based on volume Bragg gratings[J]. Laser Technology, 2012, 36(5):593-596(in Chinese).
[2]LIU B, LI J. Study about spectral beam combining with volume Bragg grating by means of Gaussian apodization technique[J]. Laser Technology, 2013, 37(5):656-659(in Chinese).
[3]PABOEUF D, VIJAYAKUMAR D, JENSEN O B,etal. Volume Bragg grating external cavities for the passive phase locking of high brightness diode laser arrays: theoretical and experimental study[J]. Journal of the Optical Society of America, 2011, B28(5):1289-1299.
[4]VENUS G B, SEVIAN A, SMIRNOV V I,etal. High brightness narrow line laser diode source with volume Bragg grating feedback[J]. SPIE, 2005, 5711:166-176.
[5]GALVANAUSKAS A, HEANEY A, ERDOGAN T,etal. Use of volume chirped Bragg grating for compact high-energy chirped pulse amplification circuits[J].Lasers and Electro-optics, 1998, 6(3):362.
[6]GLEBOV L B, GLEBOVAL L N, SMIRNOV V I,etal. Laser damage resistance of photo-thermo-refractive glass Bragg gratings[J]. Proceedings of Solid State and Diode Lasers Technical Review, 2004, 15(6):3-6.
[7]LIAO K H, CHENG M Y, FLECHER E,etal. Large-aperture chirped volume Bragg grating based fiber CAP system[J]. Optics Express, 2007, 15(8):4876-4882.
[8]CHANG G Q, LIU Ch H, LIAO K H,etal. 50W chirped volume Bragg grating based fiber CPA at 1055nm[C]//Conference on Lasers and Electro-optics/Quantum Electronics and Laser Science Conference and Photonic Applications Systems Technologies. Baltimore,New York,USA:IEEE, 2007:1-2.
[9]CHANG G Q, REVER M, SMIRNOV V,etal. 32W femtosecond Yb-fiber CPA system based on chirped volume Bragg gratings[C]//Conference on Lasers and Electro-optics/Quantum Electronics and Laser Science Conference and Photonic Applications Systems Technologies. Baltimore,New York,USA:IEEE, 2008:1-2.
[10]GLEBOV L B, MOKHOV S V, SMIRNOV V I,etal. Analytic theory of light reflection from a chirped volume Bragg grating[C]//Novel Optical Architectures in Emerging Technologies Ⅱ. San Jose,USA: Frontiers in Optics, 2009:5.
[11]BELAI O V, PODIVILOV E V, SHAPIRO D A. Group delay in Bragg grating with linear chirp[J]. Optics Communications, 2006, 266(2):512-520.
[12]GLEBOV L B, LUMEAU J, MOKHOV S,etal. Reflection of light by composite volume holograms: Fresnel corrections and Fabry-Perot spectral filtering[J]. Journal of the Optical Society of America, 2008, 25(3):751-764.
[13]MOHARAM M G, GAYLORD T K. Chain-matrix ayalysis of arbitrary-thickness dielectric reflection gratings[J]. Journal of the Optical Society of America, 1982, 72(2):187-190.
[14]SHARLANDJIEV P, MATEEVA T. Normal incidence holographic mirrors by the characteristic matrix method: numerical examples[J]. Journal of Optics, 1985, 16(4): 185-189.
[15]FENG J S, YUAN X, ZHANG X,etal. Simulation of chirped volume Bragg grating with a partition integration method[C]//Progress In Electromagnetics Research Symposium Proceedings. Suzhou, China: Soochow University, 2011:1295-1298.
[16]KOGELNIK H. Coupled wave theory for thick hologram gratings[J]. The Bell System Technical Journal, 1969, 48(9) :2909-2947.
[17]MOHARAM M G, GAYLORD T K. Rigorous coupled wave analysis of planar grating diffraction[J]. Journal of the Optical Society of America, 1981, 17(7):811-818.
[18]McCARTNEY D J. The analysis of volume reflection gratings using optical thin-film techniques[J]. Optical and Quantum Electronics, 1989, 21(2):98-107.
Diffraction characteristics of longitudinal chirped volume
grating based on transfer matrix algorithm
WANGJunzhen,WANGYuefeng,BAIHuijun
(Electrics & Optics Engineering Department, Ordnance Engineering College, Shijiazhuang 050003, China)
Abstract:In order to study diffraction characteristics of longitudinal chirped volume Bragg gratings, transfer matrix algorithm was used. Effects of the thickness, refractive index modulation and chirped wavelength range on the central diffraction efficiency of the longitudinal chirped volume Bragg gratings were calculated. The results show that central diffraction efficiency increases with the increase of the thickness and the refractive index modulation of the Bragg grating. However, with the increase of the chirped wavelength range, the central diffraction efficiency decreases. The research results have certain reference value for design and manufacture of large size of chirped volume Bragg gratings.
Key words:diffraction; longitudinal chirped volume grating; transfer matrix algorithm; diffraction efficiency
收稿日期:2014-01-03;收到修改稿日期:2014-01-20
作者简介:王军阵(1984-),男,博士研究生,主要研究方向为激光合成等方面。
中图分类号:O436.1;TN253
文献标志码:A
doi:10.7510/jgjs.issn.1001-3806.2015.01.012
文章编号:1001-3806(2015)01-0061-04 1001-3806(2015)01-0065-06
