用于梳状结构光学测速系统的周期优化方法
2015-02-26张春熹周金男
罗 娜,欧 攀,张春熹,周金男
(北京航空航天大学 仪器科学与光电工程学院, 北京 100191)
用于梳状结构光学测速系统的周期优化方法
罗娜,欧攀*,张春熹,周金男
(北京航空航天大学 仪器科学与光电工程学院, 北京 100191)
摘要:为了提高梳状结构光学测速系统的测速精度,采用数学原理研究了梳状结构的间距大小对输出光强信号周期性的影响,通过优化输出光强信号的周期性来提高测速精度,并采用一种结合图像处理选择最佳间距的实验方法,进行了相关的理论分析,对两种不同路面进行了实验仿真验证,得到不同间距下不同的输出光强信号的周期性情况。结果表明,当栅状结构的间距大小与地面特征点大小一致时,得到的输出光强周期性最优,对于普通的柏油和水泥路面,对应到地面的最佳栅状结构间距大小为1.0mm ~1.5mm。
关键词:测量与计量;周期优化;图像处理;梳状结构;差分输出
*通讯联系人。E-mail:oupan@buaa.edu.cn
引言
近年来,光学非接触式测速方法由于克服了接触式测量容易产生形变误差的缺点,同时具有测量精度较高,对测量目标表面要求较低等优点,成为了常用的测速方法之一[1]。光学非接触测量方法包括激光多普勒测速方法[2-3]、雷达测速方法、全球定位系统(global positioning system,GPS)测速方法以及基于梳状结构的测速方法[4]等。基于梳状结构的光学测速方法主要利用空间滤波原理进行速度测量,测量设备一般安装在车身并随车一起运动,地面杂乱花纹的反射光进入该测量系统,在光电器件上成像并扫描梳状结构,经过空间滤波等处理后被探测器接收。探测器输出周期变化的光强信号,其周期数与被测物体的速率成正比,通过测量某段时间内光强信号的周期数即可由公式实时计算速度[5-6]。
本文中主要从优化输出光强信号周期性的角度来提高测速精度,先从理论上分析了梳状结构的间距大小与输出光强信号周期性之间的关系,再对两种不同路面进行实验分析,结合图像处理的方法对不同条纹间距下输出光强信号的周期性进行比较,从而确定了最佳的条纹间距大小选择,为实际系统中梳状结构的间隔大小选择提供参考。
1光学非接触测速方法的介绍
1.1 梳状结构与速度测量的数学原理
基于梳状结构的光学测速方法是通过空间滤波原理实现速度测量[7-8],假设某特征点在梳状结构平面上运动,如图1所示。该特征点从左向右运动经过梳状结构,当特征点处在梳状结构间隙时,光强最强,当特征点处在梳状结构处时,光强最弱,由于梳状结构的重复性,若对梳状结构后的光强信息进行采集,光强会出现周期性的变化,且一个周期对应特征点经过一对梳状结构。

Fig.1 Principle of spatial filtering velocimety
若该特征点以速率v(m/s)从左向右经过梳状结构,运动t(s)时间,移动长度为l(m),那么速率可表示为:



1.2 基于梳状结构的光学非接触测量系统
在实际应用中,系统光源发出的光照射到路面上,为了实现暗视场照明,照射光束与该系统光轴的角度一般为30°~60°。该测速装置置于车身,随车一起运动,当汽车在某段时间内以速率v运动了一定的距离,在该段时间内,记录路面变化信息的光线反射进入该测速装置,如图2所示[6-8]。光线经过透镜和梳状结构后到达探测器,对两探测器上接收的信号进行采集和差分,会出现周期波动的信号,通过周期提取算法提取该光强信号的周期数,即可实现速度测量[9]。

Fig.2Non-contact optical velocity measurement systems based on grid structure
由于并非是对地面的直接测量和处理,而是对地面反射的光经过透镜在探测器上所成像进行测量和处理,来间接测量速率,所以需要对地面与探测器成像面的倍率关系进行标定。将地面与像面成像关系的横向转换定义为m(pixel/m),即若地面为a(m)的长度,对应成像系统的像素大小为b(pixel),那么横向转换倍率m(pixel/m)为:

当梳状结构确定后,那么一对栅格间距g(m)就确定了,若时间t(s)内点探测器输出光强信号的周期个数为N,那么运动物体的移动速率v(m/s)可以根据(3)式和(4)式写成:

通过上式,即可求出实际系统中运动物体的速率大小。
2地面纹理与周期优化
由(5)式可知,影响测速精度的物理量包括物像标定中的转换倍率m,输出光强曲线的周期数N,栅格对间距g,以及运动时间t。为了得到更加精确的周期数N,本文中主要对栅格对间距g进行讨论,先从理论上分析栅格间距的选择如何影响输出光强信号的周期性,再对实际路面进行分析验证[10-11],讨论如何选择最佳的栅格间距大小。
2.1 不同栅格间距与输出信号周期性的理论分析
图3中从理论上描述了选择不同的栅格间距大小对输出光强信号周期性的影响,当栅格间距大小g/2相对于特征点大小d来说较小时,输出光强信号的周期性不明显,且容易受外部噪声影响;当栅格间距大小g/2相对于特征点大小d来说较大时,输出光强信号出现了周期性的平坦段,容易引起周期数提取误差;只有当栅格间距大小g/2与特征点大小d相近时,输出光强信号的周期性最接近于正弦曲线,此时对后续的信号处理和周期数的提取非常有利。可见,选择合理的栅格间距大小对于输出光强信号周期的优化来说非常重要。

Fig.3 Different outputs corresponding to different intervals in theory
2.2 不同栅格间距与输出信号周期性的实验分析
实际测量系统中常采用差分探测的方法[12],即使两探测器接收到的输出光强信号的相位相差π,再对两光强信号进行差分,分析差分后的信号,这种方法的优点在于不仅解决了单探测器所带来的光强损失问题,同时也解决了对单探测器接收的信号进行处理时存在基频影响的问题。本文中结合图像处理的方法[13],取某面积的图像区域,用隔列取光强的方法代替梳状结构,用该面积图像区域的移动代替物体的移动,当该区域不断向前移动时,隔列取光强求和,每移动一次记录一次光强值,将得到的两组相位差为π的输出光强信号∑A和∑B,对其进行差分处理后,差分输出光强如下式所示:

其理论上的差分情况如图4所示(其中取样的栅格间距p=g/2),纵坐标为光强(单位为cd),横坐标为移动的次数。

Fig.4 Output curves of differential method 多次改变取样的栅格间距p的大小,观察不同栅格间距对输出光强信号周期性的影响,从而确定最佳列间距大小的选择。
3实验数据分析及优化
3.1 对柏油路面的分析
选择一个长为320mm、宽为290mm的矩形柏油路面区域,其特征点大小以1.1mm左右为主,用型号为COOLPIX S3300的相机进行拍摄,其灰度图如图5a所示,其像素大小为2272×1704,此时,1pixel对应实际距离0.14mm,对其进行差分采样,如图5b所示。
由2.1节中的理论分析可知,只有当取样的栅格间距大小与特征点大小相近时,输出信号的周期性最优,对于此路面,其特征点大小为1.1mm左右,对应像素在6~8(0.84mm~1.12mm)之间,同时选择取样的栅格间距明显小于特征点(2pixel对应实际大小为0.28mm)和取样的栅格间距明显大于特征点(13pixel对应实际大小为1.82mm)的两种情况构成对比,于是,分别选择p为2pixel,6pixel,8pixel,13pixel几种情况进行实验。对某面积区域的图像进行隔列采样,当该面积区域向前移动时,将得到两组变化的输出光强信号,改变取样的栅格间距p(pixel),得到不同的输出光强信号,对其差分后将得到如图6所示的输出信号(括号内为像素对应的实际距离)。
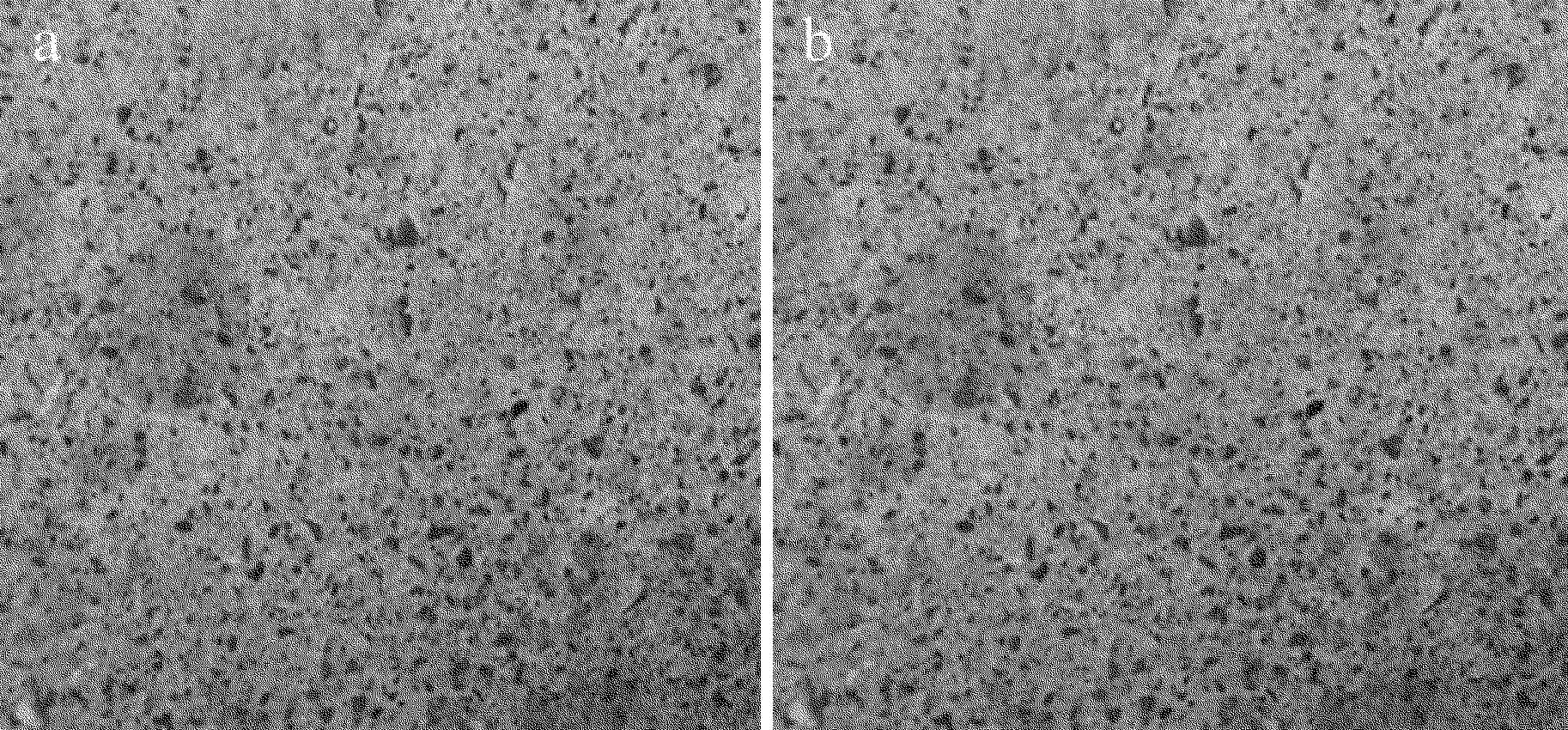
Fig.5 Tarmacadam pavement and its sampling method
由图6可知,当p=8(对应实际路面大小为1.12mm)时,输出光强信号的周期性非常好,p=2pixel(对应实际路面大小为0.28mm)或p=13pixel(对应实际路面大小为1.82mm)时,输出光强信号的周期性较差,若提取该周期数计算速率时,将对速率精度产生较大的影响。
3.2 对水泥路面的分析
选择一个长为590mm,宽为440mm的1个矩形水泥地面区域,其特征点大小以1.5mm为主,用型号为富士f75exr的相机进行拍摄,其灰度图如7a所示,其像素大小为2592×1944。那么,1pixel对应实际距离为0.227mm,对其进行差分采样,如图7b所示。
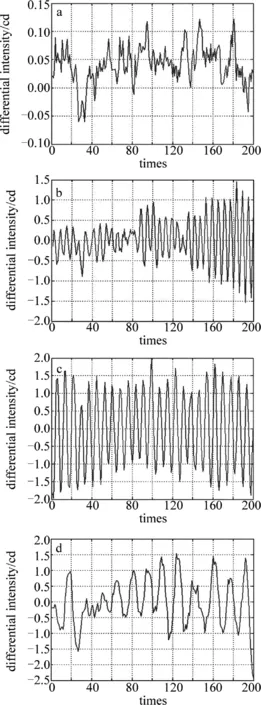
Fig.6Different outputs corresponding to different intervals in experiment
a—p=2pixel(0.28mm)b—p=6pixel(0.84mm)c—p=8pixel(1.12mm)d—p=13pixel(1.82mm)

Fig.7 Cement pavement and its sampling method
该路面的特征点大小为1.5mm左右,对应像素在6~8(1.362mm~1.812mm)之间,同时选择列间距明显小于特征点(2pixel对应实际大小为0.454mm)和取样的栅格间距明显大于特征点(13pixel对应实际大小为1.362mm)的两种情况构成对比,于是,选择p分别为2pixel,6pixel,8pixel和13pixel几组数据进行实验。对某面积区域的图像进行隔列采样,当该面积区域向前移动时,将得到两组变化的输出光强信号,改变p(pixel),得到不同的输出光强信号,对其差分后将得到如图8所示的输出信号(括号内为像素对应的实际距离)。

Fig.8Different outputs corresponding to different intervals in experiment
a—p=2pixel(0.454mm)b—p=6pixel(1.362mm)c—p=8pixel(1.816mm)d—p=13pixel(2.951mm)
由图8可知,当p=6pixel(对应实际路面大小为1.362mm)时,输出光强信号的周期性非常好,当p=2pixel(对应实际路面大小为0.454mm)或p=13pixel(对应实际路面大小为2.951mm)时,输出光强信号的周期性较差,若提取该周期数计算速率时,将对速率精度产生较大的影响。
3.3 实验结果分析
由上述两种路面的实验结果可知,不同的间距大小对输出光强信号的周期性影响很大,对于柏油路面,当取样的栅格间距大小取8pixel(对应的实际长度为1.12mm),此时取样的栅格间距大小与特征点大小相近,对应的输出信号周期性非常理想。对于水泥路面,当取样的栅格间距取6pixel(对应的实际长度为1.362mm)时,此时取样的栅格间距大小与特征点大小相近,对应的输出信号周期性非常理想。综合考虑,在实际系统设计中,为保证良好的输出信号周期性,选择的最佳梳状结构间距范围为1.0mm~1.5mm。值得说明的是,该最佳梳状结构间距大小并非图2所示实际测速系统中梳状结构的间距大小,而是在不考虑透镜系统的转换倍率m时梳状结构的间距大小,只有当再次计算转换倍率m后才能得到实际测速系统中梳状结构的间距大小。
4结论
通过对两种不同的实际路面进行分析可知,不同梳状结构的间距大小对输出光强信号的周期性影响很大,为了提高测速精度,通过讨论最佳的梳状结构间距来实现输出光强信号的周期优化有非常重要的意义。根据理论分析及对柏油路面和水泥路面的分析可知,只有当间距大小与特征大小相近时,输出信号周期性最好,且确定了这两种情况下最佳的梳状结构间距大小为1.0mm~1.5mm;间距选择不能太宽,因为对应的周期个数将较少,不利于提高测速精度;间距不能太小,因为对应的周期数将较多,容易受到环境噪声影响。由于路面情况较为复杂和多样,根据不同的路面特征确定与之一致的栅状结构间距大小,有利于得到最佳的输出信号曲线,方便后续的信号处理。在接下来的工作中,将在实际测速系统中对上述实验结果进行验证,并分析更多有利于实现输出光强信号周期优化的因素。
参考文献
[1]ZHANG Y, CAI C Q, SUN Q. The testing technology of automotive vehicle velocity measurement at home and abroad[J].Chinese Measurement, 2007,33(4):69-70 (in Chinese).
[2]XIE H B, GONG R M, HAN L,etal. Optical system design of a portable laser Doppler velocimeter[J]. Laser Technology, 2011, 35(1): 109-111 (in Chinese).
[3]ZHAO S J, ZHANG P, ZHANG Y Q,etal. Velocity measurement techniques based on laser feedback effect[J]. Laser Technology, 2012, 36(2):160-164 (in Chinese).
[4]ATOR J T. Image-velocity sensing with parallel-slit reticles[J]. Journal of the Optical Society of America, 1963, 53(12):1416-1419.
[5]CHEN Z Z, ZHU X L. Speed measurement photo-electricity sensor and its signal adjustment circuit[J]. Journal of Transducer Technology, 2002, 21(8):53-58 (in Chinese).
[6]AIZU Y, ASAKURA T. Principles and development of spatial filtering velocimetry[J]. Journal of Applied Physics, 1987, B43(4):209-224.
[7]SCHAEPER M, DAMASCHKE N. Velocity measurement for moving surfaces by using spatial filtering technique based on array detectors[C]// Second International Conference, Autonomous and Intelligent Systems 2011. Heidelberg, Berlin, Germany: Springer-Verlag, 2011, 6752: 303-310.
[8]ZHENG L N, ZHANG T, KUANG H P,etal. Image motion velocity measurement technique based on spatial filtering effect of line CCD for aerial camera[J]. Acta Optica Sinica, 2012, 32(11): 1112002(in Chinese).
[9]ZHOU F, ZHAO C Y, HUANG Z Y,etal. Time-domain linear interpolation algorithm and its error analysis for estimating signal period [J].Chinese Journal of Scientific Instrument, 2011, 32(8): 1725-1730 (in Chinese).
[10]USHIZAKA T, ASAKURA T. Measurements of flow velocity in a microscopic region using a transmission grating[J]. Applied Optics, 1983, 22(12):1870-1874.
[11]HAN B, TONG Y, LI J. Flow velocity measurement by spatial filter and experimental research[J]. International Symposium on Modern Measuring Techniques for Multiphase Flows, 1996, 36(12): 356-363.
[12]AIZU Y, USHIZAKA T, ASAKURA T. Measurement of flow velocity in a microscopic region using a transmission grating: a differential type [J]. Applied Optics, 1985, 24(5):627-635.
[13]GONZALEZ R C, WOODS R E. Digital image processing[M].Beijing:Publishing House of Electronics Industry, 2007: 8(in Chinese).
Cycle optimizing method used in optical velocity measurement
systems based on grid structure
LUONa,OUPan,ZHANGChunxi,ZHOUJinnan
(School of Instrumention Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China)
Abstract:In order to improve the measurement precision of optical velocity measurement systems based on grid structure, effect of spacing size of the grid structure on the period of output light intensity signal was studied using mathematical principles. Combined with image processing, optimal spacing size was selected so that the period of the output light intensity signal was optimized and the measurement precision was improved. After relevant theoretical analysis, simulation experiments were carried out for two different kinds of roads. The periodic information of different spacing under different output light intensity was obtained. The results show that when the spacing size of the grid structure is consistent with the surface feature point size, the optimum output light intensity period is obtained. For ordinary asphalt and concrete pavement, the best spacing is 1.0mm~1.5mm corresponding to the ground.
Key words:measurement and metrology; cycle optimizing; image processing; grid structure; differential output
文章编号:1001-3806(2015)01-0076-06
收稿日期:2013-12-12;收到修改稿日期:2014-04-16
作者简介:罗娜(1990-),女,硕士研究生,现主要从事光学测速方面的研究。
基金项目:教育部新世纪优秀人才支持计划资助项目
中图分类号:O348.11
文献标志码:A
doi:10.7510/jgjs.issn.1001-3806.2015.01.014
