基于光子晶体光纤的高斯脉冲光谱压缩数值研究
2015-02-26门艳彬孟义昌张书敏
温 芳,门艳彬,孟义昌,张书敏
(河北师范大学 物理科学与信息工程学院 河北省新型薄膜材料实验室, 石家庄 050024)
基于光子晶体光纤的高斯脉冲光谱压缩数值研究
温芳,门艳彬,孟义昌,张书敏
(河北师范大学 物理科学与信息工程学院 河北省新型薄膜材料实验室, 石家庄 050024)
摘要:为了获得高质量的窄线宽光脉冲,采用单模光纤和光子晶体光纤相结合的光谱压缩技术,通过分步傅里叶变换方法求解非线性薛定谔方程,数值模拟了1550nm波段高斯脉冲光谱压缩过程。结果表明,当初始脉冲的脉宽、峰值功率及所采用光子晶体光纤的参量一定时,光谱压缩存在一最佳光子晶体光纤长度;且初始光脉冲的峰值功率越大,所采用光子晶体光纤的非线性系数越大,所需光子晶体光纤最佳长度越短,所得谱压缩比越大;利用最佳长度为4.152m的光子晶体光纤对峰值功率为110W、初始脉宽为0.65ps的高斯脉冲进行光谱压缩时,可得谱压缩比为3.47的最佳谱压缩光脉冲;脉冲形状对光谱压缩产生一定的影响,高斯脉冲较超高斯脉冲光谱压缩效果更好。该研究结果对研制窄线宽、超短脉冲光纤激光器具有指导意义。
关键词:光纤光学;谱压缩比;自相位调制;高斯脉冲;单模光纤;光子晶体光纤
E-mail:wenfang76@126.com
引言
窄线宽光源可提高光谱分辨率,故在光谱学、非线性显微学、计量学、光纤通信等领域具有广泛应用。锁模激光器所产生的光脉冲脉宽较窄、谱宽较宽。为得到窄线宽光源,人们常采用光谱滤波技术[1],但该方法在滤掉多余波长成分的同时,也降低了光脉冲的能量。而利用光谱压缩技术可获得高亮度、窄线宽光脉冲。1978年,STOLEN等人首次观察到光脉冲在单模光纤传输时自相位调制(self-phase modulation,SPM)对光谱的压缩效应[2]。1993年,OBERTHALER等人进一步理论证明,SPM效应是利用正、负啁啾相互补偿技术使光谱压缩[3]。 尽管利用SPM效应已成功实现了1060nm和800nm波段的光脉冲压缩[4-5]。但为得到负啁啾光脉冲,人们常采用激光谐振腔内插入棱镜对或光栅对技术,该技术操作繁琐,需要精细的光路调节。为了克服这一缺点,研究者提出利用色散渐增光纤(dispersion increasing fiber,DIF)压缩光谱技术。2011年,CHUANG等人实验观察和理论计算了DIF中绝热孤子光谱压缩过程[6-7]。为了获得DIF,在光纤拉制过程中必须时刻监测色散系数的变化,因而获得理想的DIF存在困难。
光子晶体光纤(photonic crystal fiber,PCF)是一种新型光纤,其包层由波长量级的空气孔在2维方向上周期性排列而成。包层的特殊设计使PCF具有宽带单模传输、 高非线性、零色散位置可调等优点[8-9]。若利用PCF对光谱进行压缩,则既可以利用其高的非线性,即利用SPM技术压缩光谱,又可以利用其零色散位置可调的特性,将其与单模光纤相结合,实现色散渐增特性压缩光脉冲,进而实现光谱的高效压缩。作者利用单模光纤与PCF相结合的技术,对光谱进行压缩。研究发现:PCF参量一定时,不同峰值功率和初始脉宽的高斯光脉冲谱压缩比与PCF的长度有关,且存在一最佳光纤长度。初始光脉冲的峰值功率越大、所采用PCF的非线性系数越大,所需PCF最佳长度越短,所得谱压缩比越大。同时,研究还表明:脉冲形状对光谱压缩产生一定影响。对于超高斯脉冲,在峰值功率、PCF参量确定的情况下,最佳光纤长度和谱压缩比与参量m有关,m值越小,最佳光纤长度越短,光谱压缩效果越好。
1理论基础
当脉冲宽度大于0.1ps时,光脉冲在光纤中传输可用下列非线性薛定谔方程描述[10]:
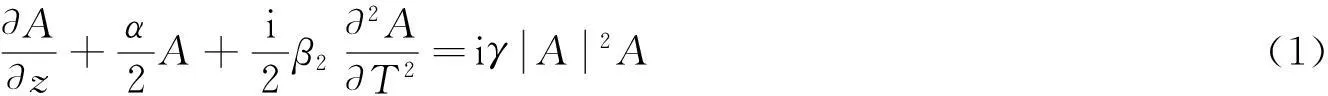
式中,A为脉冲慢变包络振幅,α为光纤损耗系数,β2和γ分别为光纤的群速度色散系数和非线性系数;T是以群速度vg为移动参考系下的时间参量, 即T=t-z/vg,z是脉冲传输距离,t是时间。(1)式等号左边第3项和右边项分别表示光纤的群速度色散(groupvelocitydispersion,GVD)和自相位调制效应。(1)式即为用于描述和计算光脉冲在光纤中传输的理论模型。
当脉冲在光纤中传输时,SPM将引起与脉冲峰值功率P0有关的非线性相移φNL:

式中,L为光纤长度,U为归一化振幅。它与慢变包络振幅A的关系为:

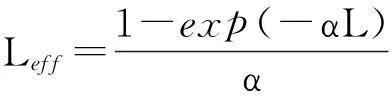
由于φNL的存在,SPM将导致脉冲啁啾效应,使得光脉冲的中心频率与两侧瞬时光频率不同,其差值δω(T)为:

式中,δω(T)称为频率啁啾。对于高斯脉冲,其中心频率附近较大范围内,产生的是线性正啁啾[10]。如果输入的高斯脉冲具有初始负啁啾,而传输时SPM引起正啁啾,两者相互补偿,实现光谱被压缩。
2数值模拟结果与分析

2.1 光脉冲在光子晶体光纤中的演化
选取光子晶体光纤的参量如下[11]:β2=26.8ps2·km-1,γ=70.03W-1·km-1,α=0.2dB·km-1。图1中示出了光脉冲在PCF中的演化过程。由图可见,当脉冲进入PCF后,光谱和脉冲的宽度均发生了变化,且与光纤长度有关。图1a表明,光谱先被压缩,当压缩到一定程度时,随着PCF长度增加,光谱又被展宽,即存在一最佳压缩长度。对此可以这样理解:当脉冲在单模光纤传输时,负色散引起负频率啁啾,使得脉冲前沿频率上移(δω>0),后沿频率下移(δω<0)。而脉冲进入PCF后,自相位调制效应将引起正频率啁啾。两种频率啁啾在高斯脉冲中心附近基本相互抵消,光谱得以压缩。从能量角度看,SPM使脉冲内的能量重新分配到靠近中心波长的成分中,而远离中心波长成分能量变小,光谱变窄[12]。随着光脉冲在PCF中传输,SPM所致的正啁啾逐渐增大,当其超过色散所致负啁啾时,新的频率分量不断产生,将会引起光谱展宽。
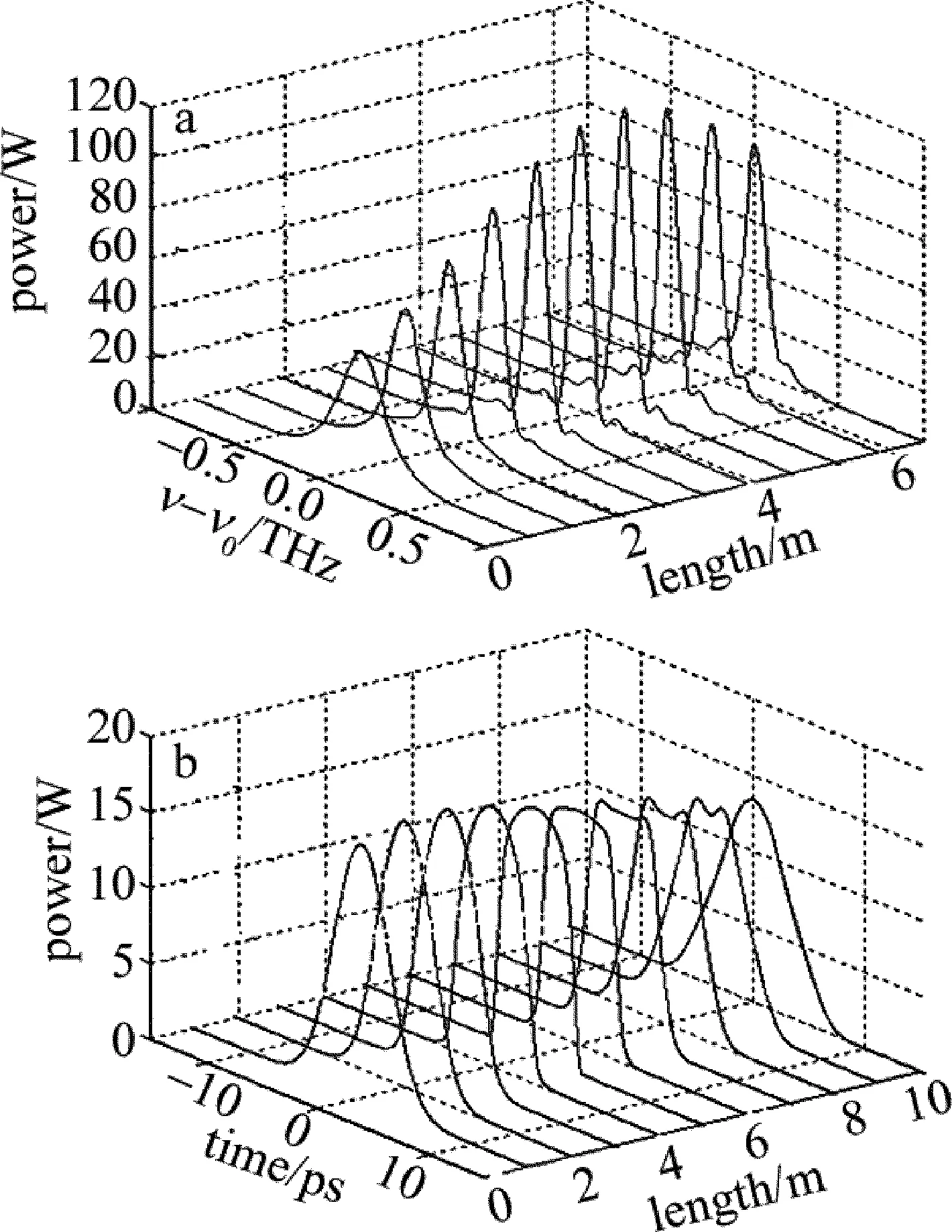
Fig.1 The evolution of the pulse with peak power 90W in PCF
a—spectrum evolution of the pulsesb—temporal evolution of the pulse
2.2 入射脉冲峰值功率对光谱宽度的影响
由(2)式、(3)式可知,自相位调制效应引起的非线性相移与入射高斯脉冲峰值功率P0成正比,故光谱的压缩情况与脉冲峰值功率有关。图2a展示了脉宽、脉冲形状与图1相同、不同峰值功率的光脉冲在上述光子晶体光纤中传输时,所得脉冲光谱宽度随PCF长度变化的关系曲线。该曲线表明,峰值功率确定时,光谱宽度随PCF长度增加先减小而后逐渐增大,将最窄光谱宽度对应的PCF长度,称为最佳光纤长度。图2b则示出在最佳光纤长度时,光脉冲的峰值功率与光谱压缩比的关系曲线。综合两图可见,所有压缩均存在一最佳压缩长度,且峰值功率越大,所需最佳PCF长度越短,所得光谱的压缩比越大。这是因为高峰值功率可产生更强的SPM效应,这样,在较短的PCF处,即可使正、负频率啁啾得到充分补偿,强的SPM效应亦会获得最窄光谱。由图2可知:峰值功率为110W和50W时,最佳PCF长度分别为4.152m和5.856m,谱压缩比为3.47和2.77。

Fig.2a—the relationship between the output spectral width and the input peak powerb—the relationship between the spectral compression ratio and the input pulse peak power
2.3 PCF的非线性系数对光谱宽度的影响
非线性系数是影响自相位调制效应的重要参量,从而也会影响光谱压缩效应。光子晶体光纤的非线性系数可以通过改变包层结构参量灵活设计。尽管包层结构参量亦会影响PCF的色散,但理论上只要设计恰当,色散变化会很小或几乎不变[13]。图3a、图3c和图3d展示了保持PCF的色散(β2=26.8ps2·km-1)和脉冲的峰值功率(110W)不变,非线性系数不同的PCF所产生的压缩光脉冲光谱。由图可见,非线性系数越大,最佳光纤长度越短(见图3a),所得到的压缩后的光谱(ν-ν0)越窄(见图3c),压缩比较大(见图3d)。非线性系数为70.03W-1·km-1,33.80W-1·km-1时,最佳光纤长度分别为4.152m和5.736m(见图3a),谱压缩比分别为3.47和2.56(见图3d)。
实际情况下,PCF的非线性系数变化时,2阶色散也会变化。如果2阶色散为正值,且逐渐增大,数值模拟发现:同一非线性系数,色散越大,最佳光纤长度越短,如图3b所示。对此的解释是:光脉冲在单模光纤中传输时获得负啁啾,成为具有初始负啁啾的脉冲。当它进入具有正常色散的PCF传输,群速度色散致啁啾与初始啁啾是反号的,即GVD使脉冲产生了正啁啾。GVD致正啁啾和SPM致正啁啾叠加,相当于加强了SPM效应,因此,最佳光纤长度变短。
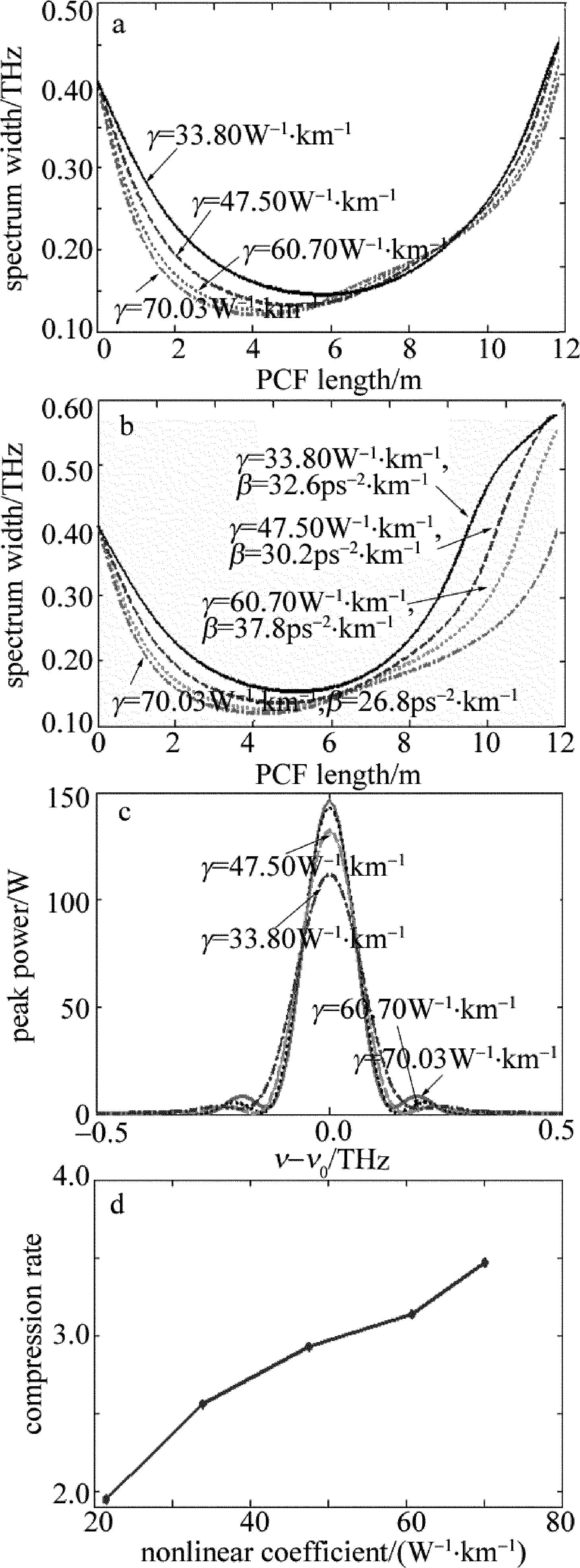
Fig.3a—the relationship between the spectral width and the nonlinear coefficient of PCF whenβ2is constantb—the relationship between the spectral width and the nonlinear and dispersion coefficient of PCF whenβ2is increasingc—the compression figure of the spectrumd—the relationship between the spectral compression ratio and the nonlinear coefficient of PCF
2.4 入射脉冲宽度对光谱宽度的影响
入射脉冲为高斯脉冲形状时,SPM所致的频率啁啾δω(T)为[10]:

由(5)式可知,光谱的压缩情况与高斯脉冲的初始宽度有关。图4中示出脉冲峰值功率为90W、脉宽不同的无啁啾高斯光脉冲在上面所述的PCF中传输时光谱压缩情况。图4b和图4d表明:随着初始脉宽增宽,所需最佳PCF长度逐渐减小,所得谱压缩比逐渐减小。当初始脉宽为0.75ps时,所需最佳PCF长度最短,且仅为2.808m,对应谱宽为0.1223THz的最窄压缩光谱,谱压缩比为2.94。图4a和图4c显示出压缩前、后光谱形状都是高斯型的,SPM没有导致光谱振荡结构的出现。
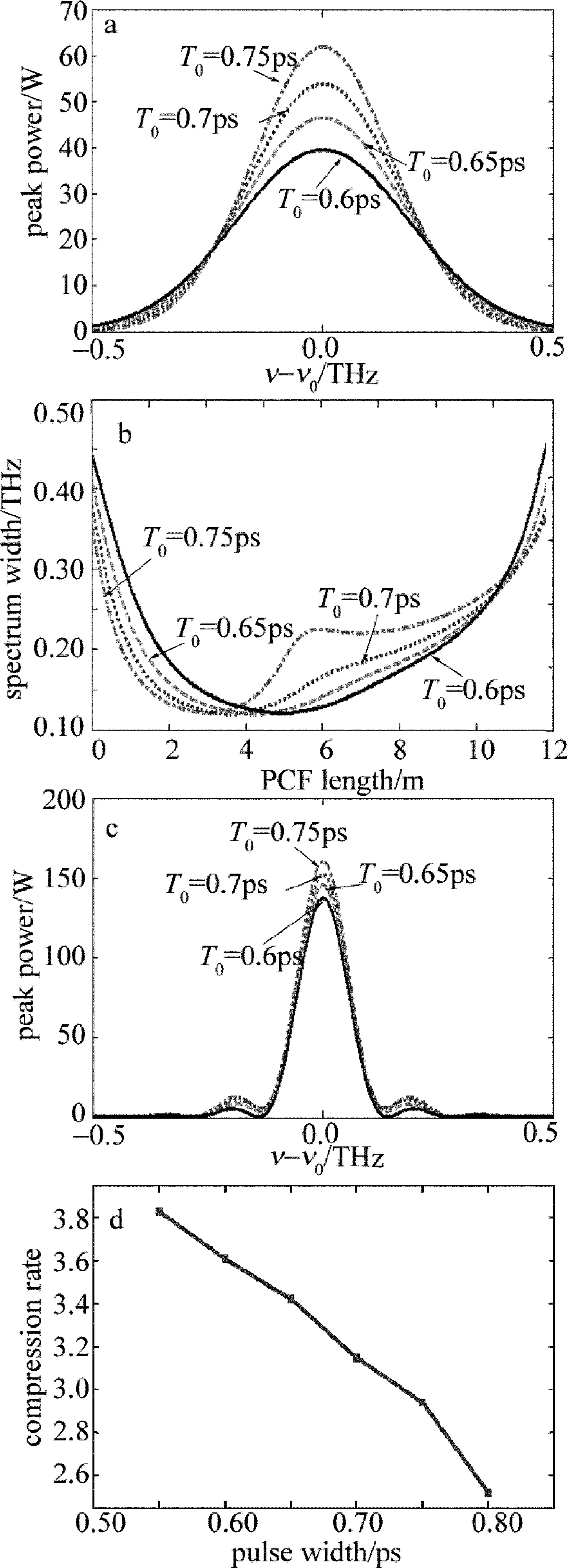
Fig.4a—theinitialspectrumoftheinputpulseb—therelationshipbetweentheoutputspectralwidthandthepulsewidthc—thecompressionspectrumoftheoutputpulsed—therelationshipbetweenthespectralcompressionratioandthethepulsewidth
2.5 入射脉冲形状对光谱宽度的影响

由(6)式可知,光谱的压缩情况与参量m有关,即光脉冲频谱压缩和展宽的程度与脉冲的形状有关。作者选取m为2,3,4和5,讨论不同形状的超高斯脉冲在光子晶体光纤中的光谱压缩情况。
图5a示出,峰值功率为90W、m=3的超高斯脉冲在参量与上面相同的PCF中传输时光谱的演化过程。由图可知:与高斯脉冲相同,超高斯脉冲光谱先被压缩,而后又被展宽,存在一最佳压缩长度。
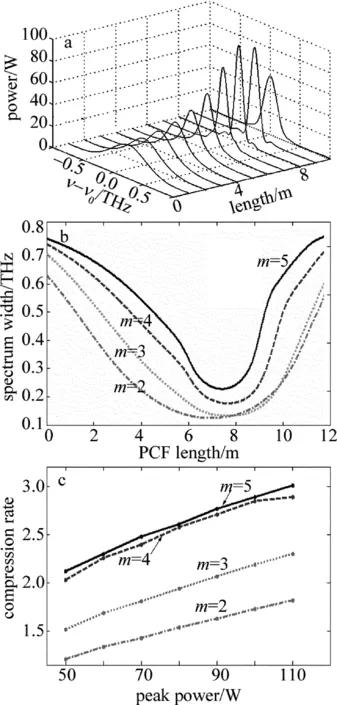
Fig.5a—spectrum evolution of the super Gussian pulse in the PCFs when the peak power of pulse is 90Wb—the relationship between the output spectral width and the parametermc—the relationship between the spectral compression ratio and the input pulse peak power when the parametermis different
图5b示出,峰值功率均为110W,不同参量m的光脉冲在上述PCF中传输时,光谱宽度随长度变化的关系曲线。作者发现,随着参量m增大,最佳光纤长度也增大,而且超高斯脉冲的最佳光纤长度大于高斯脉冲。m=2的超高斯脉冲对应的最佳光纤长度为6.888m,而相同情况下,高斯脉冲为4.152m。由图5c可知:随着峰值功率增加,不同m的超高斯脉冲光谱压缩比均呈现线性增大趋势;相同峰值功率下,参量m越小,谱压缩比越大。峰值功率为110W时,m=2和m=5时的谱压缩比分别为3.01和1.82,而在此条件下,高斯脉冲的谱压缩比为3.47。超高斯脉冲的谱压缩比较小的主要原因是:高斯脉冲中心频率附近较大范围内,产生线性正啁啾,而超高斯脉冲中心频率附近啁啾几乎为0,其频率啁啾主要出现在前后沿附近,且不是线性变化的。因此,SPM致超高斯脉冲的啁啾不能完全抵消单模光纤中产生的频率啁啾,谱压缩比较小。通过以上分析可知:利用PCF压缩光谱,高斯脉冲的压缩效果比超高斯脉冲好。
3结论
讨论了中心波长为1550nm的高斯脉冲在经过单模光纤实现预啁啾后在光子晶体光纤中传输时所产生的光谱压缩过程。结果表明:当所采用PCF的参量一定时,不同的初始脉冲的脉宽、峰值功率存在着最佳光纤长度。且初始光脉冲的峰值功率越大、脉宽越窄、所采用PCF的非线性系数越大,所得谱压缩比越大。与高斯脉冲相比,在相同的条件下,超高斯脉冲对应的最佳光纤长度较长,所获得的光谱压缩比较小。通过合理设计PCF结构,提高非线性系数,改变零色散波长,可以满足不同波长脉冲在PCF中进行高质量的光谱压缩。
参考文献
[1]SZIPOCS R, KOHAZI-KIS A, APAI P,etal. Spectral filtering of femtosecond laser pulses by interference filters[J]. Applied Physics, 2000,B70(s1):S63-S66.
[2]STOLEN R H, LIN Ch L. Self-phase-modulation in silica optical fibers[J]. Physics Review, 1978, A17(4):1448-1453.
[3]OBERTHALER M, HOPFEL R A. Special narrowing of ultrashort laser pulses by selfphase modulation in optical fibers[J]. Applied Physics Letters, 1993, 63(8): 1017-1019.
[4]LIMPERT J, GABIER T, LIEM A,etal. SPM-induced spectral compression of picosecond pulses in a single-mode Yb-doped fiber amplifier[J]. Applied Physics, 2002,B74(2):191-195.
[5]ANDRESEN E R, THOGERSEN J, KEIDING S R. Spectral compression compression of femtosecond pulses in photonic crystal fibers[J]. Optics Letters, 2005, 30(15): 2025-2027.
[6]ChUANG H P, HUANG Ch B. Wavelength tunable spectral compression in a dispersion-increasing fiber[J]. Optics Letters, 2011, 36(15): 2848-2850.
[7]LIANG R, ZHOU X J, ZHANG Zh Y. Spectral compression of femtosecond soliton in a dispersion-increasing fiber[J]. Acta Photonica Sinica , 2010, 39(5): 811-814 (in Chinese).
[8]RUSSELL P S J. Photonic-crystal fibers[J] .Journal of Lightwave Technology, 2006, 24(12):4729-4749.
[9]JIAN D, LIU M, HE D D,etal. Reseach of photonic crystal fiber with high nonlinear flattened dispersion property[J]. Laser Technology, 2013, 37(2):187-190 (in Chinese).
[10]AGRAWAL G P. Nonlinear fiber optics[M].3rd ed. Beijing: Electronics Industry Press, 2002: 64-66(in Chinese).
[11]WU M, LIU H R, HUANG D X. Dispersion property in highly nonlinear photonic crystal fiber[J]. Acta Optica Sinica, 2008, 28(3): 539-542(in Chinese).
[12]WASHBURN B R, BUCK J A, RALPH S E. Transform-limited spectral compression due self-phase modulation in fibers[J]. Optics Letters, 2000, 25(7): 445-447.
[13]SONG D J, XIE K, XIAO J. Mode field and dispersion analysis of photonic crystal fibers based on finite element method[J]. Laser Technology, 2012, 36(1):111-113 (in Chinese) .
Study on spectral compression of Gaussian pulse in photonic crystal fibers
WENFang,MENYanbin,MENGYichang,ZHANGShumin
(Advanced Thin Films Laboratory of Hebei Province, College of Physics Science and Information Engineering, Hebei Normal University, Shijiazhuang 050024, China)
Abstract:In order to get high quality pulse with narrow linewidth, spectral compression of Gaussian pulse was investigated numerically by solving the nonlinear Schrödinger equation. It was found that, when the Gaussian pulse with the central wavelength of 1550nm successively propagated in a single-mode fiber and a photonic crystal fiber, its spectra would be compressed. Further more, when input peak power, pulse width of Gaussian pulse, and nonlinear coefficient of photonic crystal fibers were fixed, there would exist an optimal photonic crystal fiber length. If peak power of the initial light pulse was the greater, nonlinear coefficients of photonic crystal fiber was the larger, the optimal length of photonic crystal fiber was the shorter, the compression ratio of spectra was the greater. The highest spectral compression ratio of 3.47 was achieved for the Gaussian pulse with the input peak power of 110W and the initial pulse width of 0.65ps, while the optimum length of photonic crystal fibers was only 4.152m. The spectral compression of Gaussian pulse was better than super Gaussian pulse under the same simulation condition because of the pulse shape. The results would provide a significant guidance for making the ultrashort pulse fiber laser with narrow linewidth.
Key words:fiber optics;spectral compression ratio;self-phase modulation;Gaussian pulse;single-mode fiber;photonic crystal fiber
文章编号:1001-3806(2015)01-0071-05
收稿日期:2014-01-07;收到修改稿日期:2014-03-11
作者简介:温芳(1976-),女,硕士,讲师,主要研究方向为非线性光纤光学及光纤通讯。
基金项目:国家自然科学基金资助项目(11074065;11374089;61308016);教育部博士点博导类基金资助项目(20101303110003);河北省自然科学基金资助项目(F2012205076;A2012205023);河北省教育厅重点基金资助项目(ZH2011107;ZD20131014);河北师范大学青年基金资助项目(L2011Q05)
中图分类号:TN252
文献标志码:A
doi:10.7510/jgjs.issn.1001-3806.2015.01.013
