shearlet变换和区域特性相结合的图像融合
2015-02-26郑伟,孙雪青,李哲
shearlet变换和区域特性相结合的图像融合
郑伟1,2,孙雪青1,2,李哲1,2
(1.河北大学 电子信息工程学院,保定 071002; 2.河北大学 河北省数字医疗工程重点实验室,保定 071002)
摘要:为了提高多模医学图像或多聚焦图像的融合性能,结合shearlet变换能够捕捉图像细节信息的性质,提出了一种基于shearlet变换的图像融合算法。首先,用shearlet变换将已精确配准的两幅原始图像分解,得到低频子带系数和不同尺度不同方向的高频子带系数。低频子带系数使用改进的加权融合算法,用平均梯度来计算加权参量,以此来改善融合图像轮廓模糊度高的问题,高频子带系数采用区域方差和区域能量相结合的融合规则,以得到丰富的细节信息。最后,进行shearlet逆变换得到融合图像。结果表明,此算法在主观视觉效果和客观评价指标上优于其它融合算法。
关键词:图像处理;图像融合;shearlet变换;加权融合;区域方差;区域能量
E-mail:weizheng799@yahoo.com
引言
图像融合是将两幅或两幅以上的图像合成一幅新图像的过程,但这并不意味着仅仅是把多幅图像相加,而是要使用特定的规则把每幅图像的有用信息综合起来,以获取一幅更加准确、更加全面的新图像。近年来,图像融合技术得到迅猛发展,在遥感探测、医学图像分析、环境保护、交通监测、军事安全等领域[1-2]都有着重大的应用价值。
图像融合算法在早期是基于空域的,直接对源图像的像素灰度空间操作,实现简单但效果欠佳。1983年BURT等人首先提出了金字塔变换,开启了多尺度分解的先河,随着技术的日益发展,小波变换、contourlet变换、非下采样contourlet变换(non-subsampled contourlet transform,NSCT)等相继被提出[3-5]。shearlet变换是LABATE等人[6-7]在2005年时提出来的,克服了小波变换在方向数上的限制,继承了curvelet变换的优良特性,能够对图像进行稀疏表示,此外还有高度的方向敏感性。目前,具有这些优点的shearlet变换在稀疏表示[7]、人脸识别[8]、边缘检测[9]、去噪[10]等领域都有研究,在图像融合领域,CAO等人[11]和MIAO等人[12-13]都证明其融合结果比其它多尺度分解方法包含更多的图像细节信息和边缘轮廓特征。
一个好的融合算法不仅需要好的变换方法,其融合规则的选择也是一个重要问题。低频系数决定着图像的整体特征,以往文献中针对低频系数的融合规则,大多采用加权平均法[11-13],虽然实现简单,但是图像的部分轮廓信息有可能会丢失;至于在高频系数的选取上,考虑到人类视觉系统对高频系数代表的细节信息比较敏感,而且图像模糊或清晰的特征,不能由某个像素的灰度值来体现,需要局部区域内多个像素点的共同体现,多数文献中采用基于区域的融合规则[12-14]。根据以上分析,本文中提出了一种shearlet变换和区域特性相结合的图像融合方法,低频部分采用改进的加权融合的规则,用平均梯度来计算加权参量,改善融合图像边缘清晰度低的问题,高频部分采用区域方差与区域能量相结合的融合规则。通过对多聚焦图像和医学图像进行仿真实验,结果表明,该融合算法能够较好地保留图像的边缘细节,在主观视觉和客观评价上都优于其它融合算法。
1shearlet变换
LABATE等人将合成小波理论与传统的仿射系统理论相结合,提出了一种新的多尺度几何分析方法,即shearlet变换。通过对一个函数进行伸缩、平移、旋转生成一组基函数,使其和多分辨分析关联起来,能够在不同尺度、不同方向对图像的细节信息进行有效描述。

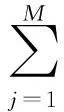

Fig.1 Zoneplate image and the sub-band images
a—zoneplate imageb—low frequency sub-band imagec~f—four sub-band images of the first level decompositiong~l—six sub-band images of the second level decomposition
2融合规则的选取
shearlet变换的融合步骤:首先用shearlet变换将已经配准好的源图像A、B分解,得到分解后的高低频子带系数;然后对高低频子带系数分别采用不同的融合规则,得到融合后的高低频系数;最后进行shearlet逆变换得到融合图像F。
2.1 低频系数的融合规则
由shearlet变换分解得到的低频子带系数,包含了图像的主要信息,决定着图像的整体特征,以往的融合算法一般选用简单的加权平均方法,降低了融合图像的对比度,忽视了低频系数对图像的整体作用。本文中采用改进的加权融合算法,加权规则如下所示:
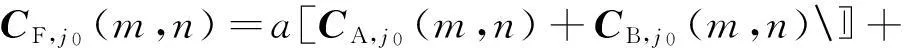




式中,GX,j0为低频系数的平均梯度,X=A,B。
2.2 高频系数的融合规则
高频子带系数包含丰富的细节信息,由于像素之间存在较大的相关性,单个像素无法表达图像的区域特征,不能判断图像清晰与否,需要局部区域内多个像素点的共同体现,因此本文中提出区域特性的融合规则。针对高频系数的特性,区域方差取大法侧重于保留边缘细节丰富的区域,但忽视了两幅图像的相关性;区域能量取大法既体现了图像的相关性又保留了图像的细节信息,但容易忽略亮度较低的细节信息,为此本文中采用区域方差与区域能量相结合的融合规则:






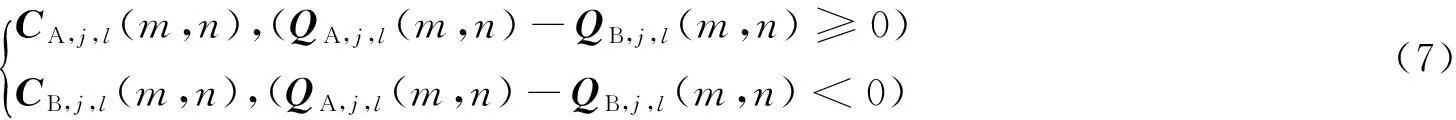
3实验结果及分析
实验环境为MATLAB 7.9,中央处理器为2.10GHz,内存2GB,实验中所用的多聚焦图像为常用的钟表图像和实验室图像,这些图像选自参考文献[11],医学图像为颅脑的计算机断层扫描(computed tomography,CT)、核磁共振(magnetic resonance imaging,MRI)图像和甲状腺肿瘤的B超、单光子发射计算机断层扫描(single-photon emission computed tomography,SPECT)图像,颅脑图像来源于参考文献[13],甲状腺肿瘤图像由河北大学附属医院提供。本文中所用的客观评价指标为:结构相似度(structural similarity,SSIM);标准差(standard deviation,SD);互信息(mutual information,MI);信息熵(information entropy,IE);平均梯度(average grads,AG)[15]。
3.1 变换方法的选取
在图像融合过程中,多尺度分解方法有很多,不同的分解方法对融合结果都会产生一定的影响,所以需要对此进行仿真实验。为了找到合适的变换方法,在融合规则固定的情况下,将本文中提出的shearlet变换与传统的小波变换、contourlet变换以及NSCT作对比。在实验中,将这4种多尺度分解方法的分解层数调成一致,并通过主观视觉和客观评价进行验证。在此分为2组实验,第1组实验是多聚焦图像的仿真实验,如图2所示。
图2a~图2f是多聚焦钟表图像及其融合结果;图2g~图2l是多聚焦实验室图像及其融合结果。图2a和图2g是左聚焦图像,特点为左半边清晰,右半边模糊;图2b和图2h是右聚焦图像,特点为左半边模糊,右半边清晰;图2c和图2i是基于小波变换的融合算法得到的融合图像,从白色矩形区域可以看出,图2c中大钟和小钟的边缘处信息均损失严重,而且小钟图像的时间指示不清晰,图2i中时钟部分有波纹出现,人物头像有明显的虚影存在;图2d和图2j是基于contourlet变换的融合算法得到的融合图像,图2d中小钟刻度模糊,大钟的边缘有重影现象,图2j中人物头像处有重影;图2e和图2k是基于NSCT的融合算法得到的融合图像,两幅图像中的钟表的时间刻度均不清晰;图2f和图2l是基于本文中提出的shearlet变换的融合算法得到的融合结果,能够清晰看到钟表的时间刻度,人物头像不存在重影现象,融合效果自然,更加符合人眼的视觉感受。

Fig.2 Multi-focus source images and the fused images
表1中列出了图2中多聚焦图像融合结果的客观评价指标,可以看出,在源图像为钟表的实验结果中,基于shearlet变换的融合算法只有信息熵,平均梯度的数值小于其它算法,其余指标均高于其它方法;在源图像为实验室的融合结果中,只有平均梯度小于其它算法,其余指标均是最优。这些数据表明,在多聚焦图像融合上,基于shearlet变换的融合算法得到的融合图像能够最大程度继承源图像中的信息,细节信息最为丰富,具有更好的融合性能。
第2组是医学图像的仿真实验,如图3所示。

Table 1 Objective evaluation index of the multi-focus fused images
从图中可以得知,医学图像与多聚焦图像有所不同,即便有的区域模糊,有的区域清晰,但是大部分信息还是相同的,而医学图像由于成像机理不同,所以得到的图像侧重点也不同,除了基本轮廓相似外,几乎没有相同的地方,因此,这类图像融合要更侧重于方法的选取。
图3a~图3f是颅脑的源图像及其融合结果;图3g~图3l是甲状腺肿瘤的源图像及其融合结果。图3a是颅脑的CT图像,体现的是脑部的骨骼信息;图3b是是颅脑的MRI图像,体现的是脑部的软组织信息;图3g是甲状腺肿瘤的B超图像,为解剖成像,可提供脏器组织结构的信息;图3h是甲状腺肿瘤的SPECT图像,为功能成像,可提供肿瘤的良性和恶性信息。所用的变换方法与第1组实验相同,从视觉效果上来看,基于小波变换得到的融合图像亮度偏低,从标记区域处可以看到,颅脑图像边缘出现模糊现象,甲状腺图像中肿瘤模糊不清,不容易区分;基于contourlet变换和基于NSCT得到的融合图像,融合效果均有一定的改善,但边缘处还是有波纹出现,细节信息有损失;本文中提出的基于shearlet变换得到的融合图像从视觉上看,边缘处的细节信息保存较好,清晰度高。
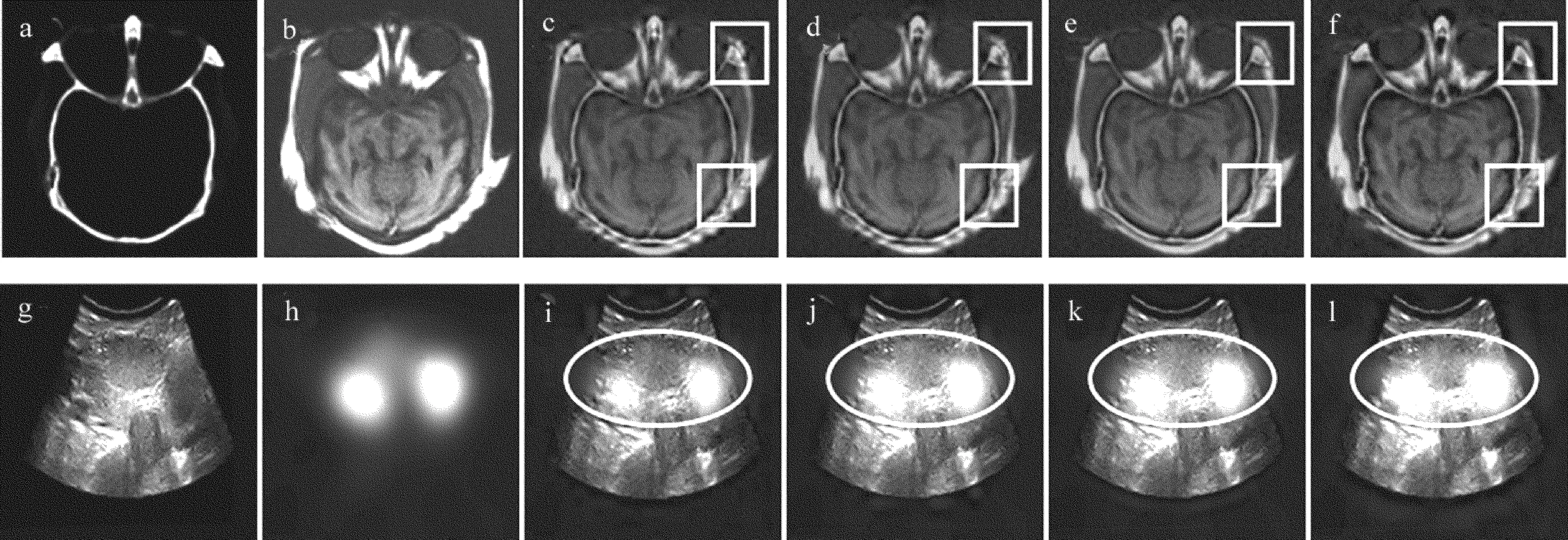
Fig.3 Medical images and the fused images
表2为图3融合结果的客观评价指标,对表2中数据进行分析发现,基于shearlet变换的融合算法在标准差、信息熵、平均梯度上都优于小波变换、contourlet变换和NSCT的融合算法,特别是平均梯度,有明显的提高。这些数据表明,在医学图像融合上,基于shearlet变换的融合算法得到的融合图像有足够丰富的细节信息,清晰度也优于其它变换方法。
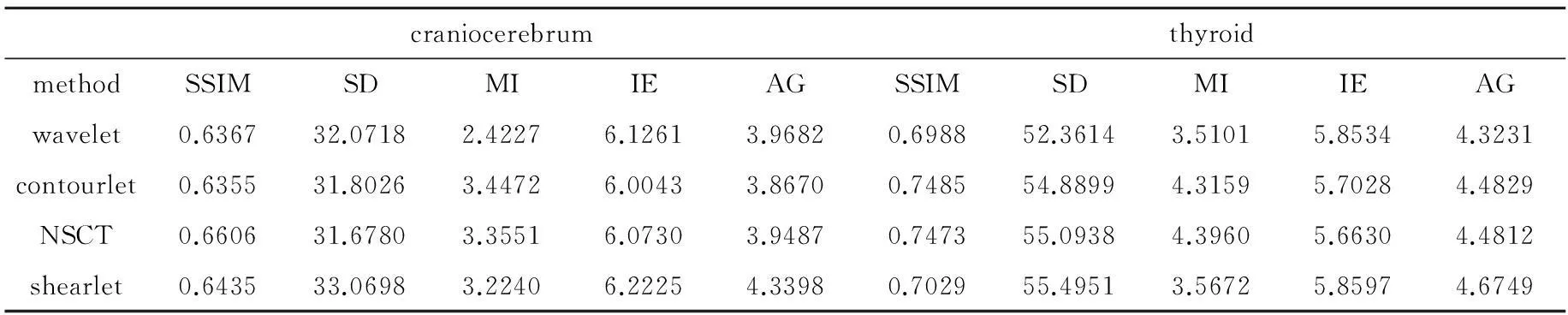
Table 2 Objective evaluation index of the medical fused images
3.2 融合算法的对比
将本文中的算法(简称方法6)与近几年提出5种的融合算法作对比,方法1是参考文献[16]中提出的基于离散余弦变换的图像融合算法,直流系数取平均,交流系数采用对比度取大法,参量按照文献中给定的数据来设置;方法2~方法4分别由参考
文献[11]~参考文献[13]中提出,都是基于shearlet变换的图像融合算法,这3种方法的低频系数均采用传统的加权平均,高频系数分别使用绝对值取大法,区域绝对值取大法,区域方差取大法;方法5为参考文献[14]中提出的基于shaerlet变换的融合算法,低频系数用自适应的融合规则,高频系数使用区域方差取大法。把shearlet变换的分解层数与分解方向数调成一致,区域大小均调整为3×3,实验中选用的图像分别是多聚焦钟表图像和甲状腺肿瘤的B超、SPECT图像,其融合结果如图4所示。

Fig.4 Fused images of different fusion methods
图4a~图4f是多聚焦钟表图像使用不同融合方法得到的融合结果,从视觉效果来看,这6幅图像均保留了源图像的主要信息,亮度适中,符合人眼视觉;图4g~图4l是甲状腺肿瘤图像得到的融合结果,从视觉上来看,图4g比较模糊,有明显的块效应;图4h和图4i亮度偏暗,对比度低,可视性较差,说明方法1至方法3并不适合在医学图像融合中使用;图4j边缘轮廓清晰度偏低,且肿瘤信息有扩散现象,不适合临床诊断使用;图4k的融合效果较好;图4l是本文中算法得到的融合图像,从视觉上看能把甲状腺肿瘤的B超和SPECT图像很好地融合在一起,细节信息保存完好,边缘特征明显,而且亮度适中。
表3为图4中融合结果的客观评价指标,对表中数据进行分析可以发现,在源图像为多聚焦钟表的实验结果中,本文中的算法除了在互信息上不是最优,其余指标值均是最优;在源图像为甲状腺肿瘤的实验结果中,本文中的算法得到的融合图像在结构相似度和互信息上的指标值不是最好的,但其余指标值均是最优,而且都有明显的提高。这是由基于区域特性的融合规则所造成的,因为两个局部区域值相差不大时,会直接选择区域值较大的系数,因此会造成部分有用信息的丢失,产生失真现象。多聚焦图像即使聚焦区域不同,但其背景信息相同,因此损失的信息较小,而医学图像相差较大,一旦有信息损失,就会使源图像的细节特征得不到充分保留,导致融合图像边界模糊,产生失真现象。

Table 3 Objective evaluation index of different fusion methods
4结论
提出了一种shearlet变换和区域特性相结合的图像融合方法,分别对多聚焦图像和医学图像进行仿真实验。在变换方法的对比中发现,基于shearlet变换的融合算法在主观视觉和客观评价上都要优于小波变换、contourlet变换以及NSCT的融合算法。在融合规则的对比中发现,本文中的融合算法与文献中提出的算法在多聚焦图像融合中均获得了较好的效果;在医学图像融合中,本文中的算法得到的融合图像在视觉效果上要远好于文献中提出的算法,在客观评价上,除了结构相似度和互信息的指标值不是最好的,其余指标值均是最优。总而言之,不论在主观视觉上还是在客观评价上本文中的算法都显示了其强大的优越性。
参考文献
[1]GAO Y, WANG A M, WANG F H,etal. Application of improved wavelet transform algorithm in image fusion[J]. Laser Technology, 2013, 37(5): 690-695(in Chinese).
[2]YU W J, GU G H, YANG W. Fusion algorithm of infrared polarization images based on wavelet transform[J]. Laser Technology, 2013, 37(3): 289-292(in Chinese).
[3]MINH N D, VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation [J]. IEEE Transactions on Image Processing, 2005, 14(12):2091-2106.
[4]ZHANG Q, GUO B L. Multifocus image fusion using the nonsubsampled contourlet transform[J]. Signal Processing, 2009, 89(7): 1334-1346.
[5]JIAO L C, TAN S. Development and prospect of image multiscale geometric analysis [J]. Acta Electronica Sinica, 2003, 31(12A):1975-1981(in Chinese).
[6]EASLEY G R, LABATE D, LIM W Q. Optimally sparse image representations using shearlets[C]// Fortieth Asilomar Conference on Signals, Systems and Computers. New York, USA:IEEE, 2006: 974-978.
[7]EASLEY G R, LABATE D, LIM W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied and Computational Harmonic Analysis, 2008, 25(1):25-46.
[8]BORGI M A, LABATE D, EL’ARBI M,etal. Shearlet network-based sparse coding augmented by facial texture features for face recognition[C]//The 17th International Conference on Image Analysis and Processing. Berlin,Germany:Springer, 2013:611-620.
[9]YI S, LABATE D, EASLEY G R.etal. A shearlet approach to edge analysis and detection[J]. IEEE Transactions on Image Processing, 2009, 18(5): 929-941.
[10]HU H Z, SUN H, DENG C Z. Shearlet shrinkage de-noising based total variation regularization [J]. Journal of Image and Graphics, 2011, 16(2):168- 173(in Chinese).
[11]CAO Y, LI S T, HU J W. Multi-focus image fusion by nonsubsampled shearlet transform[C]// 2011 Sixth International Conference on Image and Graphics (ICIG).New York, USA:IEEE, 2011:17-21.
[12]MIAO Q, SHI C, XU P,etal. Multi-focus image fusion algorithm based on shearlets[J]. Chinese Optics Letters, 2011, 9(4): 041001.
[13]MIAO Q, SHI C, XU P,etal. A novel algorithm of image fusion using shearlets[J]. Optics Communications, 2011, 284(6): 1540-1547.
[14]SHI Z, ZHANG Z, YUE Y G. Adaptive image fusion algorithm based on shearlet transform [J]. Acta Photonica Sinica, 2013, 42(1):115-120(in Chinese).
[15]HONG R C. Research on multi-source image fusion and its applications [D].Hefei:University of Science and Technology of China, 2007: 82-88(in Chinese).
[16]HU L M, ZHANG J, XIE Z,etal. Contrast measure based image fusion algorithm in the DCT domain [J]. Chinese Journal of Scientific Instrument, 2007, 28(s3):105-109(in Chinese).
Image fusion based on shearlet transform and region characteristics
ZHENGWei1,2,SUNXueqing1,2,LIZhe1,2
(1. College of Electronic and Information Engineering, Hebei University, Baoding 071002, China; 2.Key Laboratory of Hebei on Digital Medical Engineering, Hebei University, Baoding 071002, China)
Abstract:In order to improve the performance of multi-modality medical image fusion and multi-focus image fusion, since the shearlet transform can capture the detail information of images, an image fusion algorithm based on shearlet transform was proposed. Firstly, the shearlet transform was used to decompose the two registered original images, thus the low frequency sub-band coefficients and high frequency sub-band coefficients of different scales and directions were obtained. The fusion principle of low frequency sub-band coefficients was based on the method of weighted fusion, using the average gradient to calculate the weighted parameters in order to improve the edge fuzzy of the fused image. As for the high frequency sub-band coefficients, a fusion rule adopting the region variance combining with the region energy to get the detail information was presented. Finally, the fused image was reconstructed by inverse shearlet transform. The results show that the algorithm is superior to other fusion algorithms on subjective visual effect and objective evaluation.
Key words:image processing;image fusion;shearlet transform;weighted fusion;region variance;region energy
收稿日期:2014-01-14;收到修改稿日期:2014-02-28
作者简介:郑伟(1972-),女,博士,现主要从事图像处理、图像安全通信的研究。
基金项目:河北省教育厅高等学校科学研究计划资助项目(2010218);河北大学医工交叉研究中心开放基金资助项目(BM201103)
中图分类号:TP391
文献标志码:A
doi:10.7510/jgjs.issn.1001-3806.2015.01.010
文章编号:1001-3806(2015)01-00050-07
