大跨度结合梁斜拉桥减振研究

刘　超　杨名超　周柏宇　刘前瑞

(中国市政工程中南设计研究总院有限公司　上海　200120)

大跨度结合梁斜拉桥减振研究

刘超杨名超周柏宇刘前瑞

(中国市政工程中南设计研究总院有限公司上海200120)

摘要以大跨度结合梁斜拉桥海南洋浦大桥为研究对象。运用Midas/civil2010建立考虑桩-土效应的空间有限元模型，采用动态时程分析法研究该桥在地震荷载作用下的地震响应。分析研究粘滞阻尼器不同参数组合的减振效果，得出一组最佳的参数组合，探讨粘滞阻尼器对结构自振特性和抗振性能的影响。

关键词混合梁斜拉桥地震响应桩-土-结构相互作用粘滞阻尼器

结合梁斜拉桥因其优良的结构特点，在工程实际中运用广泛。这类桥型的主跨跨度大，结构柔性大，发生地震破坏的后果十分严重，故其在地震作用下的动力响应和减振措施值得深入研究。随着科学技术的进步，出现了很多类型的减振装置，粘滞阻尼器作为其中的一种减振装置，通过增加结构的阻尼来吸收地震、风荷载等其他因素引起的破坏能量，可以有效地耗散破坏能量，减少这些外界因素引起的振动。在工程实践中，粘滞阻尼器越来越多地运用到桥梁的抗振中，阻尼器的参数选择在很大程度上也决定了桥梁的抗振性能。

1粘滞阻尼器减振原理

粘滞阻尼器是一种运用较为广泛的耗能减振装置，其减振原理是:当活塞与缸筒之间发生相对运动时，活塞前后的压力差会迫使流体阻尼材料从阻尼器中的阻尼孔通过，进而产生阻尼力，达到耗能减振的目的[1]。

粘滞阻尼器在有限元软件中采用力学模型来进行模拟。常用的力学模型有如下几种：线性模型、Kelvin模型、Maxwell模型、Wiechert模型，以及基于分数微分形式的模型[2]。

粘滞阻尼器的力学性能表达式

(1)

式中：ξ为阻尼指数；v为相对运动速度；F为阻尼力；C为阻尼系数。

当ξ<1时，为非线性粘滞阻尼器；当ξ>1时为超线性阻尼器；当ξ=l时阻尼器成为线性阻尼器。粘滞阻尼器的耗能减振效果是由阻尼系数C和阻尼指数ξ决定的，合理地选取C和ξ才能达到最佳的减振效果，保证结构在地震荷载作用下的动力响应最理想。

本文选用实际工程中运用最多的Maxwell模型来模拟粘滞阻尼器，Maxwell模型中阻尼器与弹簧串联，见图1。

图1　Maxwell模型

假设阻尼器与“弹簧”的位移分别为u1(t)和u2(t)，则有下述关系成立。

(2)

(3)

则由上式可推导得：

(4)

式中：C0为零频率时的线性阻尼常数；Fd(t)为阻尼器抗力；K为刚度系数；λ=C0/K为放松时间常数。

式(4)也可表达为

(5)

2计算模型的建立

2.1　工程概况

本文选取的实例工程为海南洋浦大桥的主桥，主塔形式呈H钻石形，塔高149.5 m。主桥采用(58.5 m+63 m+58.5 m)+460 m+(58.5 m+63 m+58.5 m)=820 m的双塔双索面混合式结合梁斜拉桥。跨中设置440 m工字钢结合梁段，两侧边跨各190 m混凝土边主梁，桥面全宽31.4 m。边跨设置2个边墩，2边各2个辅助墩。中跨部分为钢梁上铺设桥面板形式。

2.2　有限元空间模型的建立

使用MIDAS/CIVIL2010来进行建模和计算分析，采用单主梁模式，主梁和墩塔用梁单元模拟，斜拉索用桁架单元模拟，并用土弹簧来模拟桩土效应[3]，建立了考虑桩土效应的全桥模型，见图2。全桥共7 409个节点，7 399个单元，其中梁单元7 255个，桁架单元144个。

图2　全桥有限元模型

边界条件的模拟：斜拉索与主梁节点刚性连接；主梁与桥墩、主梁与主塔采用弹性连接来模拟；辅助墩和主塔下横梁处设置竖向承载的多向活动球形抗振支座；在支座处设置横向挡块来限制桥梁结构在横桥向的位移，在本文中，将其假设为横向约束条件；中跨桥面板与钢梁刚性连接在一起。主梁类似于多点弹性支承的连续梁，结构实际上为半漂浮体系。斜拉索的成桥索力采用未知系数法进行试算得出。不考虑其他的临时荷载、施工荷载、临时支承以及施工过程边界条件的影响。

3减振器的布置

粘滞阻尼器一般布置在主塔处[4-5]，本桥的阻尼器布置方案为：在塔梁间设置纵向阻尼器，即在主梁与桥塔横梁处设置阻尼器(2组共4个)。

4地震响应分析

4.1　地震波的输入

根据海南省海洋地震与工程地震研究中心海南洋浦——白马井海湾跨海大桥工程场地地震安全性评价报告》，设计采用地震参数见表1。

表1　地表水平峰值加速度与地震系数K值

桥址场地为II类场地，这里选用的是适合这类场地的69°方向Taft地震波。在Midas/Civil 2010中，提供的地震波Taft的最大水平加速度值为0.155 7g(1952, Taft Lincoln School, 69°顶点-0.155 7g持续时间54.38 s),所以需要将其做修正，以满足规范要求。本桥按照8级地震进行设防。《建筑抗震设计规范》(GB 50011-2001)中对地震的持续时间做出了规定，一般取为自振周期的5~10倍[6]。这里选用Taft波是满足要求的。本文采用的地震荷载工况为纵向+竖向，取竖向地震荷载为水平向的67%，没有对横向地震荷载作用进行研究。这里选择地震动时间为50 s，计算时间步长取为0.1 s。水平加速度时程曲线见图3。

图3　水平加速度时程曲线

4.2　阻尼器参数的选择

选取几组不同参数来模拟阻尼器，并对计算模型进行相应的修改。参数组合见表2。

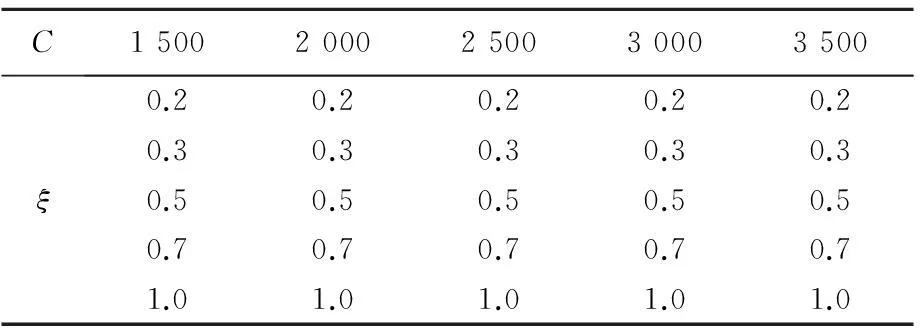
表2　阻尼参数组合

采用时程分析法对每种参数组合的全桥模型进行地震反应分析，得出阻尼指数和阻尼系数对结构抗振效果的影响。见图4～7。

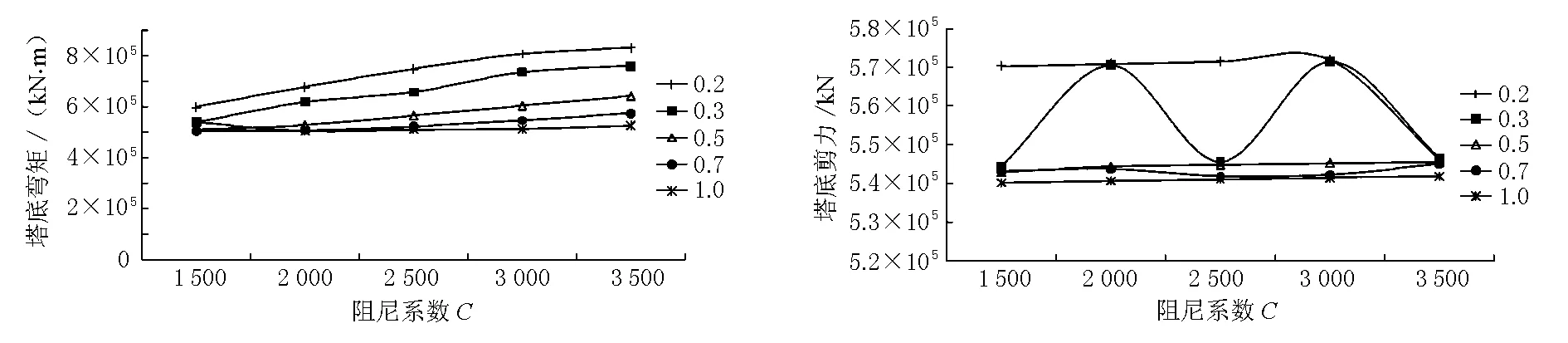
图4塔底弯矩变化曲线图5塔底剪力变化曲线

图6塔顶位移DX变化曲线图7梁端位移DX变化曲线

结合上述的计算结果分析可知，塔底内力与塔顶位移的变化规律是相反的，要想减少塔底的内力，则需要增大阻尼指数ξ，减小阻尼系数C；而要减小塔顶的位移ξ，则需减小阻尼指数，增大阻尼系数C。由此可见，这两者不能同时满足，是相互矛盾的。减小塔底内力，则会增大塔顶位移；相反，减小塔顶位移则会增大塔底内力。

本文中为了选取合理恰当的阻尼指数ξ和阻尼系数C，在综合考虑内力和位移2个因素的前提下，选取ξ=0.7，C=2 000。此时，塔底弯矩为5.08×105kN·m，顶位移DX=0.215 m。

4.3　自振特性与减振效果分析

经过上述计算，得到最佳的参数组合为ξ=0.7，C=2 000。将此参数作为阻尼器的最终参数，对计算模型中的阻尼器参数进行修改。通过计算得到有阻尼器和无阻尼器2种模型的自振特性。这里只选取前10阶振型，见表3。

表3　阻尼体系自振特性

由表3可见，比较2种模型的自振特性发现：前10阶振型的振型特点是一致的，而无阻尼器模型的第一阶振型(主梁纵飘)的自振频率更小。这说明粘滞阻尼器能够很好地增加结构在纵桥向的整体刚度，起到限制结构纵向位移的作用。阻尼装置的设置是成功和必要的。阻尼体系的减振效果见表4，表5。

表4　主要控制截面内力响应

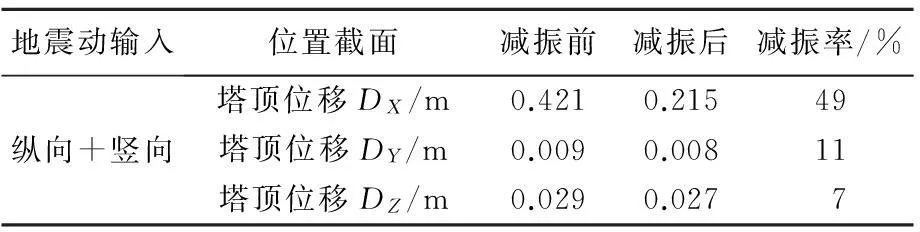
表5　主要控制节点位移响应

5结语

本文采用MIDAS/CIVIL2010建立结构的空间有限元模型，采用动态时程分析法进行地震响应分析，选用粘滞阻尼器进行减振设计，选取最佳的阻尼器参数组合。通过上述研究工作，得出以下结论：

大跨度结合梁斜拉桥，具有柔度大、自振周期大、自振频率低、结构模态密集等特点。粘滞阻尼器能够很好地改善结构在地震荷载作用下的受力特点，当发生地震时能够很好地起到耗散地震能量的作用。设置粘滞阻尼器之后，结构的地震响应在位移和内力两方面都有显著的下降。合理的选择阻尼器参数能够起到更好的减振效果, 本文通过计算分析得出：当取ξ=0.7，C=2 000时，塔顶位移下降49%，塔底弯矩下降30%。

参考文献

[1]朱浩,粘滞阻尼器在斜拉桥减振设计中的应用[D]. 北京：北方交通大学，1999.

[2]宋智斌.粘滞消能减振技术在结构抗振加固中的研究和应用[D].北京:中国建筑科学研究院,2001.

[3]张庆.吴江学院路斜拉桥抗振分析[J].交通科技，2010(10):16-18.

[4]叶正强,李爱群,程文攘,等.采用粘滞流体阻尼器的工程结构减振设计研究[J].建筑结构学报，2001,22(4):61-66.

[5]姜涛，张哲，邱文亮.一座自锚式悬索桥的减振设计[J].武汉理工大学：交通科学与工程版，2014(2)：371-374.

[6]GB 50011-2001建筑抗振设计规范[S].北京：中国建筑工业出版社，2002.

收稿日期：2015-01-13

DOI 10.3963/j.issn.1671-7570.2015.03.002