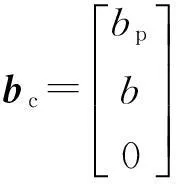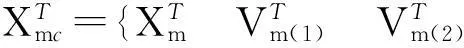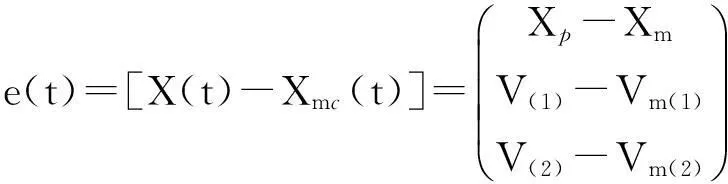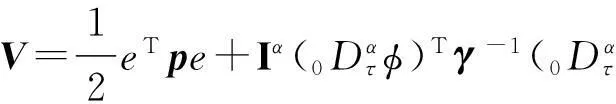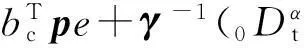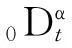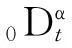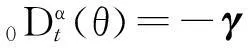应用Lyapunov理论设计分数阶模型参考自适应控制律

白珍龙，刘川来

(1． 中海油山东化学工程有限责任公司，济南 250101；

2． 青岛科技大学 自动化学院，山东 青岛 266042)



应用Lyapunov理论设计分数阶模型参考自适应控制律

白珍龙1，刘川来2

(1． 中海油山东化学工程有限责任公司，济南 250101；

2． 青岛科技大学 自动化学院，山东 青岛 266042)

稿件收到日期： 2015-03-18，修改稿收到日期： 2015-07-04。

德国数学家帕克斯在1966年提出了采用Lyapunov第二法推导模型参考自适应系统(MRAS)的自适应控制律，以保证系统具有全局渐近稳定性，MRAS设计从而进入了采用稳定性理论设计准则的阶段，同时给自适应控制技术带来了生机，使其得以迅速发展和使用。目前，Lyapunov第二法已经得到了广泛应用，并在实际工程中形成了许多成熟的典型方案。

控制论是基于整数阶微积分发展起来的。分数阶微积分不像整数阶微积分那样具有明确的物理意义和几何解释，使得对于分数阶微积分概念的理解比较困难。尽管现存的系统都是分数阶的，但是由于分数阶本身的复杂性，且目前所接触到的系统大多已经取得了较好的整数阶辨识，因而现在对于分数阶的研究主要集中在分数阶控制器的设计和实现上。

1整数阶模型参考自适应控制

自适应控制系统能够辨识外界环境条件或系统本身变化， 自动修正控制系统参数或控制作用， 使系统达到预期状态。模型参考自适应以其简单的结构、优良的控制效果成为自适应控制中比较流行的一种控制方法。

MARS通过在基本调节回路中，用调节器参数的匹配使系统得到一个事先确定的模型特性，它可以处理缓慢变化的不确定性对象的控制问题。其基本控制思想是： 利用可调系统的各种信息，度量或测出某种性能指标，把它与参考模型的性能指标相比较，然后用所得的偏差(广义误差)通过自适应机构产生自适应控制律来调节系统，以削弱可调系统因“不确定性”所造成的性能指标偏差，当可调系统的特性与期望的参考模型特性逐渐一致时，广义误差e趋于极小值或者下降为零，调节过程结束，达到使被控对象获得较好的性能指标的目的。因此，MARS的工作过程可以看作期望的参考模型与实际系统响应之间误差的调整过程。模型参考自适应控制原理如图1所示。

图1　模型参考自适应控制原理示意注： r ——输入；u——控制信号

由于目前实际应用的多数对象已采用传统方式取得了整数阶辨识模型，所以笔者仍将分数阶控制器用于整数阶模型对象，即把系统的未知参数的辨识模型看作是分数阶的，设计了一个简单分数阶自适应控制律，期望得到优于传统方法性能的控制律。其主要优势在于采用简单的分数阶控制器即可取得比整数阶控制器更优的动态性能和鲁棒性。

2分数阶模型参考自适应控制律的设计

2．1设计步骤

按照Lyapunov稳定性理论设计MARS的步骤如下：

1) 根据系统的工作原理列出系统的数学模型，主要包括被控对象的数学模型、参考模型的数学模型和控制器的数学模型。

2) 建立等效的误差系统。当系统各个部分的数学模型列出后，系统的设计问题就相应地转化为对等效误差系统稳定性的研究。

3) 根据系统的稳定性要求，为系统选择一个合适的Lyapunov函数。通常该函数包括两部分： 系统状态(或输出)的二次型函数；系统的可调整控制器参数的二次型函数。

4) 对Lyapunov函数求其对时间的k (0

2．2用系统的输入输出设计分数阶的控制器

通常利用系统的状态方程设计控制器时，需要获得系统的全部状态变量，显然在实际中很难满足用全部状态变量构成自适应控制律。因此，只根据被控对象的输入和输出来设计MARS的自适应律，具有非常重要的实际意义。

1) 设被控对象的输入输出方程：

yp(s)=Gp(s)u(s)

(1)

其传递函数：

(2)

式中： Gp(s)——严格真的；Kp——增益参数；Zp(s)，Rp(s)——m阶和n阶首一化古尔维茨多项式(稳定的)。

2) 参考模型的输出方程：

ym(s)=Gm(s)r(s)

(3)

其传递函数：

(4)

式中： Km——常数；Zm(s)，Rm(s)——m阶和n阶首一化古尔维茨多项式；Gm(s)——最小相位系统。根据图1，可以得到可调参数的典型结构，如图2所示。

辅助信号发生器F1，F2均用n-1阶向量微分方程来描述：

(5)

W(1)=cTV(1)

(6)

W(2)=d0yp+dTV(2)

式中： Λ——(n-1)(n-1)稳定矩阵。

F1和F2的传递函数分别是W1(s)，W2(s)：

(7)

(8)

从参考输入r到对象输出的传递函数：

(9)

由此，如果下面各式成立：

N(s)=Zm(s)

[N(s)+C(s)]Rp(s)+KpZp(s)[d0N(s)+

D(s)]=Rm(s)Zp(s)

则： 能够保证可调系统的传递函数与参考模型的传递函数相一致。

图2　n*=n-m=1时的控制方案

为了应用Lyapunov稳定性理论来设计自适应律，要把可调系统和参考模型用状态方程来表达，找出两者状态偏差的动态方程和输出偏差的动态方程，设计出使被控对象和参考模型的输出偏差渐近收敛于零的自适应律。用w(t)T表示被控系统中的可测信号向量，即：

w(t)T=[r(t)， V(1)(t)， yp(t)， V(2)(t)]

(10)

式中： w(t)——2n维向量。由图2可以得到被控对象的综合输入信号u(t)可以写成θT(t)w。再设被控系统的状态方程和输出方程分别为

(11)

yp=hTXp

则增广的被控系统可表示为

(12)

yp=hTXp

在此，假设位置参数θ(t)是分数阶的时变量，设它具有最简单的分数阶模型，不妨定义θ(t)=Dαφ(t)+θ*，其中θ*表示可调参数的真值，φ(t)=D-α(θ(t)-θ*)，它是某种时变量。因此，此时整个被控系统就是分数阶的系统，上述状态方程可以表示为

(13)

式中：

分数阶微分方程是整数阶微分方程的推广，不仅能够更好地划出可调参数的变化规律，更重要的是把可调参数误差用分数阶的微分方程来表示，可以设计出更丰富的自适应律。

当Dαφ(t)≡0即θ(t)=θ*时，式(13)代表真实被控系统的模型。如果用Xmc代表增广参考模型的状态变量，则增广参考模型的状态方程和输出方程可表示为

(14)

从而，被控对象和参考模型的增广状态误差方程为

(15)

设被控对象输出与模型输出间的误差为e1，即

构造Lyapunov函数为

(16)

(17)

自适应律选为

(18)

于是有:

(19)

只要Ac为稳定矩阵，总存在正定矩阵Q和p，使得

(20)

从而，DαV<0。上述所表示的自适应律能够保证分数阶闭环系统是全局渐近稳定的。

(21)

(22)

自适应控制律为

(23)

式(23)表示一类控制律，可以通过选择不同的α值，得到一系列不同的自适应律，来满足不同的控制要求，以改善系统的动态性能。

2．3分数阶模型参考自适应控制器参数对控制系统的影响

由式(23)有

(24)

根据模型参考自适应结构图，可以得到如图3所示的分数阶模型参考自适应结构。

在图3中，Gm(s)为参考模型传递函数；G(s)为被控对象传递函数；r为参考输入信号；u为控制信号；y为闭环系统的输出；ym为参考模型的输出；θ为参数向量；λ为自适应增益；α为自适应控制器的阶次，这里取0<α<2。因此，在分数阶模型参考自适应控制中有2个可调变量： 自适应律的阶次α和可调控制器参数λ。当α=1时为整数阶模型参考自适应控制。

图3　分数阶积分模型参考自适应算法示意

通过调节参数α和λ的大小，得到的仿真图如图4所示。

由上述仿真结果可知，通过调节参数α和λ的大小，完全可以消除分数阶所产生的稳态误差，且随着α的减小，总可以找到合适的λ使系统的性能优于传统的整数阶模型参考自适应控制。

a) α=1．2， λ=0．1时的分数阶模型参考输出　　b) α=1， λ=0．2时的分数阶模型参考输出

3结论

1) 由于有2个调节参数α和λ，分数阶模型参考自适应控制器可以取得比整数阶模型参考自适应控制器更好的动态性能。

2) 常规的模型参考自适应控制为分数阶模型参考自适应控制的特例。根据被控对象的阶次的不同，可以选择不同的α和λ值，以得到最佳控制效果。由于α和λ的值可以连续地变化，因而分数阶模型参考自适应控制更具有灵活性。

当前各领域工业现场采用的控制器整数阶控制器，所以分数阶控制器分析与设计的理论与技术突破将可能带来闭环控制器的发展。

参考文献：

[1]韩增晋.自适应控制[M].北京： 清华大学出版社，1995.

[2]陈新海，李言俊，周军.自适应控制及应用.西安： 西北工业大学出版社，1998.

[3]NAREBDRA K． S, TAYLOR J． H． Frequency Domain Criteria for Absolute Stability． New York： Academic, 1973.

[4]OUSTALOUP A， LEVRON F， MATHIEU B， et al． Frequency-band Complex no Integer Differentiator： Characterization and Synthesis． IEEE Transaction on Circuit and Systems-I： Fundamental Theory and Applications， 2000， 47(01)： 25-39．

[5]OUSTALOUP A， MOREAU X， NOUILLANT M． The Crone Suspension． Control Engineering Practice, 1996， 4(08)： 1101-1108.

[6]ZENG Q S， CAO G Y， ZHU X J． The Effect of the Fractional-order Controller’s Order’s Variation on the Fractional-order Control Systems//Proceeding of the First International Conference on Machine Learning and Cybernetics． Beijing： 2002．

[7]王振滨，曹广益，朱新坚．分数阶定常系统的稳定性及判据．控制理论与应用，2004，21(06)： 922-926．

摘要：自适应控制系统能够辨识外界环境条件或系统本身变化， 自动修正控制系统参数或控制作用， 使系统达到预期状态。介绍了模型参考自适应控制系统(MRAS)的基本结构和控制原理，利用系统的输入输出设计了分数阶控制器，并针对参数未知的线性系统，通过构造新的含有分数阶微分项的Lyapunov函数，设计了一种新的自适应控制律，详细介绍了其设计步骤，并证明了该自适应控制律的有效性。

关键词：分数阶控制器模型参考自适应Lyapunov函数自适应律

Fractional-order Model Design Referring Self-adaptive Control Law with Lyapunov TheoryBai Zhenlong1， Liu Chuanlai2

(1． CNOOC Shandong Chemical Engineering Co． Ltd．， Jinan， 250101， China;

2． College of Automation and Electronic Engineering， Qingdao University of

Science & Technology， Qingdao， 266042， China)

Abstracts： Self-adaptive control system can identify changes from outside environmental condition or system itself and automatically revise control system parameters or control function to make system achieve expected situation． Basic structure and control theory of model reference self-adaptive control system (MRAS) are introduced． Fractional-order controller is designed utilizing system’s input-output, aiming at linear systems with unknown parameters， a novel self-adaptive control law is designed by constructing a new Lyapunov function containing fractional order differentioction options． Detailed design steps are introduced with validated efficiency of the self-adaptive control law．

Key words：fractional-order controller; model reference self-adaptive; Lyapunov function; self-adaptive law

中图分类号：TP273

文献标志码：B

文章编号：1007-7324(2015)05-0043-05

作者简介：白珍龙(1981—)，男，山东沂水人，2008年毕业于青岛科技大学检测技术及自动化装置专业，获硕士学位，现就职于中海油山东化学工程有限责任公司，从事自控设计工作，任工程师。