自动装填机械手的运动学分析与仿真

2015-02-26陈龙淼蒋清山

兵器装备工程学报 2015年5期

梁亮，陈龙淼，蒋清山

(南京理工大学机械工程学院，南京 210094)

在无人化作战平台领域，弹药自动装填机器人是一项关键技术，在火炮的射速、可装填角度、弹丸种类选取准确度等方面有着较大影响，直接影响火炮的射速，自动化程度和可靠性等技术指标和性能。为满足大口径火炮射速要求，需要对自动装填机械手的运动规律进行研究，使其能够在预定的轨迹下运动更快速、准确且平缓，进而实现系统控制［1］。

本研究利用Matlab工具建立了机械手的运动学方程，并对其进行了轨迹规划，为验证其正确性，又利用动力学软件RecurDyn对模型进行了仿真，验证了运动学方程与轨迹规划的正确性，这也是以下众多运动学分析文献中所缺少的验证部分，在验证正确性后，在此指导下也加工出了物理样机。如文献［2］中介绍了Matlab Robotics Toolbox在机器人学仿真实验教学中的基本应用，包括齐次坐标变换、机器人对象构建、机器人运动学求解以及轨迹规划等;文献［3］中在理论的基础上对排爆机械手模型进行了运动学分析与仿真;文献［4］中利Matlab、Robotics Toolbox工具箱对SCARA机器人进行了轨迹规划与仿真;文献［5］中基于ADAMS软件讨论了一种三自由度水下机械手运动学仿真的问题，以上都缺少对运动学方程正确性的验证环节。

本文将以某大口径自行火炮自动装填机械手为例，采用D-H参数方法建立运动学方程，利用Matlab对其进行轨迹规划，在RecurDyn环境中建立仿真模型，对比所得到数据并验证设计的合理性。

1 结构及动作流程

1.1 机械手的结构介绍

自动装填机械手的主要作用是将弹丸从弹仓中取出，并准确地放入输弹机中，机械手主要由基座、回转体、平移体组成，其三维结构如图1所示。

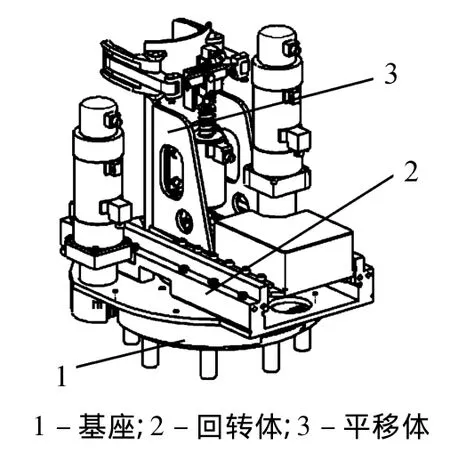
图1 机械手的三维模型

由机械手的三维模型图可以看出，机械手有2个自由度，基座固定，回转体与基座之间为转动关节，回转体可绕基座进行0°～360°旋转，机械手能够在初位——取弹位——输弹位之间旋转。平移体与回转体间为移动关节，平移体能够沿回转体伸出或收回，使得安装在平移体上的抱爪能够在转动关节到位后，伸出抓弹或放弹。通过2个关节的交替配合动作，达到抓弹送弹的工作目标。机械手的机构简图，如图2所示。

图2 机械手的机构简图

1.2 机械手的动作流程

在火炮进行连发射击时，从取弹开始，机械手回转体先从初始位置(零位)旋转85°到取弹位，即弹仓位置，平移体前伸400 mm，到达弹仓中的弹筒，取弹抱爪张开以抓弹，抓取弹丸后，平移体带弹后退400 mm，回转体反向转动85°到达初始位置(即输弹位)，待输弹机到位后，平移体带弹前伸200 mm至输弹机位置，交弹完毕后，平移体无弹后退200 mm至初始位置，等待下一个弹循环。

2 建立机械手运动学方程

2.1 D-H参数的确立

Denavit-Hartenberg(D-H)模型表示了对机器人连杆和关节进行建模的一种非常简单的方法，可用于各种机器人构型，而不管机器人的结构顺序和复杂程度如何。并且D-H方法有其附加的好处，使用它已经开发了许多技术，例如，雅可比矩阵的计算和力分析等。假设机器人由一系列关节和连杆组成。这些关节可能是滑动(线性)的或旋转(转动)的，它们可以按任意的顺序放置并处于任意的平面。连杆也可以是任意的长度(包括零)，它可能被扭曲或弯曲，也可能位于任意平面上。所以任何一组关节和连杆都可以构成一个想要建模和表示的机器人。为此，需要给每个关节指定一个参考坐标系，然后，确定从一个关节到下一个关节(一个坐标系到下一个坐标系)来进行变换的步骤。如果将从基座到第一关节，再从第一关节到第二关节直至到最后一个关节的所有变换结合起来，就得到了机器人的总变换矩阵。按照D-H法，来确定机械手的关节参数即D-H参数［6－8］。

图3 D-H参数法建立的坐标系

首先分析该机械手结构，按照D-H参数法建立各个关节的附体坐标系，惯性参考系在固定在基座上，坐标系o1x1y1z1固定在回转体，坐标系o2x2y2z2固定在平移体的取弹抱爪上，各刚体坐标系间的关系如图3所示。根据建立好的连杆坐标系可得到如表1所示的连杆参数。

表1 机械手D-H参数表

表1中:θi:关节变量。关节变量是指两相邻杆件相对位置的变化量。转动关节为 θi，移动关节为 di;αi:杆件的扭角。相邻两杆件运动轴之间的夹角;ai:杆件的长度。两相邻关节转轴轴线之间公垂线长度。当两轴线相较于一点时，ai=0;di:偏置量。相邻两杆在该关节上的距离。若关节为旋转关节，则di为常量。

2.2 确立A矩阵

A矩阵是相连杆件坐标系的齐次坐标变换矩阵，它是杆件N坐标系向杆件N+1坐标系变换矩阵。

根据表1中的关节参数，带入式(1)可以确立机械手各关节的Ai矩阵，Ai描述第i个连杆，相对于机械手基坐标系的位姿

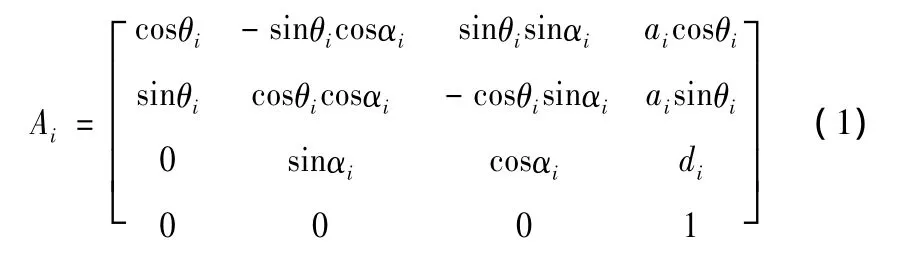
由式(1)以及表1中确定的关节参数可得机械手的A矩阵

2.3 建立运动学方程

将所得A矩阵代入式(2)，即

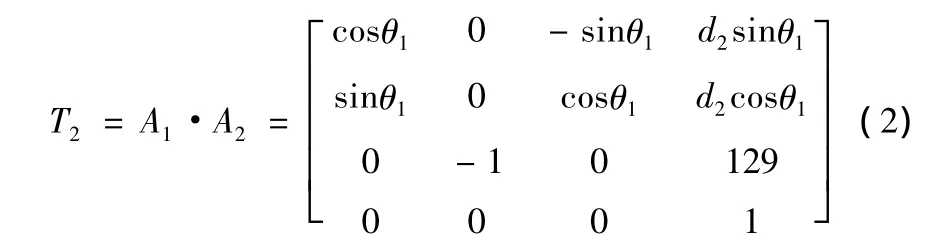
得到机械手的运动方程。由机械手模型可以看出，末端执行器，即取弹抱爪，与平移体是固连的，所以在得出运动学方程后由几何关系容易得到末端执行器的运动规律。

3 运动学仿真

3.1 构建模型

利用Matlab中的Robotics Toolbox工具箱，可以较为方便地建立机械手的杆件三维模型，对之后进行的运动分析与轨迹规划提供了便利。Matlab Robotics Toolbox工具箱是由澳大利亚科学家Peter Corke开发和维护的一套基于Matlab的机器人学工具箱。Robotics Toolbox提供了机器人学研究中的许多重要功能函数，包括机器人运动学、动力学、轨迹规划等。该工具箱可以对机器人进行图形仿真，并能分析真实机器人控制时的实验数据结果，因此非常适宜于机器人学的研究。

根据表1中列举出的机械手相关参数，利用link、robot等函数建立该机械手三维模型，如图4。图4中1号关节为转动关节，2号关节为移动关节，两关节均处于初位，即转动关节没有转动量，移动关节没有伸出量。

下面对Matlab所建立的运动学模型的正确性进行验证:

选取机械手从初位到取弹位这一单一动作流程进行编程，利用Matlab中的fkine等函数，编写程序，

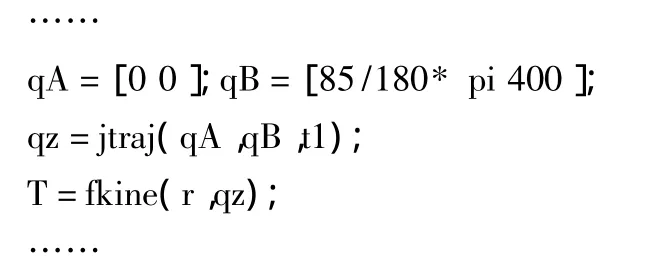
通过对比机械手从初位到取弹位取弹这一动作所求得的齐次变化矩阵的理论解与Matlab所得解，可验证2.3节中所求得的T矩阵理论解的正确性，以及各个关节D-H参数的选取的合理性。

图4 机械手三维模型

3.2 轨迹规划

轨迹规划，又称为移动机器人路径规划技术。指机器人按照某一性能指标搜索一条从起始状态到目标状态的最优和近似最优的无碰路径。可分为2种类型:基于环境先验信息的全局路径规划和基于传感器信息的局部路径规划。后者环境是未知或部分未知的，即障碍物形状、尺寸和位置等信息必须通过传感器在线获取。全局路径规划的主要方法有:可视图法、自由空间法、环境地图法和栅格法等。局部路径规划的主要方法有:人工势场法、遗传算法和模糊逻辑算法等。

轨迹规划［9］是根据自动装填机械手要完成的抓弹任务设计机械手各关节的运动规律，其目的是使装填系统运动平稳、避免碰撞与冲击，且控制系统易于实现。根据前面所确定的机械手抓弹动作流程，对机械手在一个弹循环的连续路径进行分析，观察各个关节的运动规律。

利用Matlab中的Robotics Toolbox工具箱，对机械手在一个完整弹循环内的运动轨迹进行仿真，由于篇幅限制，只观察转动关节1的位移、速度、加速度随时间变化的仿真图像，如图5～图7所示。

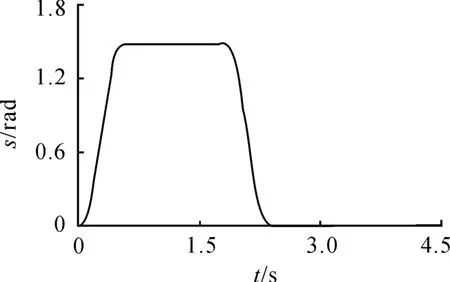
图5 关节1角位移

图6 关节1角速度

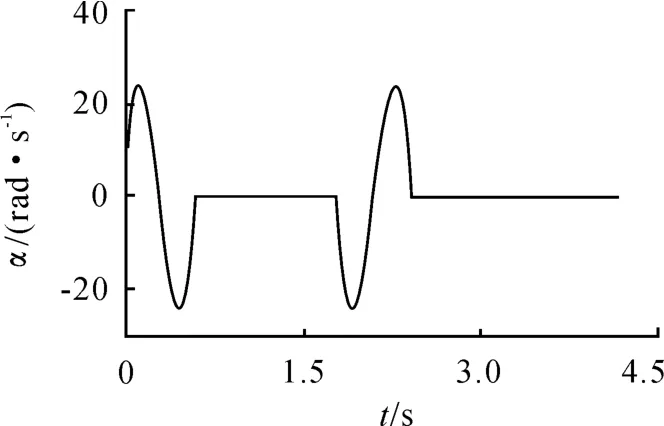
图7 关节1角加速度

3.3 基于Recurdyn的仿真分析

RecurDyn是一种多体动力学仿真软件，它采用相对坐标系运动方程理论和完全递归算法，适合于求解大规模的多体系统动力学问题。本研究将使用RecurDyn对自动装填机械手进行运动学分析，以验证模型设计的合理性，也为后续动力学分析提供了重要依据。

在对自动装填机械手进行三维建模后，将模型导入动力学仿真软件Recurdyn［10］中，以机械手为研究对象，对机械手的三维模进行简化，例如将减速器，编码器等结构去除，以加快之后仿真的速度。在基座与groud之间定义fixed约束，在转动体与基座之间定义revolute约束，在平移体与转动体之间定义translational约束，约束定义后，在revolute和translational约束中添加驱动，机械手运动学模型如图8所示。

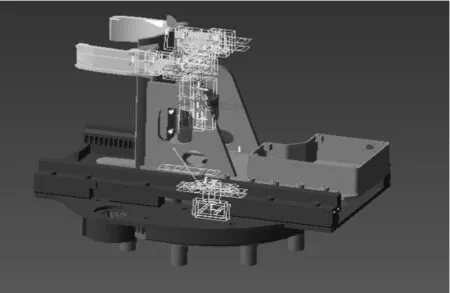
图8 机械手在RecurDyn中的模型

前处理完毕后，对模型进行仿真，设置仿真End time为4.5 s，step为 450。仿真完毕，在 plot result选项中，选择jionts关节1进行角位移，角速度，角加速度的曲线图形的绘制(图9～图11)，并观察机械手在一个弹循环内，转动关节1的运动规律。

图9 关节1角位移

图10 关节1角速度

图11 关节1角加速度

将模型在Recurdyn中仿真所测得的转动关节1运动参量曲线与Matlab绘制的在规定轨迹下，各关节运动参量曲线进行对比，可以看出，在一个弹循环内，关节1的角位移，角速度，角加速度的最大最小值基本相同，同样的，所得到移动关节曲线也相同，这验证了在Recurdyn环境中，虚拟样机模型的正确性，为后面要进行的动力学参数仿真建立了基础。