两种园林绿化植物的分枝格局

靳冰洁, 程栋梁, 马玉珠, 林江铭, 陈燕芬

(福建师范大学 a. 地理科学学院, b. 湿润亚热带山地生态国家重点实验室培育基地, 福建 福州　350007)



两种园林绿化植物的分枝格局

靳冰洁a,b, 程栋梁a,b, 马玉珠a,b, 林江铭a, 陈燕芬a

(福建师范大学 a. 地理科学学院, b. 湿润亚热带山地生态国家重点实验室培育基地, 福建 福州350007)

摘要:了解并研究绿化植物夹竹桃(Nerium indicum Mill)和鸡蛋花(Plumeria rubra cv acutifolia)的生态空间利用能力,旨在更好地制定、实施种植培育策略.以校园种植的夹竹桃与鸡蛋花为研究对象,各选取样木分别采用分枝结构参数分析法,以及WEB模型水平分枝法进行测量分析,在此基础上,探讨这两种园林绿化植物的分枝结构特征.研究结果表明:①不同基径大小的夹竹桃和鸡蛋花分枝数目普遍为4~5枝,两种植物的总体分枝率均在0.90~1.10之间,分枝能力基本一致.②夹竹桃各级分枝长度所表现出的组间差异性整体上要比鸡蛋花情况复杂.各级基径大小的夹竹桃平均分枝角度变化范围在34.00°~46.33°之间,鸡蛋花的平均分枝角度变化范围在56.00°~78.33°之间,且两种植物各级分枝角度在组间的差异较小.③根据WEB模型的假设计算夹竹桃和鸡蛋花的分枝半径指数a和分枝长度指数b值,结果显示夹竹桃a均为正值,且与理论值1/2不存在显著差异;而鸡蛋花的a则均与理论值差异显著.然而夹竹桃和鸡蛋花的b值,由于存在子枝分枝长度大于母枝分枝长度的情况,因此得到的结果出现异常负值,与WBE模型假设存在出入.

关键词:夹竹桃; 鸡蛋花; 分枝率; 分枝结构; WEB模型

对树木构筑型的研究由来已久.从20世纪70年代植物学家Halle 和Oldeman提出树木的构筑型概念并总结出热带树木的23种构型模式以来,人们对树木的构型已经进行了广泛的研究[1-2].树木的构型受到植物内部基因和外部环境的共同影响,表现形态各异[3].植物的构筑型主要由其枝系形态结构决定,植物枝系对植株的外部形态、空间结构、养分运输、树冠形状以及生物量累积起着极为重要的作用[4-5].植物枝系结构的空间位置基本是由生长过程中的3个形态学性状决定的,即枝长、分枝角度和分枝率.它们影响着植物的分枝格局,进而导致植冠构型的差异[6-9].代谢生态学模型植物分型网络(简称WEB模型)利用分枝半径指数、分枝长度指数及代谢速率来研究植物分枝状况,提出植物中存在理想的分枝指数,a=1/2,b=1/3.之后有研究表明:植物的实际分枝状况不符合空间充满和运输能量最小消耗的假设,导致小个体植物的代谢指数接近1.0,而大个体植物的代谢指数小于1.0[10].

夹竹桃(NeriumindicumMill)、鸡蛋花(Plumeriarubracvacutifolia)均为夹竹桃科植物.前者为常绿灌木或小乔木,喜光及温暖湿润气候,广泛种植于亚热带及热带地区;后者为落叶小乔木,适宜于湿润、阳光充足的环境生长,主要在我国西双版纳及东南亚一带广泛种植.此两种植物均具有观赏性,普遍用于园林绿化的培植管理.

目前,国内外开展的植物的分枝结构研究主要聚焦于不同发育阶段和不同生境下的植物分枝结构差异,对乔木树种构型的定量分析处于起步阶段,且结合枝系发育特征、生理整合的研究也较少[11-13].本文选取福建师范大学校园内绿化植物夹竹桃和鸡蛋花为研究对象,运用参数分析法和WEB模型法,分析夹竹桃和鸡蛋花的分枝角度、枝长以及分枝率等参数,探讨植物的分枝格局特征.这有助于了解其分枝结构及生长状况,从而为该两种园林绿化植物的种植培育和生长管理提出合理的经验指导.

1研究地概况及研究方法

1.1　研究区概况

本文研究地点位于福州市闽侯县福建师范大学旗山校区内.实验区位于福建省中东部,地理位置为119°20′E,26°03′N,地貌以冲积平原为主,周围有丘陵和低山,海拔3~10 m.属于中亚热带温热湿润性气候,年平均气温14.8~19.5 ℃,7月最热月均温为23.6~29.3 ℃,1月最冷月均温为6~10.5 ℃,年平均降雨量为2 152.6 mm.实验区位于市区周边,冬暖夏凉,气候温暖湿润,土质疏松,土壤肥力较高,分布多种园林绿化植物,共计135属187种.

1.2　数据测量及分枝结构参数测定

分别选取待测定的夹竹桃,鸡蛋花样木各8株,并按照基径由小到大进行顺序编号(1~8).为保证植物生长状况良好,采样时尽量选取生长空间及采光较好的株样,以避免植株间的生长资源利用状态存在明显差异.测量时,主要使用钢卷尺、游标卡尺等工具测定样株基径、分枝半径、分枝长度;利用量角器和半圆仪测定分枝角度.进行WEB模型的参数估计时,在每株样株上选择分枝长势良好的主侧枝,逐一测量每一级的分枝半径、分枝数、分枝角度,每个样株测定到第三级分枝.依据植物的分型特征,在测量分枝结构的参数时选取生长较为完整的主侧枝进行测量.枝序的确定是分枝结构参数测量的基础,确定方法主要有两种:一种是按植株分枝发育顺序的离心法,另一种是侧重于生理功能的Strahler法(向心法)[14-15].本文采取Strahler法,把植株最外层的小枝定为一级枝,两个一级枝相遇合并则为二级枝,两个二级枝相遇合并则为三级枝.若有不同的枝级相遇,汇合后则以较高枝级为准,以此计算总体分枝率和逐步分枝率[16-17].

总体分枝率计算如下:

(1)

式中:OBR为总体分枝率;NT=∑Ni为测量所有枝级中枝条总数;NS为最高级枝条数;N1为第1级的总枝数.

逐步分枝率为该级与下一高级别枝条数目之比:

(2)

式中:SBRi∶i+1为逐步分枝率;Ni、Ni+1分别为第i级和第i+1级的枝条总数.

数据处理分析采用软件SPSS 19.0,作图使用EXCEL 2013软件.

1.3　WEB模型分枝结构测定

WEB模型认为,植物内部水分的流动导致能量降至最小,且植物从枝干到叶柄的养分传输随着分枝序级逐级进行[18],且分枝结构主要由分枝数、基径及末端基径和分枝长度组成.West,Brown和Enquist曾对分枝半径指数a,分枝长度指数b和生长代谢指数θ之间的关系进行研究,以期找到一个普遍适用的模型来阐释分枝指数a、b与生长代谢间的最适关系[19-20],并指出可能存在理想的植物分枝模型,即当模型参数a=1/2,b=1/3,θ=3/4[21-22].在WEB模型中,将最外侧的小枝视作子枝,也即Strahler法的一级枝,由外向内汇合,直至最后一级枝,称为母枝.另因本文主要探讨植物的分枝格局,故而主要根据WEB模型测量实验数据的参数a,b值,代谢指数θ在此不多做研究.各具体参数指标计算如下:

(3)

(4)

(5)

(6)

(7)

式中:rdaughter、rparent分别表示子枝的基径、母枝基径;ndaughter、nparent分别表示子枝的分枝数、母枝的分枝数;ldaughter、lparent分别表示子枝的分枝长度、母枝的分枝长度;anode、bnode分别表示各级分枝的分枝半径指数、分枝长度指数.

2结果与分析

2.1　分枝率

分枝率作为一个重要指标,其在植物的构型研究中,显示了枝条的分枝能力和各个枝级之间的生理配置状况[23-24].通常逐步分枝率越高,则该级别枝条的分枝能力越强, 空间资源利用程度越高.

对不同基径大小的夹竹桃和鸡蛋花样株分别发生的1~4级和1~5级分枝数目分组进行统计,按照式(1)和式(2)分别计算其总体分枝率和逐步分枝率(表1).结果发现:2种植物样株基径由小到大的总体分枝率差异并不显著(p>0.05),表明所有的样株的总体分枝能力基本一致.但夹竹桃组2和组3之间的逐步分枝率SBR1:2表现出显著差异(p<0.05).鸡蛋花的分枝级数大于夹竹桃,且3种不同基径大小的夹竹桃都表现出第二级、第三极分枝率最大,分枝能力最强.而鸡蛋花的情形与之相反,在所有枝级的逐步分枝率SBR中,不同基径的鸡蛋花其SBR2:3的值均为最小,该情况可能与二者的生长环境和种内竞争有关.夹竹桃株间距较小,靠近基径部分分枝能力较低;第二级、第三级分枝时,能够获取更多光照和资源利用空间,逐步分枝率增大.而位于树木末端,光照充足,空间资源竞争较少,逐步分枝率和总体分枝率较小,主要向上生长,具有顶端优势.鸡蛋花的第一级分枝和植株下端由于枝条拓展空间和阳光充足,逐步分枝率较大.相对而言鸡蛋花的中部空间存在资源制约,逐步分枝率略有起伏,分枝能力不一.

表1　不同基径大小的夹竹桃、鸡蛋花分枝率

注:同物种组间进行比较,字母相同者表示差异不显著(p>0.05).

2.2　不同枝级分枝长度和分枝角度

分枝角度是树木形成的基本要素,对树木冠型的构成起着决定性作用,同时制约着树木的空间分布情况.一般来说, 分枝角度与光照存在着密切关系,其随着枝深度的增加而增大[25].

不同基径大小的夹竹桃一级枝和二级枝长度均表现出显著差异(p<0.05),三级枝的长度在组1和组3之间差异不显著(p>0.05).鸡蛋花的一级枝和二级枝在组1和组2之间都没有显著差异(p>0.05),但不同基径大小的夹竹桃二级枝长度和鸡蛋花一级枝长度内部之间存在显著差异(p<0.05)(表2).根据统计结果总体看来,对于同组的夹竹桃和鸡蛋花植株个体,不同等级的分枝长度并没有呈现出规律的单一递增或递减模式,且夹竹桃的各级分枝长度整体与鸡蛋花的各级分枝长度差距不大,该种情况可能与其生长环境有关.

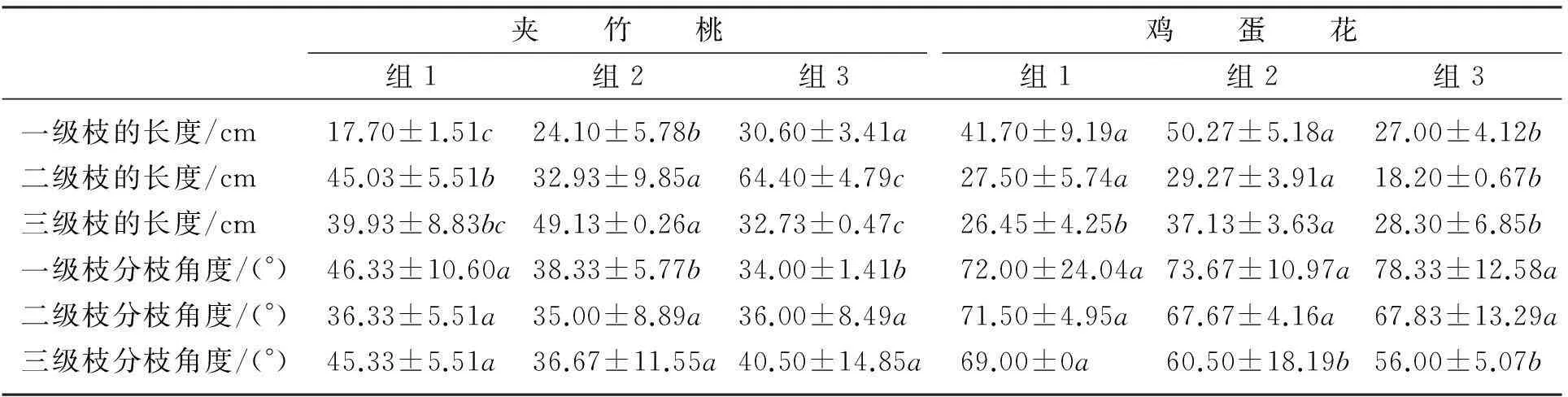
表2　不同基径大小的夹竹桃、鸡蛋花不同枝级的分枝长度和分枝角度

注:同物种组间进行比较,字母相同者表示差异不显著(p>0.05).

不同基径大小的夹竹桃分枝角度整体大约在30°~50°之间,鸡蛋花的分枝角度在60°~80°之间,其总体分枝角度范围大于夹竹桃的分枝角度.除了夹竹桃组1的一级枝及鸡蛋花组1的三级枝分枝角度外,其余各级分枝角度均无显著差异(p>0.05).夹竹桃组1和组2分枝角度从一级枝到三级枝呈现先减小后增加的趋势,而夹竹桃组3则呈现递增趋势.而相似基径大小(同组)的鸡蛋花均表现出分枝角度随分枝级别递减的趋势.

2.3　基于WEB模型的分枝水平分析

在WEB模型中,分枝半径指数a和分枝长度指数b是该模型的两大重要参数,a值主要与植株的各级末端基径和分枝数相关;b值则与植株的各级末端基径和分枝长度相关,且根据模型假设,a,b值均为正值且小于1.0.基于WEB模型的夹竹桃和鸡蛋花不同分枝等级的参数a,b值根据前文提及的式(3)~式(7)进行计算,其参数结果与理想值的差异性见表3.

表3　夹竹桃、鸡蛋花不同分枝等级的WEB模型参数a、b值

注:p-1/2表示参数a与理论值的差异显著性;p-1/3表示参数b与理论值的差异显著性.

分析发现,夹竹桃的分枝半径指数a随着分枝级数逐级递减,且各分枝半径指数a均与理论值1/2没有显著差异(p>0.05).而分枝长度指数b则在第二、三级分枝出现了负值,与假设不符合.这主要是由于各级分枝长度变化造成的(图1).鸡蛋花的分枝半径指数a与分枝级数之间没有明显的递增递减规律.半径指数a虽然均为正值,符合模型假设,但与理论值均存在显著性差异(p<=0.001).第一、第二级分枝的分枝长度指数b值也均与理论值1/3无显著差异(p>0.05).但是第三级分枝的b值也出现了与夹竹桃类似的负值情况,与模型假设不符合.导致该种现象的原因可能与夹竹桃类似,即由于各级别分枝长度不规律所致(图2).

图1　不同基径大小夹竹桃的各级分枝长度变化

图2　不同基径大小鸡蛋花的各级分枝长度变化

3讨论

植物在生长发育过程中所表现的形态,受到进化、自身的生理结构影响,同时植物各部分构件的发育模式由于外部环境的差异具有一定的可塑性[26-27].研究分枝格局旨在了解植物不同构件及整体对空间资源的利用情况,为更好地指导植物生长和制定适宜的生长策略提供合理有效的建议.

夹竹桃和鸡蛋花不同基径大小的个体其总体分枝率(OBR)和逐步分枝率(SBR)基本不存在显著性差异,说明分枝能力在种内较为一致.但从整体上看,鸡蛋花的整体分枝级数要大于夹竹桃,这可能是由于总体上鸡蛋花的个体大于夹竹桃的个体.不同基径大小的夹竹桃和鸡蛋花在同级分枝中并没有呈现出随个体由小至大的规律递增趋势.这可能与植物个体生长环境及获取利用阳光等资源能力的不同有关.此外,不同分枝级别的夹竹桃和鸡蛋花个体其分枝角度近似,差距很小.但是同组(个体大小相似)鸡蛋花的分枝角度则明显表现出了自一级分枝至三级分枝递减的趋势.植物分枝角度的大小是资源环境利用程度的反应,分枝角度越大表明植物充分利用了环境资源以维系其生长.鸡蛋花整体较大,具有更大的生物量,需要更多的生存空间和养分及资源.夹竹桃植株密度小,资源竞争大,当养分不能满足现阶段生长时,主要向上发育,分枝角度变小,生长到一定高度通过拓展横向空间获取阳光等资源,分枝角度逐步增大,呈现出分枝角度由大减小再增大的趋势.

本文还采用WEB模型来探讨样本植物的分枝水平特征.WEB模型假设参数分枝半径指数a和分枝长度指数b为正值,且提出参数a、b与理论值1/2和1/3.本文研究发现,除了夹竹桃第二、三级和鸡蛋花的三级分枝长度指数b外,均符合WEB模型的假设.从整体看,两物种的参数a、b与理论值存在一定差异,且参数b值还有负值.这主要与夹竹桃和鸡蛋花的各级分枝长度变化波动性大有关.根据WBE模型假设,植株的母枝长度基本上长于子枝的分枝长度,分枝长度从植株样本的末端向靠近基径处的各级变化应是呈逐渐递减的趋势,相邻的分枝长度之比小于1.而从图1、图2的观察发现,夹竹桃、鸡蛋花某些样本个体存在第一级分枝长度大于其他子枝分枝长度的现象,而中间各级分枝长度呈波动起伏态势,出现多个母枝长度比子枝分枝长度短的现象,导致b值出现负值.

此前对于不同物种的枝系构型已有不少报道,多从不同发育阶段、竞争类型和地形因子等角度进行研究.由于本文的研究对象主要涉及不同个体大小的成熟形植株,存在一定局限性.因此若需准确了解夹竹桃和鸡蛋花在生存环境中的应对策略,还需开展更加深入的研究.

4结论

通过对不同分组夹竹桃和鸡蛋花的总体、逐步分枝率、各级分枝长度、分枝角度和WEB模型参数的分析,发现此两种植物的总体分枝率均在0.90~1.10之间,且差异不显著,分枝能力较为一致.但是夹竹桃一、二级枝的逐步分枝率(SBR2∶3)组间略有差异.同时,随着分枝数目增加,逐步分枝率有所下降,资源利用率降低.不同枝级的分枝长度和分枝角度在组间差异性较为明显(p<0.05).WEB模型分析结果表明夹竹桃和鸡蛋花的分枝半径指数a,前者与理论值1/2差异性不显著(p>0.05),而后者与理论值差异均显著(p<0.05).夹竹桃第一级分枝半径指数b与理论值1/3差异显著(p<0.05),鸡蛋花前两级分枝半径指数b与理论值差异不显著(p>0.05),夹竹桃第二、三级分枝和鸡蛋花第三级分枝的分枝半径指数b则存在负值情况,与WEB模型假设不符.

参考文献:

[ 1 ]HalléF,OldemanRAA,TomlinsonPB.TropicalTreesandForests:AnArchitecturalAnalysis[M].NewYork:Springer-Verlag, 1978.

[ 2 ] 任艳林. 海南主要热带树木苗期构筑型研究[D]. 北京:北京林业大学, 2004.

(Ren Yanlin. The Study on Architecture of Main Tropical Tree Seedlings in Hainan[D]. Beijing: Beijing Forestry University, 2004)

[ 3 ] 臧润国,蒋有绪. 热带树木构筑学研究概述[J]. 林业科学, 1998,34(5):112-119.

(Zang Runguo, Jiang Youxu. Review on the Architecture of Tropical Trees[J]. Scientia Silvae Sinicae, 1998,34(5):112-119)

[ 4 ] Nelson N D, Burk T, Isebrands J G. Crown Architecture of Short-Rotation, Intensively Cultured Populus: I. Effects of Clone and Spacing on First-order Branch Characteristics[J]. Canadian Journal of Forest Research, 1981,11(1):73-81.

[ 5 ] 郇慧慧,胥晓,刘刚,等. 不同分枝数对桑树幼苗生长发育的影响[J]. 生态学报, 2014,34(4):823-831.

(Huan Huihui, Xu Xiao, Liu Gang et al. Effect of Branch Number on the Growth and Development of Morus alba Saplings[J]. Acta Ecologica Sinica, 2014,34(4):823-831.)

[ 6 ] 何丙辉. 银杏构件生物学理论与应用[M]. 北京:中国林业出版社, 2001.

(He Binghui. Theories and Application of Modular Biology in Ginkgo biloba[M]. Beijing: Forestry Press of China, 2001.)

[ 7 ] 孙书存,陈灵芝. 辽东栎植冠的构型分析[J] . 植物生态学报, 1999,23(5):433- 440.

(Sun Shucun, Chen Lingzhi. Architectural Analysis of Crown Geometry in Quercus liaotungensis[J]. Chinese Journal of Plant Ecology, 1999,23(5):433-440.)

[ 8 ] 钟章成,曾波. 植物种群生态研究进展[J]. 西南师范大学学报:自然科学版, 2001,26(2):230-236.

(Zhong Zhangcheng, Zeng Bo. Trends and Advances in Researches on Plant Population Ecology[J]. Journal of Southwest China Normal University:Natural Science, 2001,26(2):230-236.)

[ 9 ] 赵相健,王孝安. 太白红杉分枝格局的可塑性研究[J]. 西北植物学报, 2005,25(1):113-117.

(Zhao Xiangjian, Wang Xiaoan. Study on Branching Pattern Plasticity of Larix chinensis[J]. Acta Botanica Boreali-Occidentalia Sinica, 2005,25(1):113-117.)

[10] Cheng D L, Li T, Zhong Q L, et al. Scaling Relationship between Tree Respiration Rates and Biomass[J]. Biology Letters, 2010,6(5):715-717.

[11] 何明珠,张景光,王辉. 荒漠植物枝系构型影响因素分析[J] . 中国沙漠, 2006,26( 4):625- 630.

(He Mingzhu, Zhang Jingguang, Wang Hui. Analysis of Branching Architecture Factors of Desert Plants[J]. Journal of Desert Research, 2006,26(4):625-630.)

[12] Oohata S, Shidei T. Studies on the Branching Structure of Trees: I. Bifurcation Ratio of Trees in Horton’s Law[J]. Japanese Journal of Ecology, 1971,21(1/2):7-14.

[13] 陈波,宋永昌,达良俊. 木本植物的构型及其在植物生态学研究中的进展[J]. 生态学杂志, 2002,21(3):52-56.

(Chen Bo, SongYongchang, Da Liangjun. Woody Plant Architecture and Its Research in Plant Ecology[J]. Chinese Journal of Ecology, 2002,21(3):52-56.)

[14] Whitney G G. The Bifurcation Ratio as an Indicator of Adaptive Strategy in Woody Plant Species[J]. Bulletin of the Torrey Botanical Club, 1976(103):67-72.

[15] Zhu X, Ye Y. Architectural Analysis of Crown Geometry in Quercus variabilis[J]. Henan Science, 2000,19(1):65-67.

[16] 何明珠,王辉,张景光. 民勤荒漠植物枝系构型的分类研究[J] . 西北植物学报, 2005,25(9):1827 -1832.

(He Mingzhu, Wang Hui, Zhang Jingguang. Classification of the Branching Architectures of the Desert Plants in Minqin County[J]. Acta Botanica Boreali-Occidentalia Sinica, 2005,25(9):1827-1832.)

[17] 孙书存,陈灵芝. 不同生境中辽东栎的构型差异[J] . 生态学报, 1999,19(3):358-364.

(SunShucun,Chen Lingzhi. The Architectural Variation of Quercus Liaotungensis in Different Habitats[J]. Acta Ecologica Sinica, 1999,19(3):358-364.)

[18] Bentley L P, Stegen J C, Savage V M, et al. An Empirical Assessment of Tree Branching Networks and Implications for Plant Allometric Scaling Models[J]. Ecology Letters, 2013,16(8):1069-1078.

[19] West G B,Brown J H,Enquist B J. A General Model for the Origin of Allometric Scaling Laws in Biology[J]. Science, 1997,276(5309):122-126.

[20] West G B,Brown J H,Enquist B J. A General Model for the Structure and Allometry of Plant Vascular Systems[J]. Nature, 1999,400(6745):664-667.

[21] Niklas K J, Enquist B J. Invariant Scaling Relationships for Interspecific Plant Biomass Production Rates and Body Size[J]. Proceedings of the National Academy of Sciences, 2001,98(5):2922-2927.

[22] 马玉珠,程栋梁,钟全林,等. 7种木本植物的分支指数与代谢指数[J]. 植物生态学报, 2014,38(6):599-607.

(MaYuzhu, Cheng Dongliang, Zhong Quanlin, et al. Branching and Metabolic Exponents in Seven Woody Plants[J]. Chinese Journal of Plant Ecology, 2014,38(6):599-607.)

[23] Borchert R,Slade N A. Bifurcation Ratios and the Adaptive Geometry of Trees[J]. Botanical Gazette, 1981:394-401.

[24] 林勇明,洪涛,吴承祯,等. 桂花植冠的枝系构型分析[J]. 热带亚热带植物学报, 2007,15(4):301-306.

(LinYongming,Hong Tao,Wu Chengzhen. Architectural Analysis of Osmanthus fragrans Crown Geometry[J]. Journal of Tropical and Subtropical Botany, 2007,15(4):301-306. )

[25] 肖锐,李凤日,刘兆刚. 樟子松人工林分枝结构的研究[J]. 植物研究, 2006,26(4):490-496.

(XiaoRui,Li Fengri,Liu Zhaogang. Branching Structure Analysis of Mongolian Pine Plantation[J]. Bulletin of Botanical Research, 2006,26(4):490-496. )

[26] Harper J L. The Concept of Population in Modular Organisms[M]∥ Theoretical Ecology: Principles and Application. Sunderland, MA:Sinauer Associates Inc. Publishers, 1981:53-77.

[27] 林勇明,俞伟,刘奕,等. 不同距海处木麻黄分枝格局特征及冠形分析[J]. 应用与环境生物学报, 2013(19)4:587-592.

【责任编辑: 曹一萍】

(LinYongming,Yu Wei,Liu Yi, et al. Characteristics of Branching Pattern and Crown Morphology of Casuarina equisetifolia L. in Different Coastal Distances[J]. Chinese Journal of Applied and Environmental Biology, 2013,19(4):587-592.)

Branching Structures of Two Garden Plants

JinBingjiea,b,ChengDonglianga,b,MaYuzhua,b,LinJiangminga,ChenYanfena

(a. College of Geographical Sciences, b. State Key Laboratory Breeding Base of Humid Subtropical Mountain Ecology, Fujian Normal University, Fuzhou 350007, China)

Abstract:The abilities of utilizing ecological space of oleander (Nerium indicum Mill) and frangipani (Plumeria rubra cv acutifolia) were studied to formulate and implement the planting and cultivation strategy preferably. Sample individuals were chosen respectively and analyzed by using horizontal branching structure parameters method and WEB model analysis method. On this basis, the branching structural characteristics of the two plants were probed into. The results show that: ①Different basal diameter of oleander, frangipani had the similar branching number, which was mostly 4~5. And both of the overall bifurcation ratios were between 0.90 and 1.10, the branching probabilities were basically the same. ②The branching length of differences between groups of oleander was more complex than that of frangipani as a whole. The mean branching angle of different basal diameter of oleander was between 34.00°~46.33°, and the mean branching angle of different basal diameter of was between 56.00°~78.33°. The differences of the two plants’ branching angle between groups are small at all levels. ③The branching radius index “a” and the branching length index “b” of oleander and frangipani are calculated according to WEB model, the results indicated that, “a” value of oleander were all positive, and there were no differences with the 1/2 of theoretical value; while all “a”values of frangipani appeared significant differences with the theoretical value. However, due to existing situations that secondary branches were longer than primary branches, “b” values of both oleander and frangipani exhibited abnormal negative, this had a discrepancy with the assumption of WEB model.

Key words:oleander; frangipani; bifurcation ratios; branching pattern; WEB model

收稿日期:2014-12-14

中图分类号:S 688

文献标志码:A

作者简介:靳冰洁(1990-),女,江苏南京人,福建师范大学硕士研究生; 程栋梁(1980-),男,陕西西安人,福建师范大学教授,硕士生导师.

基金项目:国家自然科学基金资助项目(31170374,31170595,31370589); 福建省教育厅新世纪优秀人才支持计划(JA12055); 福建省杰出青年基金资助项目(2013J06009).

文章编号:2095-5456(2015)02-0120-06