中国经济波动率对经济增长率非对称影响效应的实证分析

张屹山，田依民

（1.吉林大学 数量经济研究中心，吉林 长春130012；2.吉林大学 商学院，吉林 长春130012）

一、引 言

长期以来，宏观经济学对于经济增长和经济周期波动这两个问题是分别来研究处理的，并发展出了各自部分相对成体系的若干理论。根据新古典增长理论，长期经济增长率的提高有赖于投资率、劳动力增长率以及技术进步等供给方面的提升，并没有强调经济短期波动情况对于长期经济增长的影响。在真实经济周期理论出现之前，新凯恩斯理论认为经济的短期周期波动主要是消费、投资或者货币供应量等名义因素造成总需求波动所致，供给方面的实际因素似乎不会对短期周期波动带来影响。而真实经济周期理论则认为技术进步增长率的波动情况等供给方面的因素也会成为短期经济波动的来源。然而，目前还没有形成一个相对完善的理论体系，来解释经济增长和经济周期波动之间的关联性。短期经济波动程度和不同经济周期阶段对于长期经济增长的影响等问题的研究对于科学合理地制定兼顾短期和长期的经济政策具有重要意义。

对于短期波动和长期增长关联性的现有研究主要集中在短期波动性大小对于长期经济增长的影响如何，而且不同的研究对此也未能给出一致的结论。经济波动大小一般用经济增长率、产出缺口标准差、增长核算方程残差的标准差、GARCH 类模型和经济增长的在险水平等方法来度量。在理论模型研究方面，有一些研究得出的结论是经济波动程度会对经济增长产生正向影响效应。Black（1987）从风险和收益的角度阐述了短期波动性对于长期经济增长的影响，认为高风险预期的技术投资往往伴随着高预期回报。如果投资新技术的预期回报能够补偿投资者的预期风险，那么投资者就会增加这些新技术的投资，这样一来经济波动越大很可能意味着更高的长期经济增长率［1］。有一些理论模型认为经济波动性和经济增长之间的影响关系是不确定的，可能会随着其他变量而变化。Blackburn（1999）在一个具有干中学特征的内生增长模型中对于经济波动程度对经济增长的正向影响进行了证明。相对地，另一些研究则认为经济波动程度对经济增长产生的是负向影响［2］。陈昆亭等（2012）建立一个包含人力资本的内生随机增长模型，证明了如果人力资本形成中主观过程占优时，波动程度会对经济增长产生正向影响；如果人力资本自然形成占优时，波动程度则对长期经济增长产生负向影响［3］。

经济波动与经济增长之间影响关系在实证研究中也同样存在着两种结论。Grier等（2004）建立了一个向量自回归移动平均、GARCH 均值模型，考察了产出和通货膨胀率波动性对于产出和通货膨胀率水平的影响。结果表明，产出波动性对产出平均增长率产生的是正向影响效应，产出和通货膨胀率对于波动性的正向和负向冲击的动态反应都存在着非对称性效应［4］。Berument等（2012）利用土耳其1987年第一季度至2007年第三季度的数据，检验了经济波动性和经济增长率之间的关系。结果表明，增长的波动性会降低经济增长，而且这样的结果在不同设定的情况下都是稳健的［5］。Cerra和Saxena（2007）利用跨国面板数据，实证分析了经济波动性和经济增长率之间的影响关系。结果表明，经济波动性对长期经济增长率的影响是负向的，同时，政治和金融危机对产出的负向冲击所带来的损失是永久的［6］。Martin和Rogers（2000）利用欧洲地区一些国家和OECD 国家的数据分别进行了回归分析，结果表明，经济增长和失业率标准差越大的国家和地区的经济增长率都比较低，即经济波动性对经济增长率带来的是负向影响［7］。Fatás（2002）研究了经济周期和长期经济增长率之间的关系，最后认为短期波动的持续性和长期经济增长率之间存在着正相关关系，但是短期波动性对长期经济增长率产生的却是负向影响［8］。刘金全和张鹤（2003）使用三种方法分别度量了我国经济的波动性，然后对经济波动性与经济增长之间的关系进行了检验，结果表明，我国经济波动性对经济增长存在着正向影响关系［9］。刘金全等（2005）通过ARCH－M 模型和结构VAR模型，对我国经济波动性对经济增长率的影响进行了实证检验，结果表明，经济波动性对经济增长产生了正向的影响效应［10］。卢二坡和曾五一（2008）使用省级数据和面板数据模型，实证检验了我国短期波动和经济增长之间的影响关系。结果表明，两者之间的影响关系可能随着回归方程中控制变量设定的改变而不同，经济波动对经济增长率的影响是非线性的［11］。邵军和徐康宁（2011）通过DEA 方法和面板数据回归模型，对我国经济波动性对生产率的影响进行了分析。结果表明，经济波动对于效率提高的影响并不显著，但是对于技术进步则存在反周期性效应［12］。

综上所述，经济波动率对经济增长的影响在理论模型和实证分析的研究中均存在两种不同的结论，目前尚未形成统一的共识。国内这方面的研究鲜有涉及在不同经济周期阶段下，经济波动率对经济增长率的影响是否一致的问题。本文拟在以前研究的基础上，分析经济增长波动率对经济增长率溢出效应的非对称特征。具体地，首先利用GARCH（1，1）－M 模型初步分析经济波动性对经济增长率的影响方向。然后通过两区制马尔科夫区制转移模型来确定各期属于经济扩张期还是经济收缩期，最后通过带有虚拟变量的GARCH（1，1）－M 模型来分析经济增长波动率在不同经济周期阶段对经济增长率的影响效应是否显著不同。

二、经济波动率与经济增长率关联性的数理分析

根据Blackburn和Galindev（2003）的分析，在不同的技术进步形成机制下，经济波动率与经济增长率之间的影响关系是不同的［13］。模型假设经济中是由大量相同且无限生命的人组成的，他们生产和消费单一产品。每一个人以最大化自身效用做出最优选择，一生贴现的效用函数具体表示如下：

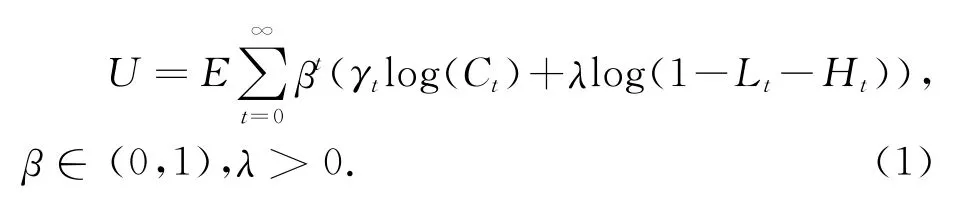
约束条件如下：

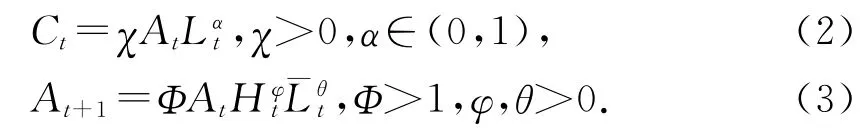
其中，Ct表示消费，At表示生产率或者技术水平。由于经济中只生产一种产品且忽略了资本生产要素，所以所有产品都被用于消费。式（2）表示的是经济中的生产性约束，同时包含了产品市场均衡条件。γt表示消费偏好的平稳随机冲击，其均值和方差分别为μγ和σ2γ。个体从消费Ct和休闲1－Lt－Ht中获得正效用，其中，Lt表示个体在产品生产中的劳动时间投入，Ht表示为了提高生产率At而进行学习的劳动时间投入。式（3）表示的是实现技术进步的两种途径，即内部学习和外部学习。内部学习也被称作主动学习，表示为了提高生产效率而进行的科研活动等；而外部学习又被称作被动学习，主要体现了“干中学”的思想，即人们在劳动过程中会无意识地逐渐提高劳动生产率，也可以简单地理解为熟能生巧。¯Lt表示总就业水平，在式（3）中体现了技术进步中的“干中学”效应。在这个数理模型中，经济增长是由技术进步驱动的，而技术水平的进步则是通过内部学习和外部学习来实现的。如果φ＝0并且θ＞0，表示技术进步完全是通过外部学习实现的；如果φ＞0并且θ＝0，则意味着技术进步完全是内部学习的结果。模型参数的不同所导致的这两种极端情形在后面的分析中会涉及。

通过对上述最优化问题的Lt和Ht求解，可以得到以下两个方程：

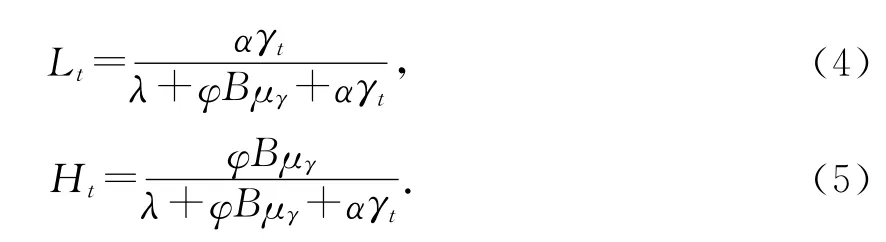
其中，B＝β／（1－β）。从式（4）和式（5）中可以看出，Lt随着γt的增加而增加，Ht则随着γt的增加而减少。一个正向的需求冲击会增加消费的边际效用，导致从事提高生产率的内部学习活动的机会成本增加，这样人们增加更多生产的劳动时间投入，相对地减少为了技术进步而学习的劳动时间投入。

将式（4）和式（5）的结果代入到式（2）和式（3）中，同时利用均衡条件Lt＝¯Lt，就可以得到技术水平和产出增长率如下的表达式：

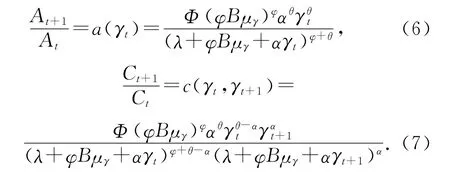
技术进步的形式会决定需求冲击对技术进步率的影响方向。如果技术进步完全来自内部学习（φ＞0，θ＝0），根据式（6）可以看出，技术进步率会随着γt的增加而降低，这就说明技术进步率是反周期变化的。相反地，如果技术进步完全来自外部学习（φ＝0，θ＞0），那么技术进步率会随着γt的增加而提高，这说明技术进步率是顺周期变化的。根据式（7）可以看出，产出增长率的变化不仅取决于t期的需求冲击，还与t＋1期的冲击有关。一个γt的正向冲击会增加当期生产劳动投入，同时减少内部学习的劳动投入，但是对于At＋1的影响方向却是不确定的。这就意味着Ct会增加，但是Ct＋1可能增加或者降低，从而产出增长率可能升高或者降低。在技术进步完全依赖内部学习（φ＞0，θ＝0）的特殊情形下，t期正向的需求冲击会提高产出增长率；而在外部学习（φ＝0，θ＞0）的特殊情形下，t期正向的需求冲击对产出增长率的影响方向则取决于参数θ和α的大小关系。由于γt＋1的正向冲击会提高t＋1 期的生产劳动投入Lt＋1，从而提高t＋1 期的产出Ct＋1，所以t＋1期需求的正向冲击会使得产出增长率升高。

根据式（7），可以得到如下两个表达式：

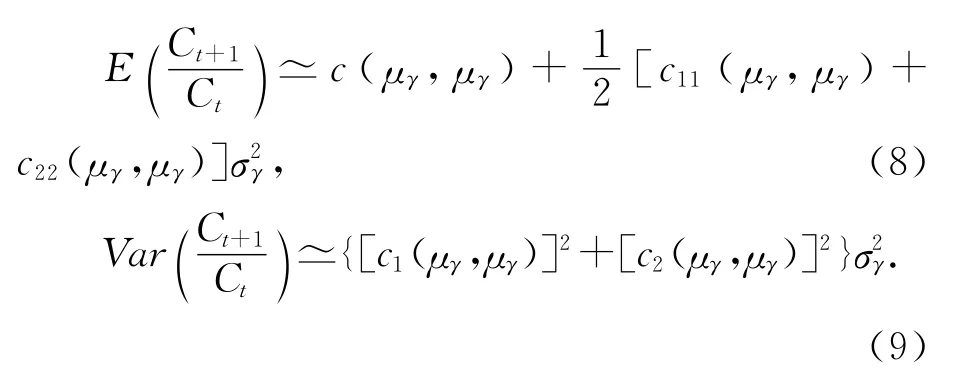
从式（9）可以看出，产出增长率的方差与随机需求冲击的方差σ2γ是正相关的。从式（8）可以看出，如果令f（φ，θ，α）＝c11（μγ，μγ）＋c22（μγ，μγ），那么函数f（φ，θ，α）的符号会决定产出增长率的均值与随机需求冲击方差σ2γ之间正相关或负相关的关系，具体表达式如下：

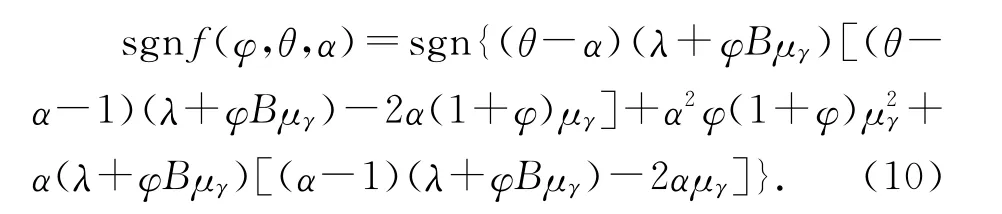
和之前的分析一样，这里依然着重讨论两种典型的技术进步形式对函数f（φ，θ，α）符号的影响。在技术进步完全来自内部学习（φ＞0，θ＝0）的情形下，函数f（φ，θ，α）的符号为正，也就是说此时产出增长率的均值E（Ct＋1／Ct）和方差Var（Ct＋1／Ct）之间应该存在正向的影响关系。而在技术进步完全来自外部学习（φ＝0，θ＞0）的情形下，函数f（φ，θ，α）的符号则取决于参数之间的大小关系。在众多的参数关系组合中，θ＞α是f（φ，θ，α）＜0的充分条件。

由以上分析可以看出，经济波动率对经济增长率的影响关系很可能取决于技术进步来自主动学习还是被动学习。田依民和于洪菲（2014）为了估算潜在经济增长率而构建了一个包含生产函数的状态空间模型［14］。在模型的技术进步变化方程中，考虑了研究与实验发展经费支出、实际利用外资和劳动力投入对技术水平的影响。其中，科研活动投入费用对应着上面理论模型中的内部学习的含义，劳动力投入则对应着理论模型中的外部学习的含义。实证结果表明，劳动力投入对技术水平的影响是显著的，而研究与实验发展经费支出对技术水平的影响却是不显著的。这说明我国技术进步主要来自外部学习的形式，即“干中学”效应在我国是非常明显的。由于上面的数理模型中生产函数省略了资本，同时我国主动学习的劳动投入样本长度过短，这就为直接估计模型中的主要参数带来了困难。虽然上面数理模型和状态空间模型表示主动学习的变量不同（在状态空间模型中代表内部学习的变量选择的是科研活动投入费用，而在上面的理论模型中采用的是主动学习劳动时间投入），但是二者表示的经济含义是相同的，所以可以近似地认为数理模型中参数φ＝0，θ＞0是符合我国情况的。同时，状态空间模型的估计结果还表明劳动力对技术水平的影响参数约为0.45，生产函数中劳动力的弹性参数约为0.28，也就是说θ＞α。综上，我国情况应该对应着数理模型φ＝0，θ＞0，θ＞α这样的参数关系。而根据上面理论模型的分析结论，这样的参数关系预言了经济波动率和经济增长率之间负向的影响关系。下面通过实证分析来进一步考察我国经济波动率对经济增长率的影响关系。

三、实证分析

为了实证检验经济增长波动率对经济增长率的影响效应，本文首先利用季度名义GDP 和消费者价格指数得到实际季度GDP 的数据，然后对实际GDP进行季节调整。由于GARCH 族模型需要较多的样本点，所以此处将季度实际GDP进行插值，以得到估算的月度GDP的数据，利用RATS 8.0 软件完成数据频率的转化。然后以此月度GDP 数据算出月度GDP 环比增长率，作为本文实证分析的主要数据。数据区间是1992年1月份至2013年12月份，原始数据从国家统计局网站上获得。

（一）ARCH 效应的LM 检验

在建立GARCH－M 模型之前，需要对数据的聚类异方差性质进行检验，以确定数据是否适合利用GARCH 类模型来建模。具体地，针对以下的回归方程的残差利用Engle的LM 统计量来进行ARCH 效应检验：

其中，gt表示的是月度GDP的环比增长率，参数估计和LM 检验结果分别表示如下：

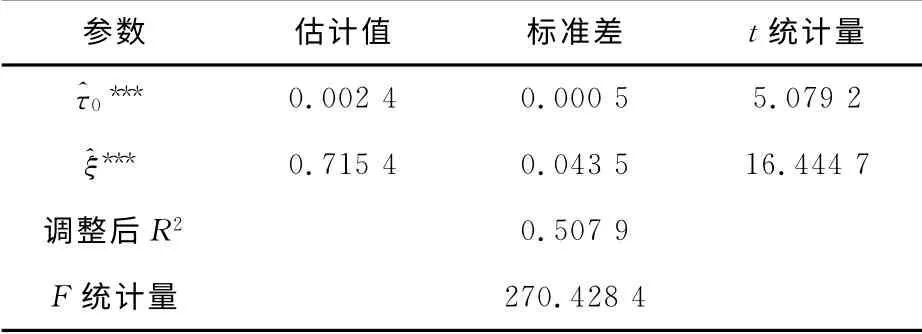
表1 方程（11）的估计结果

表2 Engle检验结果

从表1中可以看出，常数项和自回归系数都是在1%的显著性水平下显著的，F统计量表明方程整体回归在1%的显著性水平下是显著的。从表2中可以看出，T×R2统计量在1%的显著性水平下拒绝了残差序列不存在ARCH 效应的原假设，这表明月度GDP 增长率是存在ARCH效应的，利用GARCH 族模型对其建模是合理的。

（二）GARCH－M 模型的建立及估计

为了考察经济增长波动率对经济增长率的影响效应，可以利用GARCH－M 模型来进行分析。GARCH－M 多用于考察金融资产的风险是否对金融资产收益率产生溢出效应影响。如果将经济增长率看作一国财富增长率，那么经济增长波动率就可以看作是财富增长率的风险。所以GARCH－M 模型可以用来很好地分析经济增长波动率对经济增长率的影响效应。具体建立如下的GARCH（1，1）模型：

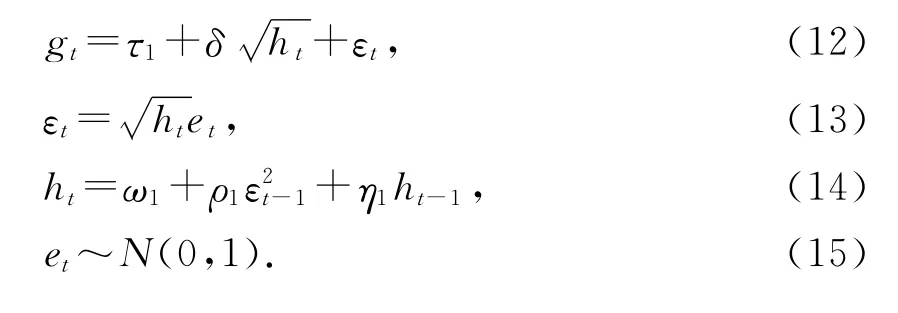
其中，gt表示GDP的月度增长率，et表示服从标准正态分布的白噪声，ht表示残差εt的条件方差，表示εt的条件标准差。参数估计结果具体表示如下：

表3 GARCH－M 模型的估计结果

（三）利用两区制马尔可夫区制转移模型划分经济周期

关于经济周期的划分，主要包括NBER 所使用的非参数方法和Hamilton（1989）提出区制转移模型参数方法［15］。本文此处选择Hamilton（1989）的方法对月度经济增长率建立高增长和低增长两区制的马尔可夫区制转移模型，最后通过计算两个状态的后验概率来得到经济周期划分的结果。具体模型表示如下：

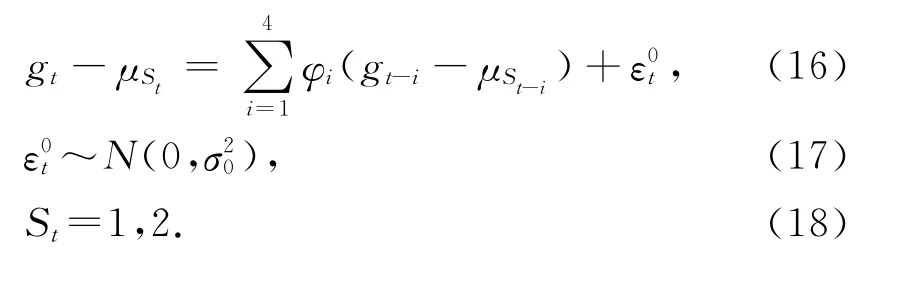
其中，St表示区制状态变量，这里设定St取值为1或2，分别表示高增长区制和低增长区制。概率转移矩阵表示如下：

其中，pij表示从状态j转移到状态i的概率。上面的区制转移模型表示的含义是，在不同的经济周期阶段经济增长率的均值是不同的，μSt表示在不同状态下gt序列的均值。通过识别出不同各期增长率均值所属状态，也就可以得到经济周期划分的结果了。模型参数估计结果表示如下：

表4 马尔可夫区制转移模型估计结果

从表4中可以看出，经济平均增长率在两个状态下是明显不同的。在经济扩张的区制下，月度平均增长率是1.02%；在经济收缩的区制下，平均增长率则为－0.11%。由此，可以定义区制一为经济繁荣扩张区制，而区制二为经济收缩区制。通过区制转移模型虽然并不能确定样本各期处于区制一还是区制二，但是可以算出各期所属区制一和区制二的后验概率。所以可以根据后验概率是否大于0.5来确定各期所属经济扩张阶段还是经济收缩阶段，也就是说，如果某一期区制一后验平滑概率大于0.5，则认定这一期为经济扩张期，反之则认定这一期为经济收缩期。图1表示的是样本内各期所属经济扩张状态和经济收缩状态的后验概率。然后根据概率是否大于0.5，就可以认定各期所处的经济周期阶段，进而得到关于经济周期不同阶段的两个虚拟变量d1和d2。d1在经济扩张期用1 表示，在经济收缩期用0表示，d2则与之相反。这样就可以分析不同经济周期阶段下，经济增长波动率对经济增长率的影响是否有所差异。两区制在样本内各期的后验平滑概率如图1所示：

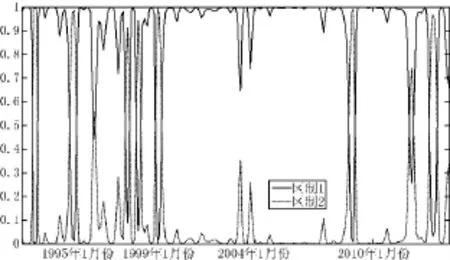
图1 两区制在各期的后验平滑概率

（四）带有虚拟变量的GARCH－M 模型

为了进一步考察经济增长波动率在不同经济周期阶段对经济增长率的影响是否相同，借鉴Kim 和Lee（2008）的模型设定形式，在之前GARCH－M 模型基础上加入表示经济周期不同阶段的虚拟变量［16］。具体模型形式表示如下：

其中，δ1和δ2分别表示在经济扩张期和经济收缩期经济增长波动率对经济增长率的影响。和前面一样，et表示服从标准正态分布的白噪声。参数估计结果表示如下：

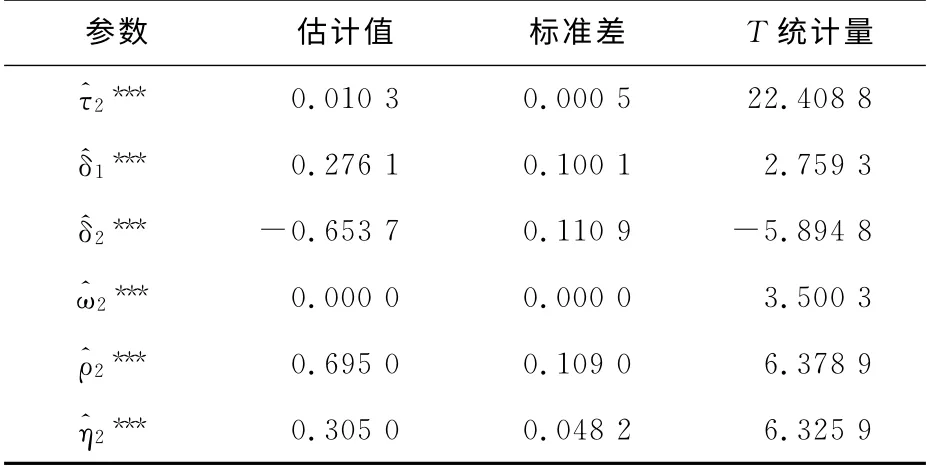
表5 包含虚拟变量GARCH－M 模型的估计结果

从表5中可以看出，δ1和δ2在1%的显著性水平下是显著不为零的。同时，δ1的估计值大于零，δ2的估计值小于零，这说明经济增长波动率对经济增长率产生的是非对称效应。具体而言，当经济处于扩张时期，经济增长波动率对经济增长率产生了正向的显著影响，当经济处于收缩时期，经济增长波动率对经济增长率产生的则是负向的显著影响。同时，δ2估计值的绝对值大于δ1的绝对值，这也就意味着经济增长波动率对经济增长率产生的总体影响效应是负向的，这与前面不带有虚拟变量GARCH－M 的回归结果也是一致的。结合表3的回归结果可以看出，从整体上看，经济增长波动率对经济增长率产生的是负向的显著影响，同时在不同经济周期阶段，这种影响又是显著不同的。可能的原因是在经济扩张时期，企业和个人对当前经济运行状况信心非常充足，对经济前景乐观，而高收益伴随着高风险，此时人们更愿意追求高收益而忽视高风险，从而增加了投资，投资又增加了总需求，使得经济增长率升高。另外，消费者可能由于经济增长风险增加而增加了预防性储蓄，更高的储蓄水平会带来更高的均衡经济增长率。在经济收缩时期，人们对经济运行前景并不乐观，企业和个人变得更加谨慎，相对于高收益，更加重视背后的高风险，所以当表示经济风险的波动率增加时，企业可能会减少投资，总需求降低导致了经济增长率随之降低。这样的结果说明了古典经济学关于经济周期和经济增长“二分法”在我国是不成立的。我国经济周期和经济增长并不是相互独立的经济现象，经济周期的波动情况对经济增长会产生影响。

四、结论及政策启示

本文首先通过一个数理模型分析了经济波动率和经济增长率之间的关联性，对模型中主要参数进行了校准。然后对季度GDP 数据进行月度分解得到GDP 增长率并建立了GARCH（1，1）－M 模型，通过测算可知经济增长波动率对经济增长率产生了负向的影响效应，这也验证了之前数理模型的结论。之后通过马尔可夫两区制转移模型识别出样本内各期所属经济扩张期还是经济收缩期，从而进一步地研究不同经济周期阶段经济增长波动率对经济增长率的影响。带有表示不同经济周期阶段的虚拟变量的GARCH（1，1）－M 模型回归结果表明，经济增长波动率在不同经济周期阶段对经济增长率的影响呈现出非对称性的特征。也就是说，在经济扩张期和经济收缩期，经济增长波动率对经济增长率的影响是显著不同而且方向是相反的。在经济扩张期经济增长波动率对经济增长率产生的是显著的正向影响效应，在经济收缩期经济增长波动率对经济增长率产生的是显著的负向影响效应，而这种负向影响程度要大于正向影响程度。

经济增长波动率对经济增长率的溢出效应具有非对称性特征，这意味着政府在不同的经济周期阶段应当采取不同的政策。从短期来看，在经济扩张繁荣时期，由于经济波动率对经济增长率具有正向的溢出效应，所以当经济运行出现一定的波动性时，政府可以适当减轻短期需求管理政策对经济的“干预”力度，即政策当局在经济扩张期对于一定程度的经济波动不必“过度重视”。在经济收缩低增长时期，由于经济波动率对经济增长率产生了负向的溢出效应，所以政府需要对经济波动情况采取更加关注的态度。即政府在经济收缩时期应该加大需求管理政策对经济的“干预”力度。也就是说，政府在不同的经济周期阶段对待经济波动情况应当采取不同的“容忍”态度。如果政府在决策当期还无法准确判断经济处在扩张期还是收缩期，由于经济增长波动率在整体上对经济增长率的影响效应还是负向的，政府就应当实施以减少经济波动情况的逆周期政策。

［1］ Black F.Business Cycles and Equilibrium［M］.New York：Basil Blackwell，1987.

［2］ Blackburn K.Can Stabilisation Policy Reduce Long－run Growth？［J］.Economic Journal，1999，109（452）：67－77.

［3］ 陈昆亭，周炎，龚六堂.短期经济波动如何影响长期增长趋势？［J］.经济研究，2012（1）：42－53.

［4］ K.B.Crier，Ólan T.Henry，N.Olekalns，K.Shields.The Asymmetric Effects of Uncertainty on Inflation and Output Growth［J］.Journal of Applied Econometrics，2004，19（5）：551－565.

［5］ M.Hakan Berument，N.Nergiz Dincer，Z.Mustafaoglu.Effects of growth volatility on economic performance－Empirical evidence from Turkey［J］.European Journal of Operational Research，2012，217（2）：351－356.

［6］ Cerra V.，S.Saxena.Growth Dynamics：The Myth of Economic Recovery［R］.BIS Working Papers，2007，No.226.

［7］ Martin P.C.，A.Rogers.Long－term Growth and Short－term Instability［J］.European Economic Review，2000，44（2）：359－381.

［8］ Antonio Fatás.The Effects of Business Cycles on Growth［R］.Central Bank of Chile Working Papers，2001，No.156.

［9］ 刘金全，张鹤.经济增长风险的冲击传导和经济周期波动的“溢出效应”［J］.经济研究，2003（10）：32－39.

［10］ 刘金全，付一婷，王勇.我国经济增长趋势与经济周期波动性之间的作用机制检验［J］.管理世界，2005（4）：5－11.

［11］ 卢二坡，曾五一.转型期中国经济短期波动对长期经济增长影响的实证研究［J］.管理世界，2008（12）：10－23.

［12］ 邵军，徐康宁.转型时期经济波动对我国生产率增长的影响研究［J］.经济研究，2011（12）：97－109.

［13］ Keith Blackburn，Ragchaasuren Galindev.Growth，volatility，learning［J］.Economics Letters，2003，79（3）：417－421.

［14］ 田依民，于洪菲.开放经济下中国潜在产出和技术水平的估算——基于Kalman滤波的状态空间模型［J］.经济问题，2014（12）：30－36.

［15］ James D.Hamilton.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle［J］.Econometrica，1989，57（2）：357－384.

［16］ Sei－Wan Kim，Bong－Soo Lee.Stock Returns，Asymmetric Volatility，Risk Aversion，and Business Cycle：Some New Evidence［J］.Economic Inquiry，2008，46（2）：131－148.