基于灰色马尔科夫的径流序列趋势预测

张 锐，马 静

（1.吉林省水文水资源局白城分局，吉林 白城137000；2.吉林省水文水资源局延边分局，吉林 延吉133001）

近些年来，由人类活动带来下垫面改变及大气循环异常使水文要素发生改变，水文要素变异使水文序列的关系也发生了变异[1]，正确分析复杂变化环境下流域各种水文序列变化规律，具有非常重大的现实意义。渭河流域的水文气象要素变化趋势及其影响因子一直受到诸多学者的关注[2]。研究发现，近50年来在气候变化与人类活动的双重作用下，该流域的各水文序列都在不同程度上发生了变异[3]。本文将选取张家山、咸阳、状头、华县4 个水文站，应用灰色马尔科夫模型对渭河流域径流序列的趋势进行预测。

1 模型原理

1.1 GM（1，1）模型

GM 模型[4]是基于灰色系统理论的微分方程，x（0）（k）+az（1）（k）=b 是GM(1，1)模型，表示一阶1个变量的微分方程，式中a，b 为模型参数。

1.2 马尔科夫模型

马尔科夫模型[4]在现代预测方法中占有重要的地位，是利用事物不同状态的初始概率和状态之间转移概率来预测事物未来状态的一种数学方法，具有比较高的准确性、科学性、及适应性。

马尔科夫模型预测过程：首先以原始数据及灰色模型的预测数据为基础，建立状态的划分标准；其次确定转移概率矩阵P，即为P（n）=P（n-1）·P，m 步转移概率Pij（m）（i，j=1，2，…，n）指系统从状态i 经m 步转移到j 的概率；最后根据某年所处状态预测下一年有可能出现状态，再对各个状态所处区间范围进行加权平均，并最终求出灰色马尔科夫预测值。

综上所述，将灰色理论与马尔柯夫链结合起来，形成灰色-马尔柯夫链预测模型，不仅能揭示时间序列的发展变化趋势，并且能预测状态的规律，使预测具有更强的科学性及实用性[5]。

2 灰色马尔科夫模型径流序列趋势预测

以渭河流域各水文站最后一个变异点年份至今的年径流序列为主要研究对象，因其具有一定的随机性，符合灰马尔科夫的研究范围。将各站数据按上述步骤计算可得该模型参数，计算得到各水文站的结果。

2.1 咸阳站径流序列趋势预测

以咸阳站1986—2010年的年径流序列为初始数据，计算出a，b，并将其代入可得GM(1，1)灰微分方程的时间响应序列为：

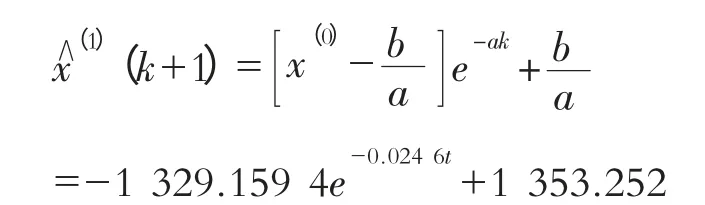
同样采用后验差检验法对该模型进行检验，经过分析计算：P=1，C=0.508。由等级表可知，该灰色模型精度较好。

根据残差的变化范围在-21.25～27.34 之间，将残差划分为5 种状态，其对应区间分别为（-22，-12），（-12，-2），（-2，8），（8，18），（18，28）。

故一步转移矩阵为：

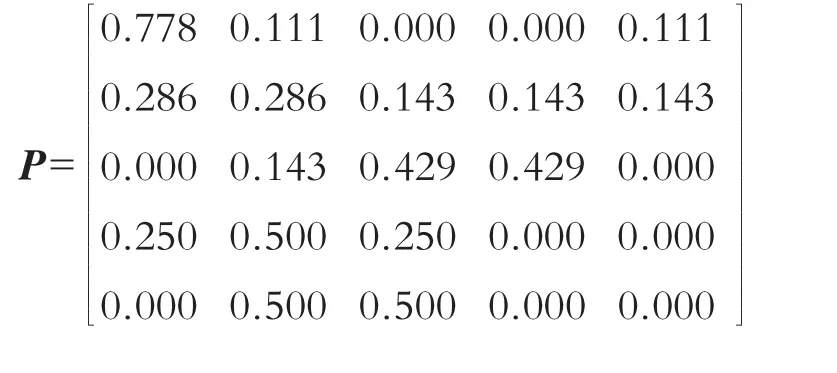
同样以2010年的径流数据预测为例，由于2010年的径流数据处于状态1，则2011年的径流数据处于状态1，2 和5 的概率分别为0.778，0.111和0.111，则可求出2011年的马尔科夫预测值=灰色预测值+［0.778×（-22-12）+0.11×（-12-2）+0.111×（18+28）］=-5。以此类推求出其他年份的马尔科夫预测值。通过计算可得未来45年径流的条件概率分布如图1所示。

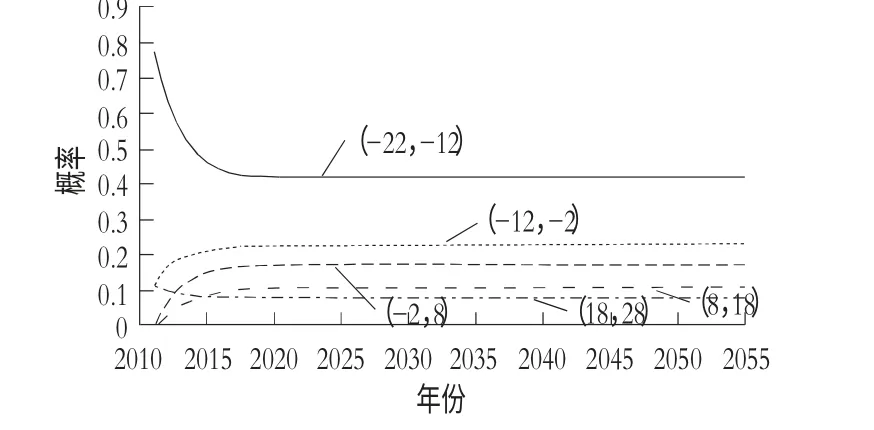
图1 咸阳站未来年径流序列概率分布

由于灰色马尔科夫预测模型函数为减函数，故预测咸阳站未来径流量有减少的趋势；又由于该站未来45年径流量偏向前几种状态，预测径流量较变异后的实测径流量偏少。

2.2 华县站径流序列趋势预测

以华县站1990—2010年的年径流序列为初始数据，计算出a，b 并将其代入可得GM(1，1)灰微分方程的时间响应序列为：

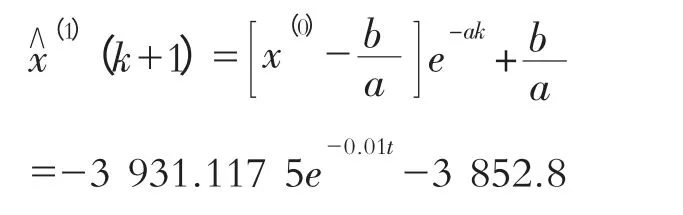
同样采用后验差检验法对该模型进行检验，经过分析计算：P=1，C=0.415。由等级表可知，该灰色模型精度较好。

根据残差的变化范围在-25.13～48.84 之间，将残差划分为5 种状态，其对应区间分别为（-26，-11），（-11，4），（4，19），（19，34），（34，49）。

故一步转移矩阵为：

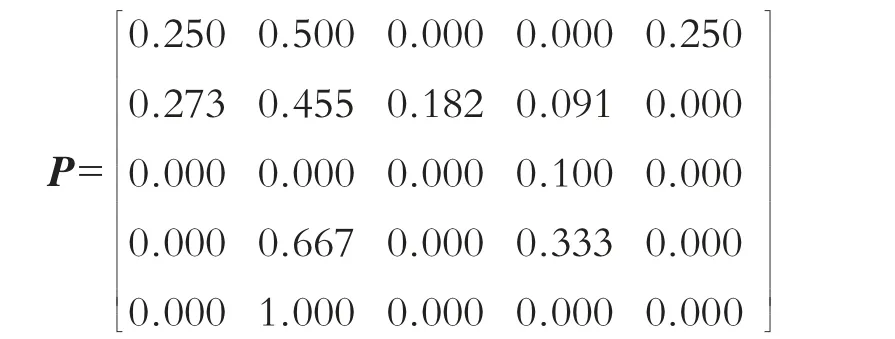
以2010年的径流数据预测为例，由于2010年的径流数据处于状态3，则2011年的径流数据处于状态4 的概率为1，则可求出2011年的马尔科夫预测值=灰色预测值+1×(19+34）=101.26。以此类推求出其他年份的马尔科夫预测值。通过计算可得未来45年径流的条件概率分布如图2所示。

图2 华县站未来年径流序列概率分布

由于灰色马尔科夫预测模型函数为增函数，故预测华县站未来径流量有增加的趋势；又由于该站未来45年径流量偏向前几种状态，预测径流量较变异后的实测径流量偏少。

2.3 张家山站径流序列趋势预测

以张家山站1997—2010年的年径流序列为初始数据，计算出a，b 并将其代入可得GM（1，1）灰微分方程的时间响应序列为：

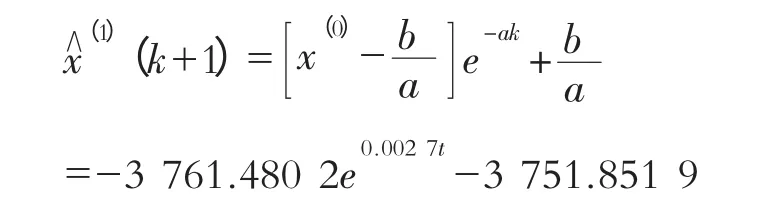
同样采用后验差检验法对该模型进行检验，经过分析计算：P=1，C=0.55。由等级表可知，该灰色模型精度较好。

根据残差的变化范围在-5.71～11.89 之间，将残差划分为5 种状态，其对应区间分别为（-6，-2），（-2，2），（2，6），（6，10），（10，14）。

故一步转移矩阵为：

同样以2010年的径流数据预测为例，由于2010年的径流数据处于状态3，则2011年的径流数据处于状态1 的概率为1，则可求出2011年的马尔科夫预测值=灰色预测值+1×（-6-2）=2.53。以此类推求出其他年份的马尔科夫预测值。通过计算可得未来45年径流的条件概率分布如图3所示。

图3 张家山站未来年径流序列概率分布

由于灰色马尔科夫预测模型函数为增函数，故预测张家山站未来径流量有增加的趋势；又由于该站未来45年径流量偏向前几种状态，预测径流量较变异后的实测径流量偏少。

2.4 状头站径流序列趋势预测

以状头站2002—2010年的年径流序列为初始数据，计算出a，b 并将其代入可得GM(1，1)灰微分方程的时间响应序列为：

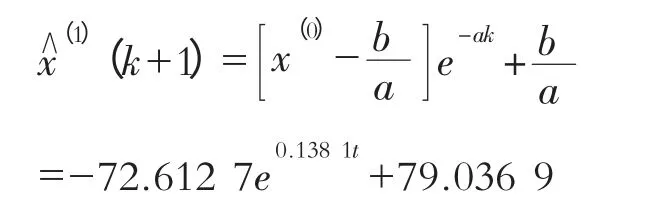
同样采用后验差检验法对该模型进行检验，经过分析计算：P=1，C=0.518。由等级表可知，该灰色模型精度较好。

根据残差的变化范围在-1.96～3.12 之间，将残差划分为5 种状态，其对应区间分别为（-2，-0.9），（-0.9，0.2），（0.2，1.3），（1.3，2.4），（2.4，3.5）。

故一步转移矩阵为：

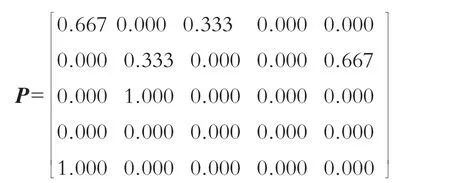
同样以2010年的径流数据预测为例，由于2010年的径流数据处于状态5，则2011年的径流数据处于状态1 的概率为1，则可求出2011年的马尔科夫预测值=灰色预测值+1×(2.4+3.5）=0.2。以此类推求出其他年份的马尔科夫预测值。通过计算可得未来45年径流的条件概率分布如图4所示。

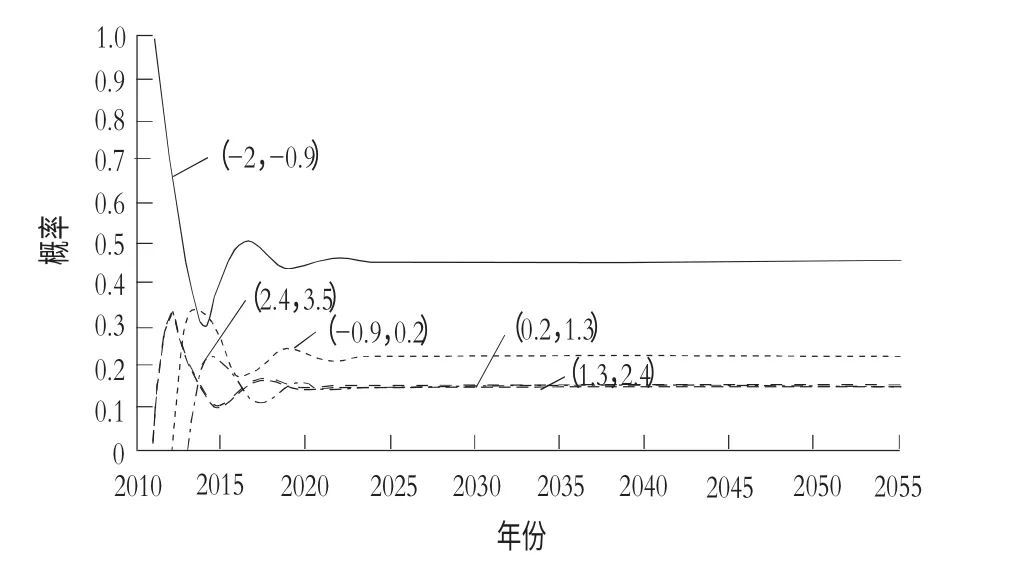
图4 状头站未来年径流序列概率分布

由于灰色马尔科夫预测模型函数为减函数，故预测状头站未来径流量有减少的趋势；又由于该站未来45年径流量偏向前几种状态，预测径流量较变异后的实测径流量偏少。

3 结 语

将灰色理论与马尔科夫模型相结合对渭河流域各典型水文站年径流序列变化趋势进行预测。预测林家村站及咸阳站未来年径流序列有减少趋势，且年径流序列较变异后的实测年径流序列偏少；预测华县站及张家山站未来年径流序列有增多趋势，但年径流序列较变异后的实测年径流序列偏少；预测状头站未来年径流序列有减少趋势，且年径流序列较变异后的实测年径流序列偏少。

［1］ 丁一汇，任国玉，石广玉，等.气候变化国家评估报告(Ⅰ)：中国气候变化的历史和未来趋势［J］. 气候变化研究进展，2006，2（1）：3-8.

［2］ 燕爱玲，黄强，王义民. 河川径流演变的非趋势波动分析［J］. 水力发电学报，2007，26（3）：1-4.

［3］ 佟春生. 复杂性理论在河川径流时间序列分析中的应用研究［D］. 西安：西安理工大学，2005.

［4］ 臧文亚，周仲礼，龚灏，等.基于灰色马尔科夫模型的重庆市水运货运量的预测［J］.水运工程，2012，（1）：30-33.

［5］ 章柏红，谢孔峰.灰色-马尔柯夫链预测建模方法及其应用［J］. 海南师范大学学报(自然科学版)，2008，21（4）：469-471.