新一代溶液几何模型中的关键参数——偏差函数的性质
2015-02-25陈志远周国治王丽君李福燊
陈志远,周国治,2,王丽君,2,李福燊
(1. 北京科技大学钢铁冶金新技术国家重点实验室,北京 100083)(2. 北京科技大学冶金与生态工程学院物理化学系,北京 100083)(3. 北京科技大学材料科学与工程学院,北京 100083)
新一代溶液几何模型中的关键参数
——偏差函数的性质
陈志远1,周国治1,2,王丽君1,2,李福燊3
(1. 北京科技大学钢铁冶金新技术国家重点实验室,北京 100083)(2. 北京科技大学冶金与生态工程学院物理化学系,北京 100083)(3. 北京科技大学材料科学与工程学院,北京 100083)

王丽君
摘要:溶液几何模型是计算多元系溶液、熔体性质的有力工具。几何模型经过发展,已经积累了丰富的计算方法。经过总结和创新,发展出了新一代几何模型。首先提供了溶液几何模型的简明计算图式。通过Sb-Ga二元合金熔体体系与Cu2S-FeS-Ni3S2三元熔融硫化物体系性质计算,分别指出了传统溶液几何模型中对称模型与非对称模型各自的理论缺陷。证明了新一代几何模型在理论上优于传统几何模型。并结合二元完全互溶体系热力学性质之间的关系,分析了新一代溶液几何模型引入的重要参数,针对偏差函数在新一代几何模型中的意义进行了探讨。通过计算与实例明确提出偏差函数的正定性与对称性两个重要性质,并将偏差函数性质数学化。提出了研究热力学函数之间关系的新思路,为几何模型的进一步发展做好必要的理论准备。
关键词:热力学;相图计算;溶液性质;几何模型
1前言
几何模型是一类利用二元体系热力学数据计算三元及多元体系的热力学函数性质的计算方法,在液态合金、有机溶液、熔盐及熔渣性质预报和相图计算上得到了广泛而且成功的应用,具有很强的实用性与精确性[1-7]。几何模型属于半理论半经验模型,经过几十年的发展,很多研究者在热力学理论基础上,通过发展不同的二元系选点计算方法给出了一系列模型。根据二元系的选点方法不同,传统几何模型可以分为对称几何模型和非对称几何模型[8]。其中对称几何模型包括Kohler[9],Muggianu[10],和 Lück-Chou[11-12]等几种模型,非对称几何模型包括Toop模型[13]与Hillert模型[8]等。这两类模型在计算方法上各有优势,但都具有相应的缺点,例如非对称几何模型存在人为干预的因素,而对称模型又有无法还原为二元体系的缺陷。
周国治总结了以上传统模型计算方法[12],提出新一代几何模型[14],给出了更具有普遍意义的新的计算方法。新一代几何模型避免了上述传统几何模型的缺点,并作出更进一步的发展,即引入评价两个二元系性质的参数——相似系数,避免了人为选择组元的干扰,通过平方偏差系数和相似系数给出不同的二元体系热力学函数的权重,从而普遍地适用于热力学函数性质的计算[15]。
如果不采用推荐的相似系数,通过自行设计相似系数计算规则,则可以变化出包括各种传统模型在内的无数种计算方法。而基于平方偏差系数的相似系数计算方法,则是最为普遍采用的。本文对新一代几何模型的理论讨论也是基于这一计算方法开展。
Zhang等[16]对新一代几何模型计算方法做了进一步的简化工作,使得其更易于实现计算机化。
新一代几何模型的理论优势,使其得以广泛应用于多元体系热力学性质研究工作中。如Al-Ni-Zn合金体系中各元素活度[17]及其它合金体系热力学函数计算[3, 18]中,都运用了新一代几何模型。经过发展,模型推广到计算溶液熔体物理化学性质工作中。研究者利用新一代几何模型准确地预测了三元体系的表面张力[19, 20]、电导率[7]、密度[21]及其它性质[5, 22]。
此外,高于三元系的多元溶液体系物理化学性质预测,是几何模型应用的重要发展方向。新一代几何模型由三元向多元扩展时,只需根据二元系的数据逐步叠加,代表点成分的计算在向多元扩展时也完全是线性的。Zhang等[23]发展了四元溶液体系性质的模型预测方法,其研究结果与Hossein等[24]对另一四元体系的研究结果都表明了新一代几何模型,在多元系性质预测上的精准性。
很多研究者在模型预测与实验验证中,对比了新一代几何模型计算结果与传统几何模型计算结果[3, 25-27]。利用实际体系验证模型准确性,是模型选择的重要标准。但是,高温冶金熔体性质测定实验结果,往往具有很大的误差,因此,利用实验结果验证并不是完全可靠。在实际体系性质预测的基础上,还需要结合理论分析模型的自洽性与合理性。
模型中的偏差函数及以此为基础的相似系数,是新一代几何模型由二元体系性质计算更高元体系性质的关键参数。周国治指出了偏差函数是一个与二元系的自由能相差程度有关的非负值量,而且当所计算的两个二元系近似时偏差函数趋于零[28]。这是建立偏差函数的一个主要条件。目前,文献中对几何模型的讨论偏重于拟合效果和预报的准确性,而对偏差函数和相似系数的探讨并不多,尤其对于偏差函数意义的挖掘还有待加深。本文将对偏差函数与度量空间的特征进行对比分析,探讨偏差函数的意义。
2新几何模型计算方法
如图1所示,几何模型依式(1)→式(6)→式(7)由二元系热力学数据计算三元系热力学数据[14]。
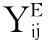
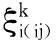

3传统几何模型的缺陷
3.1对称模型的缺陷
对称几何模型将三元系数据还原为二元系之后,同一个二元系成分点会对应多个热力学状态,这与热力学理论是相违背的。以文献[3]中数据为例,假定有伪三元系Sb-Ga-Ga,计算结果如图2所示。在相图中Ga-Ga底线的平行线上的点为相同的化学成分,对应的热力学性质也应相同。图2a、b是分别采用Kolher模型和Muggianu模型计算出的结果,等值线并未与Ga-Ga线平行。即在同一Sb: Ga成分下,Kohler模型与Muggianu模型计算所得的Sb-Ga二元系在同一成分点对应了无数的热力学状态函数值。新一代几何模型的计算结果如图2c所示,可以看出,其计算结果是符合热力学理论的。因此,新一代几何模型不同与对称几何模型,是一个自洽的模型。
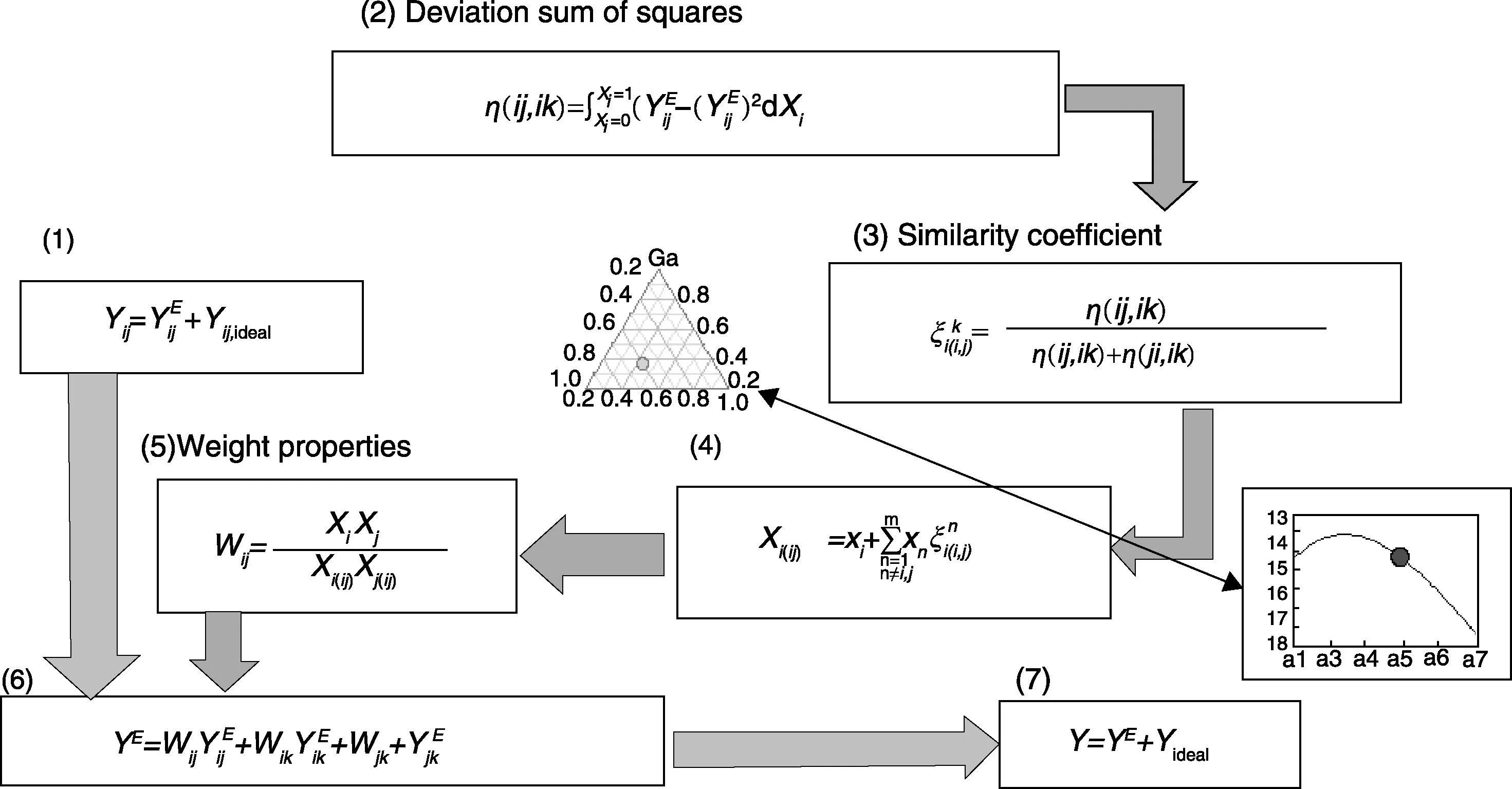
图1 新一代几何模型的计算方法流程图Fig.1 Flow pattern of calculation method of new generation geometric model
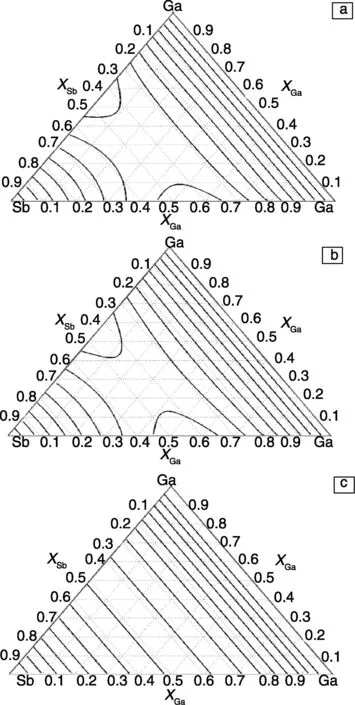
图2 采用不同几何模型计算的1 073 K时Sb-Ga体系中超额吉布斯自由能等值线:(a)Kohler模型,(b) Muggianu模型, (c)新一代几何模型Fig. 2 Equivalent lines of excess Gibbs free energies calculated by three geometrical models for Sb-Ga binary system at 1 073 K: (a)Kohler model, (b)Muggianu model,and (c) new general solution model
3.2非对称模型的缺陷
由于选点方法的非对称性,当计算组元顺序变换后,非对称几何模型计算三元系中相同成分点会对应着不同的热力学函数的计算结果,这也不符合常理。计算者往往会根据经验在这几个计算结果中进行选择,带来人为干预。例如,以文献[20]中数据,通过变化不同的三元系顶点顺序,得到了Cu2S-FeS-Ni3S2体系在特定成分点上的计算结果,如表1所示。对于同一个成分点,非对称几何模型中的Hillert模型和Toop模型在变换取点方式后出现了3种不同的计算结果。因此,非对称模型计算结果并不能保证其可靠性,模型计算过程也不能完全计算机化,它需要辅助验证与经验判断才能获得可能正确的结果。并且,如果未做验证实验或相应实验点过少、实验误差过大,往往会造成误判。

表1 在1 473 K不同取点顺序下不同几何模型计算Cu2S-FeS-Ni3S2的表面张力的结果(N/m)(摩尔分数Cu2S∶FeS∶Ni3S2=0.25∶0.25∶0.5)
4偏差函数与度量
4.1偏差函数的特性
新一代几何模型中偏差函数是以两个二元系性质的平方偏差来表示。文献中述及偏差函数有以下几点重要特性[15, 29];①偏差函数η(ij,ik)所比较的两个二元系有一个共同的组元i,且偏差函数中使用这一公共组元i分别在两个二元系中的摩尔分数作为自变量;②偏差函数η(ij,ik)应为非负值,而且当j和k两个组元无限近似时趋于零。这一特性克服了对称几何模型高元系不能还原为低元系的缺点;③偏差函数η(ij,ik)作为与i-j二元系和i-k二元系的超额热力学函数相差程度有关的量,不受人工干预的影响。这一特性克服了非对称几何模型中权重因子Wij的选择受人为干预的缺点。
可见,偏差函数是克服传统模型缺陷的关键。当某一函数形式符合这3个特性,则有可能用作为偏差函数,应用到新一代几何模型的计算中。
文献中对模型的比较一般限于模型预报结果的比较[20, 25-27, 30-31]。各几何模型对溶液体系的预报结果可能并没有固定的优劣顺序,而且单纯以预报结果比较并不恰当。从偏差函数后两个特性来看,几何模型中没有产生悖论的只有新一代几何模型。
但以上总结的特性只是经验性描述。将偏差函数特性数学化能更进一步的揭示热力学函数性质函数相互之间的关系,并且能严格的证明新一代几何模型与传统模型之间的差别。
4.2超额热力学函数的空间
本节通过超额热力学函数的空间这一概念,引出距离这一概念。如果从理论上发展超额热力学函数的空间,也许可以得以窥见普遍适用的热力学函数之间的关系。
一个包含数个二元系超额热力学函数的集合,可以称为一个空间。计算i-j-k三元系所用的i-j,i-k,j-k三元系所组成的空间Ω则为:i-j, j-i,i-k,k-i,j-k,k-j 6个二元系函数。这一空间Ω具的特性如下所述:
定义空间Ω中任意函数φ的形式为φ(i,j,YE(i)),其中YE(i)为以组元i的摩尔分数为变量的i-j二元系的超额热力学函数,i为YE(i=1)时的初始点相,j为YE(i=0)的终点相;
性质空间Ω中任意函数φ(i,j,YE(i))若初始点相i与函数ψ(k,m,YE(m))终点相m为同一相,且函数φ终点相j与函数ψ初始点相k为同一相,则这两个函数为同一函数,即可表达为φ=ψ;
即,i=m且j=k时,φ(i,j,YE(i))= ψ(k,m,YE(m));
推论φ(i,j,YE(i))=-φ(j, i ,YE(j)) ,即超额热力学函数表现出关于零点的镜像对称性。
上述描述就构成了一个二元超额热力学函数的空间,而偏差函数η(ij,ik)本质上也是表示两个二元系超额热力学函数的相似程度,与泛函中的度量具有相似性,因为度量是两个函数的距离。为方便起见,以下以YE(i)代替φ(i,j,YE(i)),也即i-j二元系中YE(i)= YE(j)。
度量用以下公理定义[32]:非空集合Ζ中,如有任意的x,y,z∈Z,①d(x,y)=0当且仅当x=y;②d(x,y)=d(y,x);③d(x,y)≤d(x,z)+d(z,y)。则称这一非负函数d是集合Ζ的度量,或称距离。集合Ζ赋予度量d称为度量空间。由度量的定义与偏差函数的特性相对比。可以发现,偏差函数的后两个特性与度量的第1条性质正定性,以及度量的第2条性质对称性是一致的。
5偏差函数的意义
偏差函数与度量具有相似性。在度量空间中,也有以平方偏差和作为度量的实数空间。但是实数空间与超额热力学函数的空间具有不同的性质。比如实数空间并没有关于零点的镜像对称性这一性质。因此,在本节中着重讨论偏差函数是否可以作为超额热力学函数的空间的度量,超额热力学函数的空间是否是一个度量空间。
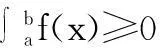
下面证明在超额热力学函数的空间中偏差函数的正定性。
i-j-k三元系中包含的6个超额热力学函数组成的空间里,有3个偏差函数,分别是式(2)与以下两式:
(8)
(9)
偏差函数的正定性证明如下:
① 必要性
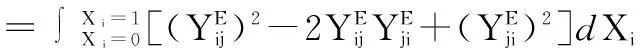
(10)
由于二元系超额热力学函数关于零点的镜像对称性,上式可化为:
=0
(11)
② 充分性
当η(ij,ik)=0时,有:
(12)

(13)

(14)

(15)
证毕。
偏差函数的正定性从数学上说明,新一代几何模型可以使得高元系中任意两个二元系i-j与i-k中的组元j与k在对应的热力学性质无限接近时,偏差函数趋近于零。由于偏差函数的这一性质,新一代几何模型可以将多元系还原为低元系。
下面证明在超额热力学函数的空间中偏差函数的对称性:
η(ij,ik)-η(ik,ij)
=0
(16)
偏差函数的对称性说明,新一代几何模型中,二元系的计算先后顺序对于模型的预报结果不会产生影响,新一代几何模型只有唯一的计算结果。这样使得计算过程中人为干扰因素得以去除,模型从而可以完全计算机化。
度量的第3条性质是三角不等式性质。这一点并不适用于偏差函数,这是由超额热力学函数的空间的性质决定的。因此对于一个i-j-k三元系,若要求
η(ij,jk)+η(ik,jk)≥η(ij,ik)
(17)
若式(17)成立,则由超额热力学函数的性质,上式等价于
[η(ji,jk)+η(ij,ji)+η(ki,kj)+η(ki,ik)+
η(jk,kj)]≥η(ij,ik)
(18)
由于超额热力学函数的空间中具有对称性,i-j二元系与j-i二元系是同一二元系,则
η(ij,ji)=0
(19)
这使得式(17)等同于
η(ji,jk)+η(ki,kj)≥η(ij,ik)
(20)
但这一不等式在超额热力学函数的空间中是不能成立的,仅需举出反例即可证明。
图3中给出了不同体系的二元系超额热力学性质函数之间的偏差函数η值,并以曲线表示。在图3a,b中,偏差函数η值并不能组成一个三角形。在图3c中则只有(12)-(23)-(24),(34)-(23)-(24)这两个三元系的偏差函数η值满足三角形不等式。因此以偏差函数η连结起来的二元系超额热力学函数的空间并不是一个简单的度量空间。这是由于超额热力学函数存在关于零点的镜像对称性造成的。这一空间的性质还需要进一步的数据收集和研究。因此偏差函数仅具有正定性与对称性,并不能作为超额热力学函数的空间的度量。

图3 不同熔体、溶液体系中二元系超额热力学函数之间的偏差函数η网络图: (a) Mg-Cu-Ni在1 173 K下的二元系超额吉布斯自由能[2],(b) 甲基氰+正庚烷+正辛烷在283.15 K下二元系超额摩尔体积[22], (c) 异丙醇(1)+甲基氰(2)+二氯甲烷(3)+正戊烷(4) 在 298.15 K下的二元系超额摩尔体积[23]Fig. 3 Network diagrams of deviaction function η among excess thermodynamic function of binaries in different melts and solution systems:(a) excess Gibbs free energies of binaries in Mg-Cu-Ni at 1 173 K[2],(b) excess molar volume functions of binaries in methyl butanoate-(n-heptane)-(n-octane)at 283.15 K[22],and (c) excess molar volume functions of binaries in propan-2-ol(1)+methyalacetate(2)+dichloromethane(3)+n-pentance(4) at 298.15 K[23]
6结论
(1) 由几何模型的计算特点出发,提出了二元系超额热力学函数空间的概念,这一空间中二元系超额热力学函数的关系以偏差函数表示。
(2) 通过与度量的定义进行对比,证明了新一代几何模型中偏差函数具有正定性与对称性。偏差函数的正定性使得几何模型可以将多元系向低元系还原,消除了对称几何模型的悖论。而偏差函数的对称性保证了几何模型可以完全计算机化,避免了非对称几何模型计算中的人为选择因素。
(3) 结果表明,由于二元系超额热力学函数空间本身的特性,使得偏差函数并不能作为超额热力学函数的度量,但偏差函数具有的正定性与对称性是新一代几何模型区别于传统几何模型的关键性质。
参考文献References
[1]Li Ruiqing(李瑞青),Chou Kuochih(周国治). NaCl-BaCl2-SrCl2三元熔盐相图的计算[J].ActaMetallurgicaSinica(金属学报),1989,25(3):B156-B161.
[2]Chou K C, Li W C, Li F S,etal. Formalism of New Ternary Model Expressed in Terms of Binary Regular-Solution Type Parameters[J].Calphad,1996, 20(4):395-406.
[4] Wang Xidong(王习东),Li Wenchao(李文超). 多元金属熔体黏度预报几何模型及分析比较[J].ScienceinChinaSeriesB(中国科学 B 辑),2003,33(2):164-171.
[5] Zhong X M, Liu Y H, Chou K C,etal. Estimating Ternary Viscosity Using the Thermodynamic Geometric Model[J].JournalofPhaseEquilib, 2003,24(1):7-11.
[6]Le Qichi(乐启炽),Zhang Xinjian(张新建),Cui Jianzhong(崔建忠),etal. 金属合金溶液热力学模型研究进展[J].ActaMetallurgicaSinica(金属学报),2003,39(1):35-42.
[7]Chen Zhiyuan, Liu Junhao, Yu Ziyou,etal. Electrical Conductivity of CaCl2-KCl-NaCl System at 1 080 K[J].ThermochimicaActa,2012,53(4):107-112.
[8]Hillert M. Empirical Methods of Predicting and Representing Thermodynamic Properties of Ternary Solution Phases[J].Calphad, 1980, 4(1): 1-12.
[9]Kohler F. Estimation of the Thermodynamic Data for a Ternary System from the Corresponding Binary Systems[J].MonatsheftefürChemie,1960,91:738-740.
[10]Muggianu Y, Gambino M, Bros J. A New Solution Model[J].JournalofChemicalPhysics,1965,72:83-88.
[11]Luck R, Gerling U, Predel B. On the Interpolation Algorithms for Thermodynamic Functions of Mixtures in Multicomponent Systems From Binary Boundary Systems[J].ZeitschriftfürMetaIlkunde,1986,77(7):442-448.
[12]Chou K C. A New Solution Model for Predicting Ternary Thermodynamic Properties[J].Calphad, 1987, 11(3): 293-300.
[13]Toop G. Predicting Ternary Activities Using Binary Data[J].TransactionsoftheMetallurgicalSocietyofAIME,1965,223:850-855.
[14]Chou K C, Austin C Y. A Study of Ternary Geometrical Models[J].BerichtederBunsengesellschaftfürPhysikalischeChemie,1989,93(6):735-741.
[15]Chou K C, Wei S K. A New Generation Solution Model for Predicting Thermodynamic Properties of a Multicomponent System from Binaries[J].MetallurgicalandMaterialsTransactionsB,1997,28(3):439-445.
[16]Zhang G H, Chou K C. General Formalism for New Generation Geometrical Model: Application to the Thermodynamics of Liquid Mixtures[J].JournalofSolutionChemistry,2010,39(8):1 200-1 212.
[18]Ma X, Yoshida F. Interaction Relation in 60Sn-Pb-0.05La Ternary Solder Alloy[J].MaterialsLetters,2002,56(4):441-445.
[19]Prasad L C, Mikula A. Surface Segregation and Surface Tension in Al-Sn-Zn Liquid Alloys[J].PhysicaB:CondensedMatter,2006,373(1):142-149.
[20]Wang L J, Chou K C. Seetharaman S. A Comparison of Traditional Geometrical Models and Mass Triangle Model in Calculating the Surface Tensions of Ternary Sulphide Melts[J].Calphad,2008,32(1):49-55.
[21]Gonz LEZ B, Calvar N, G Mez E,etal. Physical Properties of the Ternary System (Ethanol+Water+1-Butyl-3-Methylimidazolium Methylsulphate) and Its Binary Mixtures at Several Temperatures[J].JournalofChemicalThermodynamics,2008,40(8):1 274-1 281.
[22]Zhang G H, Chou K C. Estimating the Excess Molar Volume Using the New Generation Geometric Model[J].FluidPhaseEquilib, 2009, 286(1): 28-32.
[23]Zhang G H, Wang L J, Chou K C. A Comparison of Different Geometrical Models in Calculating Physicochemical Properties of Quaternary Systems[J].Calphad,2010,34(4):504-509.
[24]Iloukhani H, Khanlarzadeh K. Physicochemical Properties of Quaternary Systems and Comparison of Different Geometrical Models[J].JournalofChemicalandEngineeringData,2011,56(11):4244-4252.
[25]Zhen Qiang(甄强),Li Wengchao(李文超). 新一代几何模型 (周模型) 与对称和非对称模型的应用比较[J].ActaMetallurgicaSinica(金属学报),1999,35(7):748-750.
[26]Chen Zhuo(陈卓),Tao Dongping(陶东平). 几何模型应用于液态合金时体系对称性的一个热力学判据[J].NonferrousMetal(有色金属),2005,57(2):39-43.
[27]Hindler M, Mikula A. Calorimetric Investigations of Liquid Gold-Antimony-Tin Alloys[J].InternationalJournalofMaterialsResearch,2012,103(7):858-865.
[28]Chou K C. A General Solution Model for Predicting Ternary Thermodynamic Properties[J].Calphad,1995,19(3):315-325.
[29]Chou K C(周国治). 新一代的溶液几何模型及其今后的展望[J].ActaMetallurgicaSinica(金属学报),1997,33(2):126-132.
[30]Fan Peng(范鹏), Chou K C(周国治). 由组元的物性参数预测金属熔体的热力学性质[J].ActaMetallurgicaSinica(金属学报),1999,35(4):421-426.
[31]Qiao Z Y, Yan L J, Cao Z M,etal. Surface Tension Prediction of High-Temperature Melts[J].JournalofAlloysandCompounds,2001,325(1):180-189.
[32]Li Shou(林寿).TopologyofMetricSpacesandFunctionSpaces(度量空间与函数空间的拓扑)[M]. Beijing: Science Press,2004.
(编辑易毅刚)
第一作者:陈志远,男,1987年生,博士研究生
Properties of Similarity Coefficient in NewGeneration Geometric Model
CHEN Zhiyuan1,CHOU Kuochih1,2, WANG Lijun1,2, LI Fushen3
(1.State Key Laboratory of Advanced Metallurgy, University of Science and Technology Beijing, Beijing 100083, China)
(2.School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China)
(3.School of Materials Science Engineering, University of Science and Technology Beijing, Beijing 100083, China)
Abstract:With the development of the geometrical models, the new general solution model proposed by Chou has presented its advantages on the prediction of solution properties. Compendious calculation roadmap of geometrical models was given. In the present paper, comparisons between traditional geometrical models and new general solution model were performed by evaluating the properties of Sb-Ga molten alloy system and Cu2S-FeS-Ni3S2sulfur melting system. The calculation results showed the defects of symmetrical and asymmetrical models respectively, and also proved the self-consistency of the new generation model. Furthermore, from the viewpoint of mathematics, the key parameter of the new generational model, deviation function, was discussed by functional analysis. Positive definiteness and symmetrical characteristic of the deviation function of ternary properties were examined. The superiorities of the new general solution model were verified both in practical and theoretical aspects. Meanwhile, the current study also provided a new way to discuss the thermodynamics functions from the perspectives of functional analysis in mathematics.
Key words:thermodynamics; calculation of phase diagram; properties of solution; geometric models
中图分类号:TF801.2,O645.16
文献标识码:A
文章编号:1674-3962 (2015)05-0383-06
DOI:10.7502/j.issn.1674-3962.2015.05.10
通讯作者:王丽君,女,1979年生,副教授,Email:lijunwang@ ustb.edu.cn
基金项目:国家自然科学基金资助项目(51174022, 51104013); 科技部973计划项目(2012CB215405)
收稿日期:2014-04-21
