双平行四边形码垛机器人的运动学分析及功能研究
2015-02-24柳贺万君曾辉刘蕾
柳贺,万君,曾辉,刘蕾
(安徽埃夫特智能装备有限公司蔡鹤皋院士工作站,安徽芜湖 241009)
0 前言
随着现代工业的发展,重载搬码垛运机器人的应用越来越广泛,结构设计不同,对于机器人运动学算法也不同,但最终目的相同,大多设计成4自由度的串联机器人,有些针对该4自由度机器人应用D-H法进行运动学求解,计算量相对比较大。
文中以某公司生产的ER180机器人为研究对象,其结构由两组平行四边形组成。提出基于几何法的运动学分析方法,计算量小,便于实时控制,同时对运动算法进行仿真并实际应用,完全满足要求。
1 机器人模型与坐标系的建立
如图1所示,主平行四边形确定末端点位置,上臂的辅助平行四边形使末端执行器与水平面保持一个固定的姿态。驱动主平行四边形的电机被对称安装在转座上,其分别标为轴2、轴3,对应关节角度为θ2和θ3;转座由一个电机驱动,记为轴1,对应关节角度为θ1。前3个关节确定腕部末端点的位置,在手抓处加装一个电机,转角记为θ4,用以对所操作工件进行旋转。
坐标系如图2所示,其中全局坐标系为O0-x0y0z0,简记为O系。各个关节为1,2,3,4系,工具坐标系为T系。
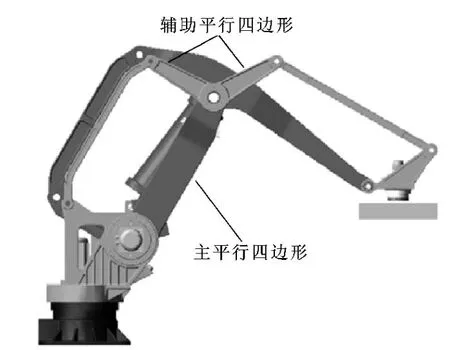
图1 机器人三维模型
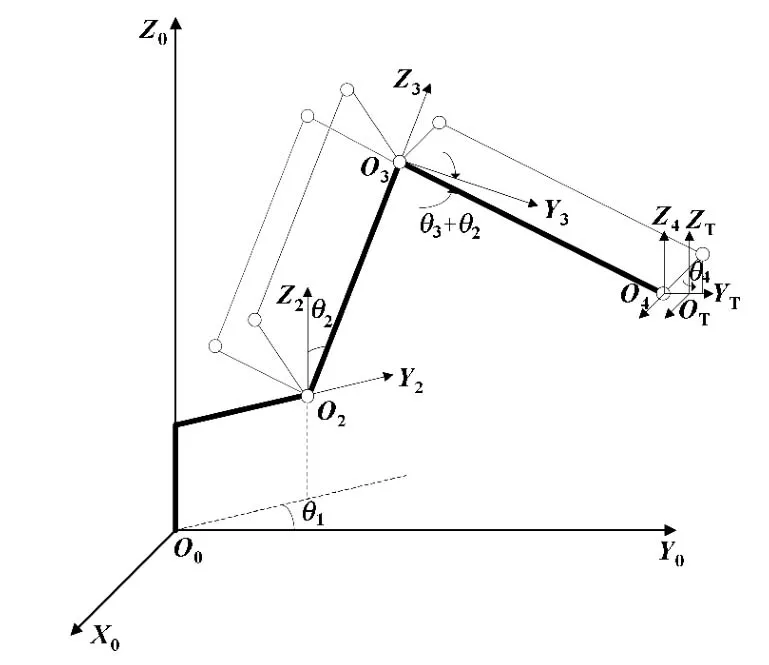
图2 机器人坐标系
2 机器人运动学正解
已知各个关节的转角,求得机器人工具端OT的姿态和位置,即为机器人的正解。用坐标变换来描述为从0到T的变换。从图2可知,从0到1的变换矩阵为1T0。依次类推2T1、3T2、4T3。从而可以得到从 0到4的坐标变换4T0。从0到T的变换为TT0=4T0TT4。即:

其中:TT4=Tz(θ4)+TR(yT,zT)
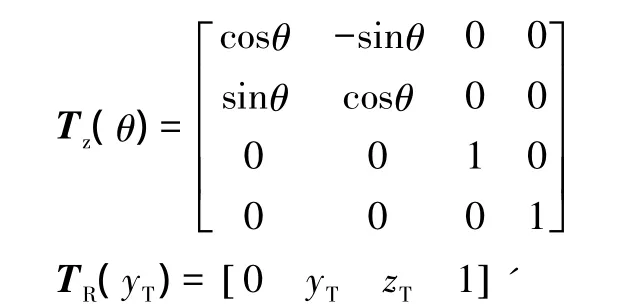
3 码垛机器人运动学求解
已知末端的位姿,求得各个关节的转角就是机器人的逆运动学求解。采用几何法进行求解,过程如下:
通过T系和变换TT4,可以求得腕部关节处4T0的变换矩阵。4T0=TT0(TT4)-1。利用这个关系可以求出小臂末端节点的位姿。

3.1 第一关节角θ1求解
参见图3,从几何关系中与双并联结构决定仅有1组解,即前腰 (Front)解:

其中:xp4,yp4,zp4为经过变换后的小臂末端节点处的位置。
3.2 第二关节角θ2求解
考虑θ1解的情况,参见图4,由此可得:
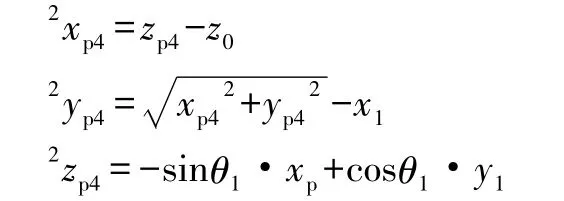
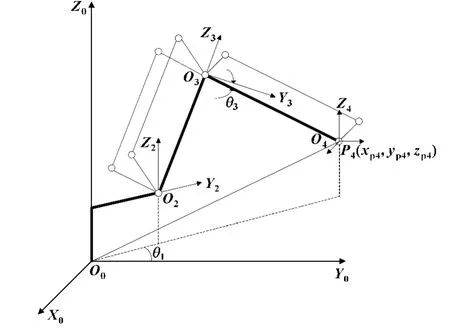
图3 第一关节角θ1计算

图4 第二关节角θ2计算
从图3可以看出:

其中:l1=O2O3;
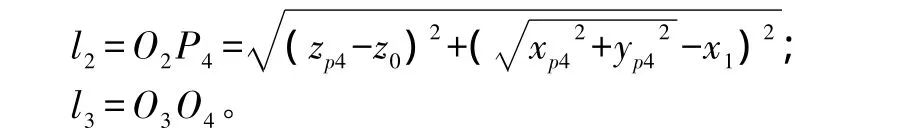
另一个角度θb为:

于是第二个关节角θ2为:

显然第二关节角只有1组解,即高臂 (Convex)解。
3.3 第三个关节角θ3求解
见图5,先求初始角度:

从而得到角度:


图5 第三关节角θ3计算
3.4 第四关节角θ4求解
关于旋转的解,则按式 (7):

其中:θz为码垛整体的绕T0坐标系的Z轴旋转角度。
由于双并联的结构决定运动学不存在多解情况,只存在前腰解和高臂解,所以不存在多组选解问题。
4 ER180机器人的运动控制验证
按照上述的算法封装成运动学库,分为:TRF_FOR正解与TRF_INV逆解,在每个插补周期,路径规划控制器调用运动库函数进行轴运动控制。机器人各部件与运动范围为:
z0=800,x1=350,l1=1 250,l3=1 400,yT=250,zT=225 θ1∈(-180,+180),θ2∈(-42,85),θ3∈(-120,20),θ4∈(-360,+360)
采用实际工程中的控制器离线仿真软件进行实际轨迹控制,轨迹为一圆弧,圆弧上3点的位姿为:
cp0:CARTPOS:=(x:=2000.15,y:=0.4,z:=1825.3,a:=0,mode:=0)
cp1:CARTPOS:=(x:=2600.15,y:= -599.6,z:=1525.7,a:=89.6,mode:=0)
cp2:CARTPOS:=(x:=2000.15,y:= -1199.6,z:=1825.3,a:=189.4,mode:=0)
cp0:CARTPOS:=(x:=2000.15,y:=0.4,z:=1825.3,a:=0,mode:=0)
测试TCP与各轴位移如图6—8所示。

图6 3D实际运行监视

图7 各关节运动位移图

图8 TCP的位姿图
由图7与图8可以看出,机器人在复杂的空间圆弧运动中,其位姿均大幅运动,能够平稳地实现平滑圆弧插补运动,表明了该四自由度机器人的运动学算法完善,可以达到期望的目标。
5 码垛功能的实现
码垛机器人主要用在搬运与码垛行业,这样码垛的功能显得尤为重要,主要实现过程一般示教起点与过渡点,设置码垛的参数 (包括码垛方式、层数、单层数量,间距等),机器人直接按照设置进行规划其他的码垛位置,拆跺为码垛的逆过程,码垛设置方式如图9所示。
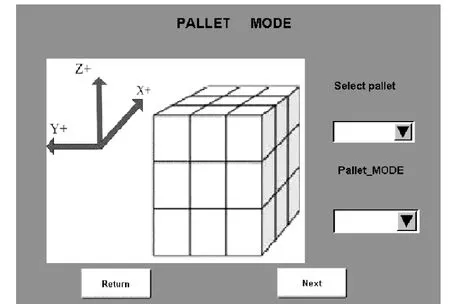
图9 码垛设置界面
但多数码垛的坐标系与机器人的直角不一样时,需要用到码垛用户坐标系OU,如图10所示。
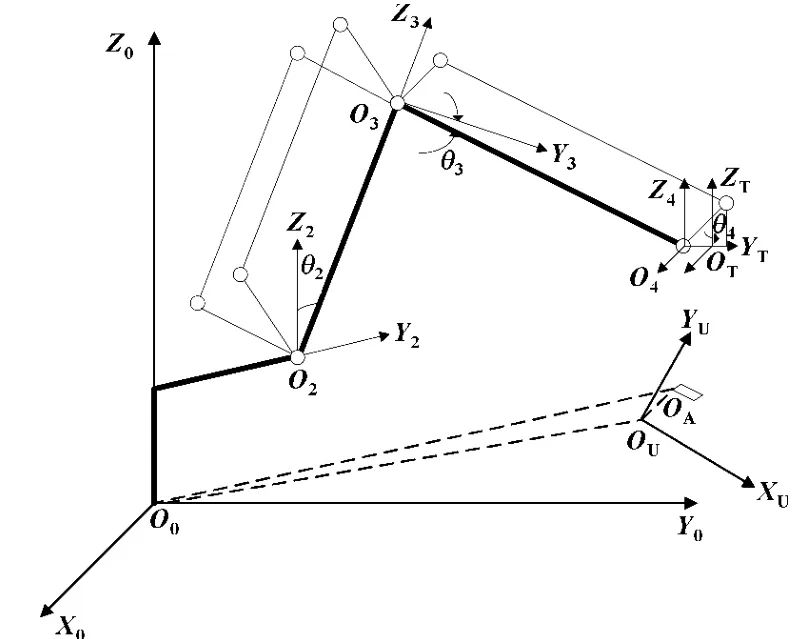
图10 码垛坐标系的转换
按照MT0=UT0*MTU可以将在码垛用户坐标系下的各码垛点位姿转化为机器人运动空间点,然后经过运动学库控制各轴按照规划曲线运动。
6 结论
在特殊结构的码垛机器人设计中,采用几何法进行运动学逆解运算,比一般的解析算法更加简单高效,便于实时控制;文中给出了四自由度双平行四边形码垛机器人的运动学算法,并实现了码垛与拆跺的功能设计,该算法已成功应用于公司生产的多款码垛机器人产品。
[1]刘鹏,宋涛,贠超,等.焊接机器人运动学分析及轨迹规划研究[J].机电工程,2013(4):390-394.
[2] SAEED B.Niku.Introduction to Robotics[M].BEIJING:Publishing House of Electronics Industry,2013.
[3]扶宇阳,葛阿萍.基于MATLAB的工业机器人运动学仿真研究[J].机械工程与自动化,2013(3):40-42.
[4]HUDYJAYA SiswoyoJo,NAZIM MirNasiri.Dynamic Modeling and Walk Simulation for a New Four-degree of-freedom Parallelogram Bipedal Robot with Sideways Stability Control[J].Mathematical and ComputerModelling,2013(1):25-28.
[5]苏学满,孙丽丽,杨明,等.基于Matlab的六自由度机器人运动特性分析[J].机械设计与制造,2013(1):78-80.
[6]谢斌,蔡自兴.基于MATLAB Robotics Toolbox的机器人学仿真实验教学[J].计算机教育,2010(19):140-143.
[7]张刚,黄海波.HP20机器人的运动学逆解计算及模拟仿真[J].轻工机械,2011,29(6):40-45.
[8]孙浩,赵玉刚,姜文革,等.码垛机器人结构设计与运动分析[J].制造业自化,2013(14):66-68.
[9]刘萍,陈莹.五自由度关节式机械手运动学分析及仿真[J].制造业自动化,2011(19):9-11.
[10]张普行,严军辉,贾秋玲.六自由度机械手的运动学分析[J].制造业自动化,2011(20):68-71
[11]MAYROGA R V,SANONGBOOM.A Radial Basis Function Network Approach for Geometrically Bounded Manipulator Inverse Kinematics Computation[C]//2003 IEEE/RSJ International Conference on Intelligent Robots and System,2003:3564-3569.
[12] DENAVIT J,HARTENBERG R S.A Kinematic Notation for Lower-pair Mechanisms Based on Matrices[J].ASM Journal of Applied Mechanics,1955,22(2):215-221.
[13]李成伟,朱秀丽,贠超.码垛机器人机构设计与控制系统研究[J].机电工程;2018,25(12):81-83.
