考虑驾驶员对线路熟悉程度的区域公交乘务排班模型*

孙　博　魏　明

(南通大学交通学院　江苏 南通 226019)



考虑驾驶员对线路熟悉程度的区域公交乘务排班模型*

孙博魏明▲

(南通大学交通学院江苏 南通 226019)

摘要在允许驾驶员跨线调度情形下，提出了一种考虑驾驶员对线路熟悉程度的区域公交乘务排班优化模型，满足驾驶员的工作时间窗、中途休息、用餐时间等现实因素，以最小化驾驶员成本、正常班及加班费用为目标函数，编制一个最佳公交乘务排班方案。根据问题特征，设计求解该问题的人工免疫算法，定义了抗体、启发式种群算法、适应度函数、免疫操作等。最后，结合算例分析，比较任意驾驶员对不同线路的偏好如何影响调度结果，仿真表明：随着驾驶员的熟悉线路程度增加，乘务排班的费用逐渐减少，虽然其调度成本比现有模型的高很多，但是该模型比较符合实际。

关键词交通管理；乘务员排班；多车场；驾驶员对线路的熟悉程度；人工免疫算法

0引言

在给定时刻表基础上，公交乘务排班(crew scheduling problem, CSP)主要解决在考虑工作制、中途休息及中午晚上用餐等因素，如何合理安排司机驾驶不同车辆去执行班次任务，是企业日常管理最关注工作之一，其方案的好坏直接决定了公交运营成本。CSP是一个NP难题[1]，在允许驾驶员跨线调度情形下，该问题可划分为单车场CSP(single depot crew scheduling problem，SDCSP)和多车场CSP(multiple depot crew scheduling problem，MDCSP)，考虑不同线路在各时段的发车不均衡性，后者比前者更容易节省运营成本，已经吸引了国内外众多专家学者、交通工程师的广泛关注。

目前， SDCSP的研究相对成熟[2-5]，MDCSP的研究相对较少，主要研究成果归纳如下：Gaffi和Nonato[6]采用近似算法首次研究一类多车场BCSP；陈明明等[7]建立了多车场乘务排班问题的数学模型；Huisman等[8]研究了多车场的车辆和人员集成调度模型；Leone等[9]提出一种融合领域搜索方法和路径构造方法的贪婪随机自适应搜索求解驾驶员排班问题；Marta等[10]设计求解混合公交车辆和驾驶员调度模型一种启发式算法；Christos和Efthymios[11]提出一种启发式算法求解混合公交车辆和驾驶员调度问题；沈吟东[12]研究探讨一类公交车辆和驾驶员的集成调度0-1整数规划模型；刘波涛和李会凯[13]研究一种基于免疫算法的公交车及驾驶员调度优化问题。由上可知，现有MDCSP研究均未涉及驾驶员在不同车辆之间切换，也没有考虑驾驶员对不同线路熟悉程度制约驾驶员执行相应班次，进而影响乘务排班结果，与实际应用有一定差距。

综上所述，笔者提出了一种考虑驾驶员对线路熟悉程度的公交乘务排班优化模型，设计求解该问题的人工免疫算法，在满足驾驶员的工作时间窗、用餐时间等实现约束情形下，编制了一个最佳公交乘务排班方案，并比较驾驶员偏好线路程度对调度方案的影响。

1问题描述及数学模型

综上所述，数学模型如下

(1)

st.Cp∩Cq=∅∀p,q∈D

(2)

(3)

(4)

(5)

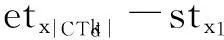
(6)

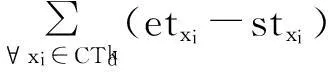
(7)

etxi-1+RT+zxi·ETstxi∀

(8)

在上述模型中，式(1)为问题的目标函数，表示公交乘务排班优化方案的营运成本极小化，包括总的驾驶员成本、正常班及加班费用；式(2)～(8)为问题的约束条件，其中：式(2)表示一个驾驶员仅属于一个车场，式(3)表示所有班次任务必须被驾驶员执行，式(4)表示每驾驶员同时只能完成一个班次任务，一个班次任务只能被一个驾驶员完成，式(5) 表示驾驶员仅执行熟悉线路的班次任务，式(6) 表示驾驶员的上班时间小于某值，式(7)表示驾驶员的在车时间低于某值，式(8)表示任意驾驶员按次序执行相邻班次任务的必备条件。

2求解SDCSP的人工免疫算法

人工免疫算法是借鉴自然免疫系统的一种智能算法，将抗原和抗体抽象为优化问题的目标函数与解，利用抗体的免疫操作机制快速收敛至全局最优解，在旅行商、物流配送、车间作业调度等组合优化领域已经广泛应用[14-15]。

目前，人工免疫算法在求解CSP方面尚不多见，本文设计求解SDCSP的人工免疫算法，根据问题特征，定义了抗体、启发式种群算法等，并描述了具体算法的求解流程。

2.1解的抗体表示

用向量X=(x1,x2,···,x|CT|)表示SDCSP的一个解，元素∀xi∈X为班次任务的编号(为1～|CT|之间的互不相同整数)，若遵循(8)式，班次任务xi-1和xi被某驾驶员按顺序执行；否则，它们被不同驾驶员完成，其中x1的前一个班次任务可能是x|CT|。显然，将X均解析为不同驾驶员的一系列班次任务序列，若它们满足约束式(5)～( 7)，它是一个可行解。

2.2产生抗体群

SDCSP涉及众多因素均是强约束的，随机产生的个体很难是可行解，设计启发式算法生成求解该问题的初始抗体种群。

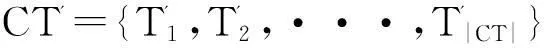
步骤2。令可执行CT'的驾驶员集合记为C=∅，设置i=1。

步骤3.1。设置uC=∅，对任意驾驶员∀k∈C，搜索他们的当前最后任务lT(k)。

2.3计算抗体适应值

值得注意的是，如果用红薯、白薯来替代主食，那么要额外增加一个蛋，或者几口鱼肉豆腐。因为甘薯的蛋白质含量低于大米和白面，如果长期吃甘薯而不搭配其他食物，则容易引起蛋白质缺乏。

抗体的适应度刻画候选解对最优解的贴近能力，可直接采用优化问题的目标函数变换得到，如下所示。

(9)

式中：C是常数，Qu是抗体u的适应度函数，f是该抗体映射问题的目标函数，C+f≥0。

2.4免疫操作

免疫进化操作的主要思想：计算抗体群的信息熵，据此选择较优的抗体，利用交叉和变异操作从中生成一些较好的抗体，维持抗体群的多样性。具体步骤描述如下：

步骤1。计算父代抗体群的每个抗体期望生存率pu，与抗体浓度Lu、适应值Qu相关。如式(10)所示，当抗体的Lu和Qu分别较低和较大时，其pu也越大，从而保护较好抗体和促进浓度较低个体进化，维持抗体群在进化中的多样性。

(10)

步骤2。根据式(10)，利用轮盘法，随机选择较好的抗体。

此外，引入免疫记忆细胞，将较好抗体直接保留到新群体中，避免其被舍弃。

2.5算法步骤

算法步骤见图1。

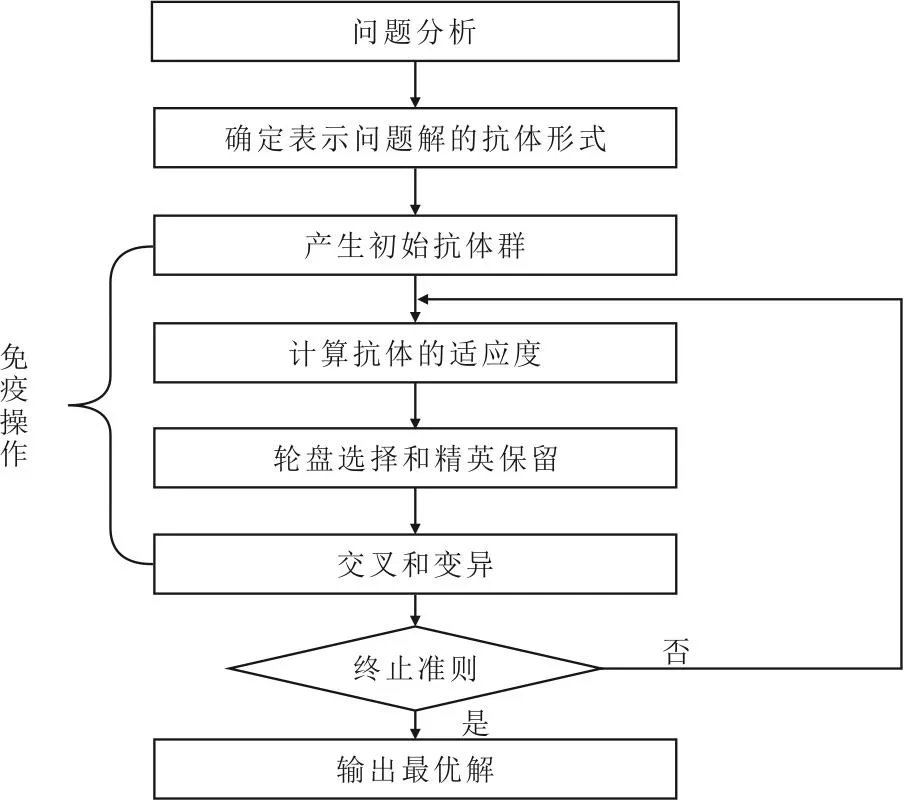
图1　基于人工免疫算法求解SDCSP的算法流程图Fig.1　Flowchart of SDCSP algorithm

3算例分析

某公交公司对6条线路进行区域乘务排班，共有3种类型驾驶员C1、C2和C3，其基本信息及所蕴含的时刻表如表1和2所示，其它运营参数为c1=126.4 元/人，c2=8.6 元/小时，c3=15 元/小时，RT=5 min，ET=15 min，LT=540 min和WT=480 min, 据此计算不同驾驶员熟悉线路情况下的最佳调度方案。

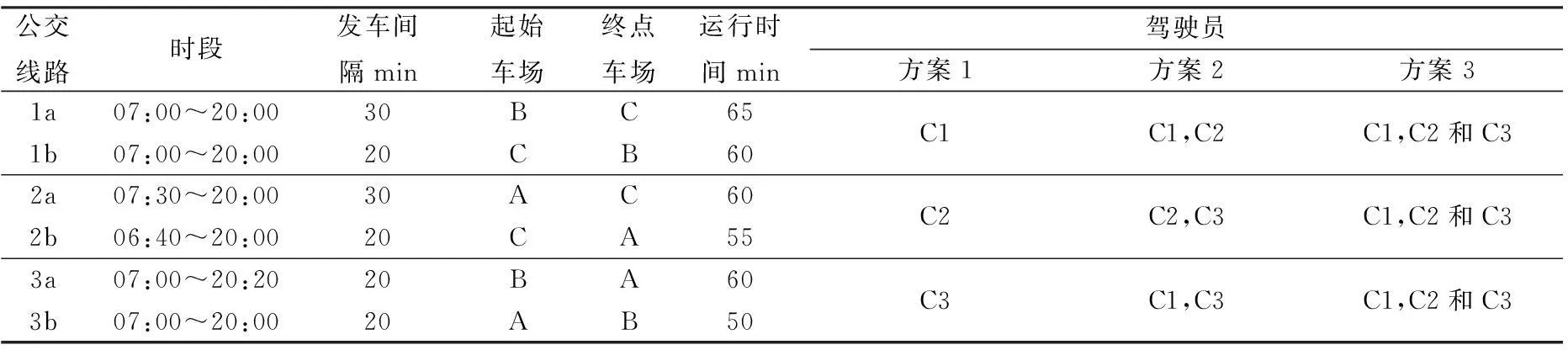
表1　公交线路信息

表2　行车时刻表

利用Matlab编写求解问题模型的免疫算法程序，设置相关参数为抗体数100，进化次数200，交叉率 0.2，变异率 0.02，淘汰率 0.2，浓度罚值 0.5，记忆细胞数30，计算3种驾驶员熟悉线路情况下的最佳调度方案，结果如表3所示，从中可知：随着驾驶员的熟悉线路数减少，需要更多的驾驶员，这引起他们的空闲时间增多和加班时间减少，由于人员费用的增加幅度大于加班费用的减少程度(正常班费用相差不大)，所以乘务排班的费用逐渐变大。由上可知，方案1和3分别是单和多车场CSP，而方案2是多车场CSP的改进模型，虽然其调度成本比现有多车场CSP的高很多，但是该模型比较符合实际。

表3　不同方案的计算结果分析

方案2的最佳调度方案如表4所示，总共需要40个驾驶员花费8 013.9元才能完成215个班次，3类驾驶员C1，C2和C3的数量分别为13，14和13，所有乘务员在3个车场A，B和C的初始分布数量为3，5 和32，他们的总工作、空闲和加班时间分别为7 985 min、4 705 min和12 430 min。由于各线路的发车频率不均衡性，考虑驾驶员对各条线路的熟悉程度偏好，可能出现部分驾驶员仅执行一个或少数班次任务，计算结果符合直观分析。

表4　最佳驾驶员排班方案

4结论

遵从“一车多司机”制，与单线公交乘务排班相比，区域调度模式可以有效减少运营成本。然而，若该调度模式忽略驾驶员对不同线路的熟悉程度，不仅影响调度成本，而且容易造成交通隐患。针对现有研究较少关注此类问题，文中研究一类考虑驾驶员对线路熟悉程度的区域公交乘务排班优化模型及其求解算法，在满足驾驶员的工作时间窗、用餐时间、加班费用等现实约束情形下，合理安排驾驶员完成一系列班次任务。仿真表明：随着驾驶员的熟悉线路程度增加，乘务排班的费用逐渐减少，虽然其调度成本比现有模型的高很多，但是该模型比较符合实际。

然而文中模型未考虑不确定因素对乘务排班的影响，当交通拥堵等随机干扰引起车辆延误完成某个班次，这容易导致当前乘务排班方案失效，故亟待寻求编制一个高可靠、低成本的乘务排班方案以适应不断变化环境，将是今后进一步研究的方向。

参考文献

[1]CEDER A. Public Transit Planning and Operation Theory,Modeling and Practicce[M].Atlanta, USA:Elsevier，2007.

[2]LOURENCO H R, PAIXAO J P, PORTUGALL R. Multiobjective metaheuristics for the bus-driver scheduling problem[J]. Transportation Science, 2001, 35(3): 331-343.

[3]沈吟东,倪郁东. 含时间窗的司售员调度模型及多邻域结构设计[J]. 华中科技大学学报：自然科学版, 2008,36 (12):31-34.

SHEN Yindong, NI Yudong. Model for crew scheduling with time windows and multi-neighborhood structure[J]. Journal of Huazhong University of Science and Technology：Natural Science Edition, 2008,36(12):31-34.

[4]CHEN Mingming, NIU Huimin. A model for bus crew scheduling problem with multiple duty types[J]. Discrete Dynamics in Nature and Society, 2012, 2012(2):407-432.

[5]FRELING R, HUISMAN D, WAGELMANS A. Models and algorithms for integration of vehicle and crew scheduling[J].Journal of Scheduling, 2003,6(1), 63-85.

[6]GAFFI A, NONATO M.Computer-aided transit scheduling[M]. Berlin:,Springer-Verlag, 1999.

[7]陈明明,牛惠民. 多车场公交乘务排班问题优化[J]. 交通运输系统工程与信息, 2013, 13(5): 159-166.

CHEN Mingming，NIU Huimin. An optimization model for bus crew scheduling with multiple depots[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(5): 159-166.

[8]HUISMAN D, FRELING R, WAGELMANS A. Multipledepot integrated vehicle and crew scheduling[R].Washington D.C. USA:Economic Institute, 2003.

[9]LEONE R, FESTA P, MARCHITTO E. Solving a bus driver scheduling problem with randomized multistart heuristics[J]. International Transactions in Operational Research, 2011,18(6): 707-727.

[10]MARTA M, MARGARIDA M, ANA P. A decomposition approach for the integrated vehicle-crew-roster problem with days-off pattern[J]. European Journal of Operational Research, 2013, 229(2): 318-331.

[11]CHRISTOS V, EFTHYMIOS H. Combined bus and driver scheduling[J]. Computers and Operations Research, 2002, 29(3):243-259.

[12]SHEN Y, XIA J. Integrated bus transit scheduling for the Beijing bus group based on a unified mode of operation[J]. International Transactions in Operational Research, 2009, 16(2):227-242.

[13]刘波涛,李会凯.公交车和驾驶员集成调度算法研究[J].计算机工程与科学, 2011,33(4):150-153.

LIU Botao, LI Huikai. Research on the scheduling algorithm of city buses and drivers[J]. Computer Engineering& Science, 2011,33(4):150-153.

[14]王 冰,李巧云,尹 磊.基于人工免疫算法的鲁棒满意项目调度[J].计算机集成制造系统,2011,17(5): 1089-1094.

WANG Bing, LI Qiaoyun, YIN Lei. Robustsatisfying project scheduling based on artificial immune algorithm[J].Computer Integrated Manufacturing Systems,2011,17(5): 1089-1094.

[15]KIM J W. Integrating artificial immune algorithms for intrusion detection[D]. London: University College London, 2002.

An Optimization Model for Regional Crew Scheduling

Problem Considering the Driver′s Familiarity to Bus Lines

Bo SunWei Ming▲

(SchoolofTransportation,NantongUniversity,Nantong226019,Jiangsu,China)

Abstract：In the case of allowing drivers to cover tasks belonged to different bus lines, a model for regional crew scheduling is proposed by considering each driver′s familiarity to different bus lines. The model meets the following constraints such as working time, halfway rest, and mealtime. The objective is to identify the best crew scheme to minimize operating costs, and salary costs of bus drivers by taking regular and overtime work into consideration. The solutions are obtained using a tailored artificial immune algorithm which redesigned a solution code, heuristic procedure to initialize chromosomes randomly, fitness function, immune operation, etc. Finally, a numerical example is presented to calculate the best scheme and the impacts of drivers' preference for different lines on the scheduling scheme, which in turn demonstrates the effectiveness of the model and algorithm. Simulation results show that the costs of crew scheduling decrease with the increasing drivers′ familiarity with one bus line. Although its scheduling cost of proposed model is much higher than the existing models, the one proposed in this paper is more realistic.

Key words：traffic management; crew scheduling; multiple depots; driver′s familiarity with different bus lines; artificial immune algorithm

通信作者：▲魏明(1984-)，博士.研究方向：公交调度.E-mail: mingtian911@163.com

作者简介：第一孙博(1986-)，硕士.研究方向：交通规划与管理.E-mail: bowensunny@163.com

基金项目*国家自然科学(批准号：61503201)、中国博士后科学基金面上项目(批准号：2013M540408)、江苏省高校自然科学研究面上项目(批准号：13KJB580008，15KJB580011)、南通科技计划项目(批准号：BK2014059)资助

收稿日期：2015-09-25修回日期：2015-11-23

中图分类号：U491

文献标志码：A

doi：10.3963/j.issn 1674-4861.2015.06.020