侧风对桥面车辆转弯安全性的影响分析*
2015-02-24蔡晓男陈圣迪蒋愚明
蔡晓男 陈圣迪 蒋愚明 陆 键,
(1.上海交通大学船舶海洋与建筑工程学院 上海 200240;
2.上海海事大学交通运输学院 上海 201306;3.同济大学交通运输工程学院 上海 200092)
侧风对桥面车辆转弯安全性的影响分析*
蔡晓男1陈圣迪2▲蒋愚明3陆键1, 3
(1.上海交通大学船舶海洋与建筑工程学院上海 200240;
2.上海海事大学交通运输学院上海 201306;3.同济大学交通运输工程学院上海 200092)
摘要针对桥面弯道处车辆的受力状况,综合考虑车辆类型、道路条件、车速和风速的影响,建立安全行车的极限平衡方程。在此基础上,结合某斜拉桥相关数据,计算不同车速下安全行车的临界风速,结果表明,安全行车临界风速随车速的增加先增加后减小,这一变化与通常认为的车速越大临界风速越小相违背。为验证悖论现象是否合理,论文研究了车速和临界风速的变化关系,并结合具体案例计算悖论现象发生时的车速分布区间,以全面理解侧风对桥面安全行车的不同影响,保障桥梁的安全运营。
关键词交通工程;临界风速;极限平衡方程;桥面侧风;行车安全
0引言
近几年,我国的大跨度桥梁建设取得了骄人的成绩,例如,杭州湾跨海大桥、苏通长江公路大桥。大跨度桥梁运营过程中常遇到以下几个问题[1]:①同一风场中,桥位风速要比气象站的实测地面风速高出很多;②桥面周围遮挡物较少,桥塔区域局部风场变化剧烈。大跨度桥梁多位于我国东部沿海地区,瞬时强风、台风天气频发,所以桥上行车面临着极大的安全隐患。以苏通大桥为例,2009年桥面7级以上风力的天数约有179 d,再加上雨、雪、冰、雾等其他因素的共同作用,大大增加了交通事故发生的可能及严重程度。
根据车辆行驶方向和风向之间的关系,可将风分为顺风、逆风和侧风。研究表明,当遭受突发侧向阵风作用时,车辆最容易发生事故[2]。一般认为,由风引发的车辆事故包括侧翻、侧偏和侧滑。Baker[3]研究了这3种事故的判定标准,在车辆突然受到侧风作用的0.5 s内,若车辆迎风侧的任一车轮与路面的竖向接触力为0,则发生侧翻事故;若车辆偏转位移超过0.2 rad,则发生偏转事故;若车辆侧向位移超过0.5 m,则发生侧滑事故。风致车辆事故,轻则车辆破坏,财产损失,重则人员伤亡,甚至会威胁桥梁结构的安全。并且这类事故会干扰邻近车道的正常运行,容易诱发严重的二次事故。为预防和减少此类事故发生,不仅需要工程防护措施[4-5],更需要研究不同条件下车速和风速之间关系,制定科学的车速控制标准,保障桥上行车安全畅通。
研究表明,桥面侧风导致的车辆事故中,侧滑是最主要的问题[6]。很多桥面车速和风速关系的研究都是以不发生侧滑为条件建立模型。这里的风速是指车辆以任一车速行驶不发生侧滑的临界风速,也称安全行车临界风速或安全行车标准风速。分析桥面车速和临界风速关系的模型主要有2种:①根据侧风影响下车辆转弯时的行驶状态,建立力学平衡方程,计算车速与临界风速之间的关系[4,7-8],在此基础上,也可以结合风速风向的概率分布,计算安全行车的概率[5-6]。②将风、车辆、桥梁作为整体,建立风-车-桥耦合系统模型,分析系统的振动特性[9-10],计算不同条件下的临界风速[2]。这些研究为车速的科学管理提供了依据,提高了大桥的安全运营水平。
实际工程中,笔者根据车辆转弯时的极限行驶状态,建立力学平衡方程,计算不同车速对应的安全行车临界风速。在对临界风速分析的过程中,发现了一个有趣的现象,在车速的某个范围内,临界风速随着车速的增加而增加。也就是说,临界风速是随着车速的增加先增加后减小。这与以往的研究(临界风速随着车速的增加而减小)不完全一致。以往的研究中,车速的计算间隔设置较大,使得这一现象未被重视。而笔者分析了这一现象(下称,悖论现象)是否合理,若合理,计算悖论现象对应的车速分布区间,以全面理解侧风对桥面安全行车的影响,明确车速与临界风速之间的变化关系。
1侧风作用下车辆的安全行驶条件
桥面侧风导致的车辆事故中,侧滑是最主要的问题[6]。当车辆在桥面行驶时,弯道处因受离心力作用,车辆的稳定性和安全性较差。所以,综合考虑风力、离心力、重力的共同作用,以不发生侧滑为安全行驶条件,建立桥面车辆转弯的力学模型[11]。见图 1。

图1 车辆转弯处受力分析Fig.1 Force analysis of a turning vehicle
如图1所示,风速Vw与车速Vc垂直,为保证车辆不发生侧滑,必须满足车辆转弯时的离心力F,侧风侧向力FS,以及重力水平分力Gs之和不大于侧滑极限力Ff,即
(1)
式中:m为汽车质量;R为车辆转弯半径;Cs为侧向气动系数;ρ为空气密度;V为绝对速度,车速、风速的矢量和;A为车辆的正投影面积; g为重力加速度;α为转弯处路拱横坡;μS为路面摩擦系数;FL为侧风提升力;CL为升力系数。整理得:
(2)
显然不等式(2)为侧风作用下车辆安全行驶(不发生侧滑)的必要条件,当不等式取等号时,即为安全行车的极限平衡方程。需要注意的是,不等式中Cs和CL的确定比较困难,根据文献[12-14]风洞试验的结果,侧向气动系数Cs和升力系数CL与风向角β之间基本满足正比例关系[6]。
Cs=kcs·β和CL=kcL·β
(3)
式中:β为车速与风速的夹角;kcs和kCL为比例系数。因此,得到车辆转弯时刚好不发生滑移的极限平衡方程。
(4)
2安全行车临界风速计算
安全行车临界风速是指车辆以不发生滑移满足极限平衡方程为条件,任一车速对应的风速值。其主要用于桥梁日常运营的车速管理,对保障车辆安全通行,预防和减少风致车辆事故有重要意义。
2.1桥梁参数
参考某斜拉桥的相关数据,车辆转弯半径为2 000 m,桥面附近空气密度为1.293 g/L,转弯处路拱横坡度为1.4%,考虑到该斜拉桥地处北亚热带南部湿润季风气候,温度较高,冰冻现象不多见,但降雨频繁,多雾,空气湿度大,路面摩擦系数取0.5。
2.2车型参数
不同车型的质量、正投影面积、行驶动力性和稳定性存在较大差异。车型参数的差异会影响空气动力学相关参数,直接决定着侧风侧向力与上升力的变化。目前对于车型的划分主要有2种:轿车和卡车或者轿车、微型客车、中型客车和集装箱挂车。这里采用文献[15]的相关数据。
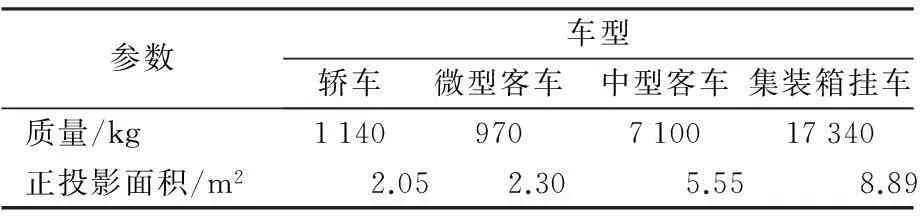
表1 不同车型参数
2.3Cs和CL
只要依据不同车型确定合理kcs和kcL,就能确定Cs和CL。这里采用文献[4]的研究数据。
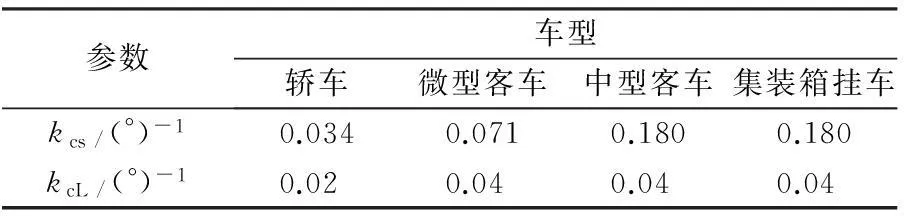
表2 不同车型的kcs和kcL参数
2.4安全行车临界风速计算
将不同车型的质量、正投影面积、kcs和kcL带入安全行车的极限平衡方程,利用Matlab的fsolve函数,计算车速在20~100 km/h时对应的安全行车临界风速。根据计算结果,绘制4种车型车速与临界风速之间的关系,见图2。

图2 车速与临界风速之间的关系Fig.2 Relationships between vehicle speed and critical wind speed
由图2知:
1)不同车型,在相同车速条件下有着不同的临界风速值,并且微型客车<中型客车<集装箱挂车<轿车,因为轿车正投影面积小,侧风侧向力小,质量小,集装箱挂车正投影面积大,侧风侧向力大,质量大,所以它们的临界风速较大,对侧风不敏感;而微型客车和中型客车有较大的正投影面积,较大的侧风侧向力,较小的质量,故它们的临界风速较小,对侧风敏感。
2)同一车型,临界风速并不是随着车速增加一直减小,而是先有微小增加后逐渐减小,这一变化与通常认为的,车速越大临界风速越小相违背。下面将对这一悖论现象进行分析,研究其是否合理。
3悖论现象分析
在证明悖论现象是否合理前,先分析式(4)极限平衡方程中,临界风速和车速的变化对不同作用力的影响。
1)车辆转弯的离心力F,仅与车速的二次方成正比。
2)重力包括水平和竖向分力,当给定路拱横坡时,两者数值保持不变,与车速风速的变化无关。

另一方面,根据极限平衡方程,可将ε化简为
(5)



图3 车速Vc,风速Vw和ε之间的关系Fig.3 Relationships of vehicle speed Vc, wind speed Vw, andε
4车速分布区间计算
至此已证明,安全行车临界风速随着车速的增加可能出现先微小增加后逐渐减小的变化趋势。但更重要的是确定在什么情况下,尤其是车速在什么范围内,这一现象才会发生。显然,安全行车极限平衡方程(4)是关于车速和风速的隐函数,不可能得到车速的具体表达式,但在给定参数条件下,利用一些隐函数求解算法,可以求出某个具体案例当悖论现象发生时车速的分布区间。


表3 悖论现象发生时不同车型的车速分布区间
5结束语

参考文献
[1]陈晓冬.大跨桥梁侧风行车安全分析[D].上海:同济大学,2007.
CHEN Xiaodong. Analysis of vehicle safety under cross wind on long span bridges [D]. Shanghai:Tongji University, 2007. (in Chinese)
[2]韩万水,陈艾荣.风环境下行驶于大跨度桥梁上的车辆安全评价及影响因素研究[J].空气动力学学报,2008,26(4):466-472.
HAN Wanshui, CHEN Airong. Safety assessment of moving vehicles on a long-span bridge under crosswind and influence factors analysis [J]. Acta Aerodynamica Sinica, 2008,26(4):466-472. (in Chinese)
[3]BAKER C. J. A simplified analysis of various types of wind-induced road vehicle accidents[J]. Journal of Wind Engineering and Industrial Aerodynamics,1986, 22(1): 69-85.
[4]陈艾荣,王达磊,庞加斌.跨海长桥风致行车安全研究[J].桥梁建设,2006,(3):1-4.
CHEN Airong, WANG Dalei, PANG Jiabin. Study of wind related riding safety on long sea crossing bridge [J]. Bridge Construction, 2006,(3):1-4. (in Chinese)
[5]韩万水,马 麟,院素静,等. 基于风速风向联合分布的桥面侧风所致车辆事故概率性分析[J]. 中国公路学报,2010,23(2):43-49.
HAN Wanshui, MA Lin, YUAN Sujing, et al. Probability analysis of bridge deck side wind-induced vehicle accidents based on joint distribution of wind speed and wind direction [J].China Journal of Highway and Transport, 2010,23(2):43-49. (in Chinese)
[6]庞加斌,王达磊,陈艾荣,林志兴.桥面侧风对行车安全性影响的概率评价方法[J]. 中国公路学报,2006,19(4):59-64.
PANG Jiabin, WANG Dalei, CHEN Airong, et al. Probability evaluating method of bridge deck side wind effects on driving safety [J]. China Journal of Highway and Transport, 2006,19(4):59-64. (in Chinese)
[7]江 浩,余卓平.风力对跨海大桥上行驶车辆安全性的影响分析[J].同济大学学报:自然科学版,2002,30(3):326-330.
JIANG Hao, YU Zhuoping. Effect of high winds on driving safety of vehicles on long span bridges at sea [J]. Journal of Tongji University:Natural Science Edition, 2002,30(3):326-330. (in Chinese)
[8]于群力,陈徐均,江召兵,等.不发生侧滑为指标的跨海大桥安全行车风速分析[J].解放军理工大学学报:自然科学版,2008,9(4):373-377.
YU Qunli, CHEN Xujun, JIANG Shaobing, et al. Analysis of safety wind velocity of driving on sea-cross bridge based on target of no sideslip [J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2008,9(4):373-377. (in Chinese)
[9]韩万水,马 麟,刘健新.引入驾驶员行为的风-汽车-桥系统耦合振动研究[J]. 中国公路学报,2011,24(1):42-49.
HAN Wanshui, MA Lin, LIU Jianxin. Research on coupling vibration of wind-vehicle-bridge system with considering driver behavior [J]. China Journal of Highway and Transport, 2011,24(1):42-49. (in Chinese)
[10]李永乐,赵 凯,吴梦雪,等. 斜独塔混合梁斜拉桥风-汽车-桥梁系统耦合振动研究[J]. 中国公路学报,2012,25(1):47-54.
LI Yongle, ZHAO Kai, WU Mengxue, et al.Study of coupling vibration of wind-vehicle-bridge system for inclined single pylon cable-stayed bridge with hybrid girder [J]. China Journal of Highway and Transport, 2012,25(1):47-54. (in Chinese)
[11]威鲁麦特 H P.车辆动力学 [M]. 孙逢春,译.北京: 北京理工大学出版社, 1998.
WILLUMERT H P. Vehicle dynamics [M]. Translator:SUN Fengchun.Beijing: Beijing Institute of Technology Press, 1998. (in Chinese)
[12]Society of Automotive Engineers, Inc. Aerodynamic testing of road vehicles: Testing methods and procedures[R]. Detroit, USA:Road Vehicle Aerodynamics Forum Committee,1991.
[13]同济大学土木工程防灾国家重点实验室.TJ-2汽车模型风洞测试报告[R].上海:同济大学, 1988.
The State Key Laboratory for Disaster Reduction in Civil Engineering of Tongji University. Testing report of TJ-2 automotive model wind tunnel [R]. Shanghai:Tongji University, 1998. (in Chinese)
[14]黄向东.汽车空气动力学与车身造型[M].北京:人民交通出版社,1999.
HUANG Xiangdong. Automotive aerodynamics and vehicle style [M]. Beijing: China Communications Press, 1999. (in Chinese)
[15]中国汽车工业总公司,中国汽车技术研究中心.中国汽车车型手册[M].济南:山东科学技术出版社,1993.
China Automotive Industrial Company, China Automobile Technology and Research Center. China automodel manual [M]. Jinan: Shangdong Science and Teachnology Press, 1993. (in Chinese)
The Effects of Side Wind on the Safety of Turning Vehicles on Bridges
CAI Xiaonan1CHEN Shengdi2▲JIANG Yuming3LU Jian1, 3
(1.TransportationResearchCenter,ShanghaiJiaoTongUniversity,Shanghai200240,China;
2.CollegeofTransportationandCommunications,ShanghaiMaritimeUniversity,Shanghai201306,China;
3.CollegeofTransportationEngineering,TongjiUniversity,Shanghai200092,China)
Abstract:In order to analyze the effects of side wind on the safety of vehicles traveling on the curve sections of bridges, under the combined effects of vehicle types, road conditions, vehicle speed and wind speed, the force applied to vehicles are studied to develop a limit equilibrium equation. According to the observed data from a cable-stayed bridge in China, critical wind speed is calculated at various vehicle speeds for maintaining a safe vehicle operation. Results show that as vehicle speed increases, critical wind speed increases slightly within a certain range, then descends. Such result contrasts to previous studies which commonly believe that critical wind speed decreases with increasing vehicle speed. To further study this paradox, the relationship between vehicle speed and critical wind speed is analyzed, and the distribution range of the corresponding vehicle speed is calculated when the above paradox occurs. The conclusions from this study are helpful for presenting a comprehensive understanding of the effects of side wind on vehicle safety, and to maintain a safe operation of the bridges.
Key words:traffic engineering; critical wind speed; limit equilibrium equation; side wind; driving safety
通信作者:▲陈圣迪(1985-),讲师.研究方向:交通安全,风险管理.E-mail: sdchen@shmtu.edu.cn
作者简介:第一蔡晓男(1988-),博士研究生.研究方向:交通安全,交通仿真,风险评估与管理.E-mail: heyman@sjtu.edu.cn
基金项目*广东省交通运输厅科技立项项目(批准号:2011-01-002)、国家自然科学(批准号:50908146)资助
收稿日期:2015-10-01修回日期:2015-11-11
中图分类号:U491
文献标志码:A
doi:10.3963/j.issn 1674-4861.2015.06.012
