交通事件持续时间预测的贝叶斯网络模型*

马雪婧　邵春福▲　钱剑培　王天倚

(1. 北京交通大学城市交通复杂系统理论与技术教育部重点实验室　北京 100044；

2.南通恒龙信息科技有限公司　江苏 南通 226000)



交通事件持续时间预测的贝叶斯网络模型*

马雪婧1邵春福1▲钱剑培1王天倚2

(1. 北京交通大学城市交通复杂系统理论与技术教育部重点实验室北京 100044；

2.南通恒龙信息科技有限公司江苏 南通 226000)

摘要交通事件是引发道路交通拥堵的主要因素之一，通过实时交通诱导等手段可以降低其对交通运行造成的影响，而及时准确地预测事件持续时间则是实现有效管控的前提条件。基于MIT打分函数，融合自上而下的网络生长规则，引入蚁群算法寻找最优网络结构，即以S-ACOB算法为核心搭建最优贝叶斯网络模型。增加了节点随机选择机制及局部结构概率选择模式，降低局部最优结果生成概率，确保贝叶斯网络的健壮性。通过实例验证及对比分析，针对观测节点属性完备和缺失的情况，网络模型预测精度分别为76.97%和93.23%，平均预测精度可达87.82%，证明该模型可以有效地预测交通事件持续时间。

关键词交通工程；交通事件；持续时间预测；贝叶斯网络；结构学习；MIT算法；S-ACOB算法

0引言

据公安部交通管理局统计，2013年全国共接报道路交通事故598.7万起。由于交通事件的处理需要报警或发现、响应、清除等步骤，有必要准确预测交通事件持续时间，并及时进行交通管控、交通诱导，提出出行信息服务。Golob等[1-3]在预测交通事件持续时间方面进行了大量早期研究，提出了各种预测方法，主要有：概率分布、回归分析、风险模型、决策树和时间序列模型等。由于数据源、样本量，以及采用的方法和模型等差异，有学者提出了一些利用缺失数据进行预测的非参数方法[4-6]，其中，贝叶斯网络预测效果显著，不断有学者对该方法进行研究和实证检验。

Sami Demiroluk等[7]根据利用K2算法对交通事件持续时间进行预测，最高预测精度提高22%；李大韦[8]通过推理算法构建了一般贝叶斯网络模型，在数据缺失不超过30%情况下，模型30 min预测准确率超过80%；张良力等[9]运用簇树推理算法构建贝叶斯网络模型对驾驶行为进行分析与预测；杨超等[10]利用BNT工具箱实现结构学习与参数学习，得到的最大绝对误差为10.32%；通过前人的研究成果可以看出，以贝叶斯网络进行预测是可行的。但大多数研究者采用K2算法或数据挖掘平台进行预测，具有一定的局限性，在一些情况下不能提供适合当前数据集的网络结构，且算法的搜索效率不高；为降低计算复杂度，部分论文对不显著的事件属性节点进行删减，虽然可以减少结构搜索时间，但是在一定程度上降低了模型的可信度。故而有必要在数据集的基础上，研究网络模型搭建方法。笔者结合了属性节点间互信息量与条件独立性测试、局部结构搜索、结构空间搭建、评分寻优搜索等方法，构建了以S-ACOB算法为核心的贝叶斯网络模型。采用自上而下的网络生长模式，随机选择初始节点及后续生长节点以增强网络结构的多样性；根据网络生长规则搜索合理的局部结构，确保模型的准确性；一次性确定网络结构的边及方向，避免二次搜索，大大提高搜索效率。

1贝叶斯网络结构学习

贝叶斯网络是一种有向图模型，借助有向无环图，图像化变量之间的相互关系，得到节点处的条件概率分配。采用评分-搜索方法，以打分函数g(G:D)作为判断标准，构建最符合数据集D的网络结构。常用算法有LL评分，MDL评分，BIC评分，AIC评分，NML，MIT等。

笔者采用MIT评分准则，该评分使用子节点与父节点之间的互信息和独立性测试评估两者的相关程度来构造贝叶斯网。该算法学习效率较好，贴合贝叶斯网络的语义，更大程度的还原数据本来面目，增强模型的真实性。

MIT全局打分函数为[8]

gMIT(G:D)=

(1)

式中：N为样本容量；Pa(Xi)为变量Xi的父节点集；ID(Xi,Pa(Xi))为Xi与Pa(Xi)的互信息；χα,liσi(j)为卡方检验值。

因Pa(Xi)中各变量的分类数ri会影响自由度lij的计算，将Pa(Xi)中变量依据ri的大小排序，得到变化后Xi的父节点集为Paσi(j)。式(1)中，前一项主要计算点Xi与其父节点集Pa(Xi)的互信息，后一项将独立性检验作为罚项。式(2)计算了在Paσi(j)情况下，卡方检验自由度liσi(j)。其中：riσi(j)为排序后的父节点集Paσi(j)的分类数。

对于节点集合I={X1,…,Xn}，其联合概率P可以由式(3)表示。

(3)

2S-ACOB算法

ACOB算法[5]是基于蚁群寻优的得分搜索算法，使用贪心算法进行局部优化，但这种方法时间复杂度较高。因此一些学者提出I-ACOB算法[6]，通过条件独立性测试去掉无关联的边，并利用ACOB方法在缩小的解集寻找最优网络结构，但只测试节点间是否独立，未考虑局部网路结构与各节点的独立关系，如此缩小解集范围容易造成搜索空间的不完整。笔者所提出S-ACOB的主要目标是在保障模型准确性的基础上降低运算时间，其具体的实现思路是在ACOB的基础上，通过MIT局部打分函数，判断局部网络结构与后续生长节点之间的独立关系，以得到最优网络结构。

2.1S-ACOB的参数及规则

1) 信息素τ。当某只蚂蚁找到了评分最大的结构，该结构矩阵就被采纳并用于更新全局信息素规则。

(4)

式中：ρ为信息素挥发系数；1-ρ为信息素残留因子，ρ⊂[0,1)； Δτij为本次路径Eij上的信息素增量，初始时刻Δτij(t)=0。

式(5)为本文中计算公式。

(5)

2) 启发式信息η。每增加一个新的局部结构(即有向边Eij)，用式(3)计算该结构对应的得分。蚂蚁状态转移规则：在搜索过程中，蚂蚁根据各条路径上的信息量及路径的起发信息来计算状态转移概率P。

(6)

式中：allowedk为蚂蚁k下一步允许选择的节点；α为信息启发式因子，表示轨迹的相对重要性；β为期望启发式因子，表示起发信息在蚂蚁选择路径中的受重视程度；ηij(t) 为启发函数；τij(t) 为信息素。

3) 网络生长规则：采用由上至下的网络增长模式，随机选择初始节点及后续生长节点。在选择后续节点生长位置时，通过局部打分函数判断该节点与已有结构各节点间的条件独立性，得到合理的生长结构，根据各结构得分确定概率，随机选择最终生长结构。MIT局部打分函数[4]如式(7)所示，用于判断Xj与Xi在Pa(Xi)情况下是否独立。

(7)

2.2S-ACOB的算法描述

1) 局部结构搜索程序。

步骤1。输入的剩余目标节点集合Va、已计算节点集合Vb。

步骤2。根据局部打分函数，判断Vb(j)是否适合作为Va(i)父节点，若计算结果大于零，则将Vb(j)加入到Va(i)的父节点集合Pa(Va(i))中。

步骤3。将Va(i)与其对应父节点以邻接矩阵表示，得到局部结构STU(i)。

步骤4。根据式(3)计算得到局部结构集合STU对应的得分集合g。

步骤5。输出结构集合STU与其对应得分集合g。

2) 蚁群主控程序。

步骤1。输入数据集D 、规定最大迭代次数Nmax、蚂蚁数目m。

步骤2。第N次迭代中，第i只蚂蚁在目标节点集合Vall中随机选择一个节点加入已计算节点集合Vb中，剩余目标节点集合为Va。

步骤3。通过结构搜索算法得到局部结构集合STU与其对应得分集合g。

步骤4。根据局部结构得分g与全局信息素Tau，确定状态转移概率PVa。

步骤5。通过轮盘赌方式选定对应的局部结构STU*。

步骤6。将其中新增节点V*加入Vb中，更新剩余目标节点Va，将新的局部结构STU*加入到表示整体结构的邻接矩阵CM中。

步骤7。重复步骤3～6，得到完整结构Ri，计算得分Gi，并记录。

步骤8。重复步骤2～7，记录在N次迭代中局部最优结构R*。

步骤9。更新全局信息素Tau。

步骤10。重复步骤2～9，得到全局最优结构Rbest。

3模型预测效果分析

3.1数据来源

研究数据主要来源于荷兰国家事件管理中心的拖车管理部门，还有部分来源于警察和路政部门。数据记录了荷兰第4大城市乌德勒支2005年5月～9月共1 853件事件数据，其中完备数据为1 016条，事件所包含的具体信息见表1。

表1　交通事件影响因素及变量取值

对数据进行统计分析发现，交通事件持续时间分布在[0,435] min内，分布范围较广，但76%的样本中事件持续时间集中在120 min以内。为了进行合理有效的预测，对持续时间在120 min内的事件以10 min为区间进行分类，之外的时间以20 min为区间进行分类。分类后的交通事件持续时间见图1。

图1　分类区间内交通事件发生次数Fig.1　Frequency chart of classified traffic incident duration

3.2网络结构

本文采用MIT评分函数对数据集进行贝叶斯网络结构学习。结合S-CAOB算法，借助Matlab平台进行程序编写与数据分析，完成贝叶斯网络模型搭建。利用蚁群算法经过反复迭代后得到最优网络结构，见图2，对应得分为10 922.54。基于评分搜索的方法，是针对数据集进行结构学习，图中的箭头并不表示因果联系，只能说明因素间相互影响。

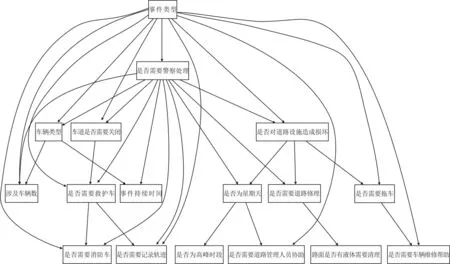
图2　全局贝叶斯网络图Fig.2　Global structure of Bayesian network

由图2可见，“事件类型”作为根节点影响着整个系统的复杂程度；“是否需要警察处理”直接或间接的影响的大部分节点，对于一些较为严重的事件，需要警察进行协调、处理，警察的参与会导致处理时间的延长。将与“事件持续时间(N4)”的无关的因素排除掉，得到结构见图3。

图3　局部贝叶斯网络图Fig.3　Partial structure of Bayesian network

“车辆类型(N2)”、“是否需要警察处理(N3)”直接影响着时间持续时间；“事件类型(N1)”作为影响“事件持续时间”父节点的因素间接影响着事件持续时间。其他因素可能对“事件持续时间”有着直接或间接的影响，但是在最优网络图上不够显著，因此为了便于直观分析予以排除。根据得到的网络结构，给出交通事件持续时间参数学习结果(P)，见表2。

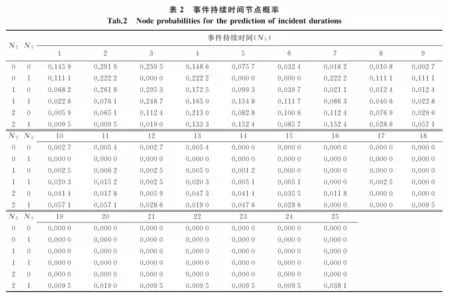
3.3概率预测

在交通事件响应过程中，已知部分或全部事件属性，可以推断交通事件持续时间的分布概率，同时结合样本数据，可评价贝叶斯网络的预测精度。由于节点属性较多，只给出部分属性下的概率预测图。

在不完全信息下，即能够观测1个或2个节点属性时，概率预测图见图4、图5。图3表明，在仅知道事件类型的情况下，不需要考虑其他因素，

即可对事件持续时间可能的分布概率进行快速的初步判断，并制定前期的应对方案，之后可再根据事件处理过程中不断反馈的其他信息进一步缩小持续时间的预测范围，或者调整可能持续时间的发生概率。

图4　事件类型为“抛锚”概率预测图Fig.4　Forecasting probability of "vehicle anchoring"

图5　事件类型为“抛锚”“不需要警察处理”概率预测图Fig.5　Forecasting probability of "vehicle anchoring""no police force"

在完全信息下，即能够观测全部节点属性时，预测概率与实际观测概率对比情况，如图6所示，预测后验概率仍然能够较好的描述实际观测概率。

图6　事件类型为“碰撞”“车辆类型小汽车”“不需要警察处理”概率预测图Fig.6　Forecasting probability of "crash""car" "no police force"

3.4研究对比

由于荷兰交通数据数据记录较为全面，很多学者采用不同的方法利用该数据进行研究。Wen等[11]构建了KNN模型，对于坠物、抛锚、事故三种事件类型的事件，预测误差小于15 min的比例分别为75.66%，67.25%，84.94%，但K值变化对预测精度影响较大，同时事件各属性的权重计算方法不合理，仅适用于二值变量。Wu等[12]构建了SVR模型，对于3种事件类型的预测误差小于15 min的比例分别为76.92%，68.82%，71.01%，但对于持续时间超过1 h的事件，抛锚和事故的预测误差小于15 min的比例分别只有33.33%和8.33%。说明SVR模型对于这类事件没有解释力。Ji等[13]构建贝叶斯决策树模型，3种事件类型的平均预测精度为73.57%，但决策树方法以节点间相互独立为前提条件，但实际情况下各种因素是相互影响的，故模型不能完全描述事件真实情况。

相比而言，贝叶斯网络模型能够直观的展现出变量之间的结构化关系，将事件属性对持续时间影响的内部机理揭示的更为透彻；能够准确的描述小概率事件，甚至通过参数学对部分未观测到的事件类型做出预测。本文构建的贝叶斯网络模型，总体预测精度达到87.82%。在数据完备情况下，需要描述的特征较多，模型预测精度相对较低为76.97%；在数据缺失的情况下，模型需要描述的特征较少，能够达到93.23%，认为模型能够描述现实情况。

图7　概率分布图Fig.7　Probability distributions

4结束语

笔者构建了以S-ACOB为核心的贝叶斯网络模型，并基于乌德勒支1 853条事件数据对该模型进行测试，筛选出“事件类型、车辆类型、是否需要警察处理”3项显著因素，对持续时间概率分布特征进行描述，模型平均预测精度达87.82%，证明该模型的可靠性及适用性，由此可见：

1) 贝叶斯网络在处理不完备数据集时的有效性，在减少观测样本的属性节点后，模型的预测精度没有受到影响，依然能够准确的描述持续时间分布特征。因此，本文所建模型能够通过较少的属性信息对事件进行快速反应，降低次生损失。

2) 贝叶斯网络基于实际观测数据进行分析，数据库越丰富，对持续时间概率分布的描述越准确。同时，对于现实情况下未观测到的交通事件，通过贝叶斯网络模型也能对其持续时间分布概率进行预测。

3) 通过S-ACOB算法搜索最优网络结构，其分布式并行计算大大提高了计算效率，证明了蚁群算法在解决贝叶斯网络最优结构搜索问题上是有效的。

4) 贝叶斯网络在描述总体分布时具有明显优势，而在预测总体分布下确定个体的延误时间将是本研究的发展方向。

参考文献

[1]GOLOB F T, RECKER W， LEONARD D J. An analysis of the severity and incident duration of truck-Involved freeway accidents [J]. Accident Analysis and Prevention, 1987, 19(4):375-395.

[2]SULLIVAN C E. New model for prediction incidents and incident delay [J]. Transportation Engineering, 1997, 123(4):267-275.

[3]OZBAY, KAAN, KACHROO P. Incident management in intelligent transportation systems [M]. Boston, MA: Artech House, 1999.

[4]CAMPOS de LUIS M. A scoring function for learning bayesian networks based on mutual information and conditional independence Tests [J]. Journal of Machine Learning Research, 2006(7):2149-2187.

[5]潘吉斯，吕 强，王红玲. 一种并行蚁群Bayesian网络学习的算法[J].小型微型计算机系统，2007:28(4)：651-655.

PAN Jisi, LYU Qiang, WANG Hongling. One kind of parallel algorithm of ant colony optimization to learn bayesian network[J]. Journal of Chinese Computer Systems, 2007:28(4)：651-655.(in Chinese)

[6]ZHONG Jijun, ZHANG Hongxun, HU Renbing, et al. A Bayesian network learning algorithm based on independence test and ant colony optimization[J]. Acta Automatica Sinica, 2009,35(3):281-288.

[7]DEMIROLUK S, OZBAY KAAN. Adaptive learning in bayesian networks for incident duration prediction [J]. Transportation Research Record: Journal of the Transportation Research Board, 2014, 2460:77-85.

[8]李大韦，程 琳. 交通事件持续时间预测贝叶斯网络方法研究[J]. 武汉理工大学学报:交通科学与工程版，2011，35(5)：884-887.

LI Dawei, CHENG Lin. Traffic incident duration prediction: A Bayesian network method [J].Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2011, 35(5):884-887. (in Chinese)

[9]张良力，祝 贺，马天宇.基于贝叶斯网络的机动车驾驶行为状态分析建模[J].交通信息与安全，2014，32(5)：77-82.

ZHANG Liangli, ZHU He, MA Tianyu. Model for vehicle drivers behavior analysis based on bayesian network [J]. Journal of Transpor Information and Safety, 2014, 32(5): 77-82 (in Chinese)

[10]杨 超，汪 超. 快速路交通事件持续时间预测模型[J].同济大学学报:自然科学版，2013，41(7):1015-1019.

YANG Chao, WANG Chao. Traffic incident duration forecast model of expressway [J]. Journal of Tongji University:Natural Science Edition, 2013, 41(7):1015-1019.(in Chinese)

[11]WEN Yuan, CHEN Shuyuan. Traffic incident duration prediction based on K-nearest neighbor[J]. Applied Mechanics and Materials Journal Impact Factor & Information, 2013(253/255):1675-1681.

[12]WU Weiwei, CHEN Shuyan. Traffic incident duration prediction based on support vector regression[J]. American Society of Civil Engineers, 2011,421:2412-2421.

[13]JI Yangbeibei, ZHANG Xiaoning, SUN Lijun. Traffic incident duration prediction based on the bayesian decision tree method[C]. 56thTransportation and Development Innovative Best Practices, New York, USA: TDIBP, 2008.

[14]郑长江，葛升阳，郑树康. 基于贝叶斯网络的交通事件持续时间预测[J]. 华东交通大学学报，2014，31(5):50-55.

ZHENG Changjiang, GE Shengyang, ZHENG Shukang. Traffic incident duration prediction based on bayesian network[J]. Journal of East China Jiaotong University, 2014, 31(5):50-55.(in Chinese)

[15]段海滨.蚁群算法原理及其应用[M]. 北京：科学出版社，2005.

DUAN Haibin. Ant colony algorithms: Theory and applications [M]. Beijing: Science Press, 2005 (in Chinese)

[16]高晓光，赵欢欢. 基于蚁群优化的贝叶斯网络学习[J]. 系统工程与电子技术， 2010，32(7)：1509-1512].

GAO Xiaoguang, ZHAO Huanhuan. Bayesian network learning on algorithm based on ant colony optimization [J]. Systems Engineering and Electronics, 2010, 32(7):1509-1512.(in Chinese)

Bayesian Network Model for the Prediction of

Traffic Incident Duration

MA Xuejing1SHAO Chunfu1▲QIAN Jianpei1WANG Tianyi2

(1.SchoolofTransportationComplexSystemsTheoryandTechnology,

BeijingJiaotongUniversity,Beijing100044,China;

2.NantongHenglongInformationEngineeringConsultants,Ltd.,Nantong22600,Jiangsu,China)

Abstract：Traffic incident is one of the main factors that lead to traffic congestions. Through controlling methods such as real-time traffic guidance, its impacts on traffic operation can be reduced. Accurately prediction of traffic congestion duration is a prerequisite for effective traffic control. Based on MIT scoring functions, an S-ACOB algorithm as the core of the Bayesian network model is developed. The networks are generated from top to bottom with an ant colony algorithm searching for the optimal network structure. To increase the robustness of the proposed Bayesian network, a random selection mechanism for the nodes and a partial probabilistic selection model for the local structure are introduced. Through an empirical study and comparative analyses, the average precision is up to 87.82%, which is superior to the alternatives reported in the previous research. regarding those nods with the complete and incomplete node properties, the accuracy of the network prediction model is up to 76.97% and 93.23%. The results show that this model can effectively predict the duration of traffic congestions.

Key words：traffic engineering; traffic incident; duration prediction; Bayesian network; structure learning; MIT algorithm; S-ACOB algorithm

通信作者：▲邵春福(1957-)，博士，教授. 研究方向：道路交通安全. E-mail：cfshao@bjtu.edu.cn

作者简介：第一马雪婧(1990-)，硕士研究生. 研究方向：交通安全. E-mail:13120880@bjtu.edu.cn

基金项目*国家自然科学(批准号：71210001)资助

收稿日期：2015-10-12修回日期：2015-11-19

中图分类号：U491.31

文献标志码：A

doi：10.3963/j.issn 1674-4861.2015.06.010