非均衡网络交通流动态演化规律研究*

柳　波　张　生

(1.江苏省城市规划设计研究院宿迁分院　江苏 宿迁 223800；

2.宿迁市城市规划设计研究院有限公司　 江苏 宿迁 223800；3.长沙理工大学交通运输工程学院　长沙 410004)



非均衡网络交通流动态演化规律研究*

柳波1,2▲张生3

(1.江苏省城市规划设计研究院宿迁分院江苏 宿迁 223800；

2.宿迁市城市规划设计研究院有限公司 江苏 宿迁 223800；3.长沙理工大学交通运输工程学院长沙 410004)

摘要为描述非均衡网络交通流实际成本-流量状态，考虑置存成本和路段行程时间，建立行程时间动态函数，将其引入用户均衡模型，构建基于出行总成本动态、路径流量动态、路段行程时间动态的交通流演化模型。利用简单网络，采用四阶龙格库塔方法对建立的模型进行数值模拟。动态模型弹性需求下，出行成本调整范围由大到小，趋于平衡值；路径流量迅速增加后，以较小调整范围，趋于平衡值；路段行程时间迅速增加后，逐步趋向于平衡值。固定需求下的出行成本、路径流量、路段行程时间均是反复调整多次后趋近于平衡值，调整范围缩小，次数增加。算例模拟结果表明，模型能够描述网络交通流从一种非均衡状态到另一种非均衡状态的动态调整过程。

关键词非均衡网络；交通流；动态演化；行程时间；四阶龙格库塔方法

*国家自然科学基金资助项目(批准号：51408058)、湖南省科技计划项目(批准号：2014GK3023)资助

0引言

服从 Wardrop 第一原理的网络交通流模式称为均衡网络流模式，否则称为非均衡网络流模式。研究者认为非均衡网络流模式是暂时的、不稳定的，均衡流才是稳定的，普遍存在于现实交通系统之中。因此，当这种均衡流模式遭到破坏后，出行者将根据掌握的交通信息，按照效用最大化原理调整自己的出行路线，一段时间以后又回到原来的网络均衡流模式，或者形成一个新的均衡网络流模式[1]。

国内外学者围绕网络交通流的这种非均衡特性展开了一系列的研究。国外学者Friesz[2-3]通过对逐日间网络交通流从一个均衡状态向另一个均衡状态的变化过程的研究，证明了交通流变化的动态非均衡性。Shah[4]提出了非均衡网络设计的思想。Iida[5]采研究出行者动态路径选择行为，表明网络交通流很难达到均衡状态。He[6]通过建立 “预测—修正”模型来描述中断后的交通网络逐渐发展为均衡的过程。国内学者连爱萍[7]针对均衡网络下交通流的变化进行分析。刘诗序等[8]揭示了均衡交通流平行解的唯一性。何胜学[9]提出了非稳定随机均衡分析的概念。李艳艳[10]从用户出行的角度对交通供求均衡与非均衡进行统一性描述，理论上证明交通供求的非均衡特性。黄中祥等[11]以最大化消费者剩余为目标，设计了动态非均衡网络模型。以往的研究并未构建处于非均衡网络状态下的交通流模型，无法反映交通流的动态变化规律，只能从侧面或反证交通流是处于非均衡网络下动态变化的。论文根据上述研究，以Samuelson[12]所提出的经济学均衡范例为基础，引入一个非均衡调整机制，构建非均衡网络交通流动态演化模型，从而达到描述网络交通流从一种非均衡状态到另一种非均衡的动态调整过程的目的。

1符号和假设

有关交通出行者和交通管理者的假设如下。

1) 出行者或管理者能够操纵任何路径上的出行成本和交通流量。

2) 当路网处于非均衡状态时，可通过成本、供需等相互影响，使交通出行系统围绕均衡状态波动。

3) 管理者可以依据交通需求预测自主选择道路资源供给。

4) 交通出行者和管理者掌握当前路网的完整信息，并利用每一个机会来分别提高他们的效用。

论文使用静态用户均衡模型中通勤者路径选择的标准符号，在其基础上进行扩展，以反映动态和非均衡问题。相关符号含义如下。

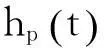
2非均衡网络交通流动态演化模型

Ganjalizadeh[13]提出如下用户均衡模型。

(1)

式中：α和β为过度函数的调制信号强度系数；κ和η控制对应于这些信号如何迅速进行调整。调制系数α和β决定相应过度函数值的调整灵敏度，参数κ和η表示相应调整过程的速度。

为了构建一个动态模型，使非均衡状态描述实际成本-流量状态，也就是可变现输出，本文对模型(1)进行改进。

首先，需要考虑非均衡的结果。一般一个时期内的过度供应会促进交通需求的增长，可能对出行成本产生影响[14]。因此，成本动态会被抑制或加强。另外，模型中需引入置存成本(由于道路供给资源不能及时投入使用或使用率较低造成管养成本等损失)，这些成本会影响供给和出行决策。

其次，将各路网节点之间的行程时间包括在内也是重要的[15]。第一，节点之间的行程时间必定影响交通流量，反过来交通流量的变化又会对行程时间产生影响；第二，行程时间对实际发生的出行数量具有很大影响。因为由于出行成本的制约，距离较近的节点，有利于管理者和出行者对非均衡交通状态做出迅速响应。

鉴于以上分析，将置存成本引入成本动态，同时重点考虑路段行程时间的影响，建立路段行程时间动态函数，加入模型(1)中，构建基于出行总成本动态、路径流量动态、路段行程时间动态的交通流演化模型。

首先将连接i∈NO,j∈ND的路径p∈Pij上的路段a∈Ap的过度交通流量表示为：

(2)

为了研究路段行程时间动态，进一步定义：

路径行程时间动态由(3)和(4)直接得到

(5)

(6)

将式(6)作为非均衡网络交通流演化动态模型(DM)。其中λ是过度函数的调制信号强度系数，决定相应过度函数值的调整灵敏度；γ控制对应于这些信号如何迅速进行调整，表示相应过程的调整速度。

3数值模拟

四阶龙格库塔方法是一种间接运用Taylor公式，得出较高阶数值公式的方法。该方法求解微分方程的精度较高。利用传统的 BPR函数(路段行程时间函数)形式和四阶龙格库塔方法进行数值模拟。对于包含弹性需求的例子，假设通勤者的总数固定，但是道路使用者的数量相对成本是灵敏的，因为他们可以选择一个使用方式。依照现有的传统，使用二元逻辑模型来描述方式选择。

为观察模型式(6)描述的调整过程，以图1表示的简单网络(5条路段和4个节点)为例，通过设定初始条件和调整参数，进行多组实验。

图 1　5条线路实验网络Fig.1　Five lines of experimental network

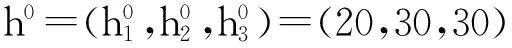
表1　路段成本函数的参数值

使用相同参数和初始条件，分别对弹性需求和固定需求下的DM进行数值实验。300时间单元弹性需求和固定需求的出行成本轨迹对比如图2，弹性需求和固定需求下路径流量轨迹对比见图3，弹性需求路段行程时间轨迹如图4，固定需求下路段行程时间轨迹如5。

图2　弹性需求与固定需求下DM的出行成本轨迹对比Fig.2　DM travel costs path contrast under elastic demand and fixed demand

图3　弹性需求与固定需求下DM的路径流量轨迹Fig.3　DM route flow path contrast under elastic demand and fixed demand

图4　弹性需求下DM的路段行程时间Fig.4　DM link travel time under elastic demand

图5　固定需求下DM的路段行程时间Fig.5　DM link travel time under the fixed demand

由动态模型在弹性需求和固定需求下的出行成本、路径流量、路段行程时间轨迹可知。

1) 弹性需求下DM出行成本第一个300时间单元内大部分时间在平衡值周围振荡，振荡幅度由高至低变化，最终趋向于平衡值，且平衡值与初始值近似相等；路径流量轨迹趋向于平衡值周围振荡，所有3条路径上的DM流量首先从初始值开始移动，它们以大约20个至30个时间单位上升至最高水平，之后又以大概20个时间单位下跌，振荡范围逐渐缩小；路段行程时间在第一个100时间单元内振幅较高，之后逐步降低，在第一个300时间单元范围内趋向于平衡值周围振荡，且平衡值高于初始值。

2) 固定需求下，出行成本、路径流量、路段行程时间均是反复调整多次后移动至接近的平衡值，与弹性需求下的对应动态变化趋势保持一致，不同之处在于轨迹振荡范围缩小，振荡次数增加。

4结束语

通过引入路段行程时间动态函数，笔者提出了基于出行总成本动态、路径流量动态、路段行程时间动态的非均衡网络交通流演化动态模型，描述了实际时变交通流和成本调整过程中的非均衡状态，以及由非均衡状态到均衡状态的调整过程。相比传统的均衡网络设计模型，考虑了由于网络路段(或节点)通行能力改变所引起的潜在的非均衡，可实现最优可行设计。而数值模拟实验验证了模型的有效性。但是由于数值模拟过程中仅使用了简单路网进行实验，对于多起点多终点复杂交通网络的适用性有待进一步验证。此外笔者所提出的模型仅对1 d内的交通流演化规律进行研究，对于结合当天和逐日间的动态演化模型，是后续研究重点之一。

参考文献

[1]黄中祥.对城市交通规划理论与方法的反思[J].长沙理工大学学报:自然科学版,2006,3(3):49-53.

HUANG Zhongxiang. The opinion on urban traffic planning theory and method l[J].Journal of Changsha University of Science and Technology:Natural Science Edition,2006,3(3):49-53.(in Chinese)

[2]FRIESZ T L, LUQUE J, TOBIN R L, et al. Dynamic network traffic assignment considered as a continuous time optimal control problem[J]. Operations Research, 1989, 37(6): 893-901.

[3]FRIESZ T L, BERNSTEIN D, MEHTA N J,et al. Day-to-day dynamic network disequilibria andidealized traveler information systems[J].Operations Research, 1994, 42(6): 1120-1136.

[4]SHAH S J. A dynamic disequilibrium network design model[D].Fairfax, Virginia:George Mason University,1999.

[5]LIDA Y, AKIYAMA T，UCHIDA T. Experimental analysis of dynamic route choice behavior[J]. Transportation Research Part B, 1992, 26(1): 17-32.

[6]HE X Z, LIU H X. Modeling the day-to day traffic evolution process after an unexpected network disruption[J].Transportation Research Part B,2012,46:50-71.

[7]连爱萍.城市动态网络交通流分配及相关问题的研究[D].北京:北京交通大学,2007.

LIAN Aiping. The research of urban dynamic network traffic flow distribution and related problems[D]. Beijing: Beijing Jiaotong University ,2007.(in Chinese)

[8]刘诗序,关宏志,严 海.网络交通流动态演化的混沌现象及其控制[J].物理学报,2012,61(9):1-10.

LIU Shixu, GUAN Hongzhi,YAN Hai. Chaotic behavior in the dynamical evolution of network traffic flow and its control[J].Acta Phys. Sin, 2012,61(9):1-10. (in Chinese)

[9]何胜学,范炳全.城市交通网络非稳定随机均衡分析[J].中国公路学报,2008,21(3)：101-105.

HE Shengxue, FAN Bingquan. Analysis of unsteady stochastic equilibrium on urban traffic network[J].China Journal of Highway and Transport,2008,21(3)：101-105. (in Chinese)

[10]李艳艳.城市交通供求非均衡特性研究[D].长春:吉林大学,2011.

LI Yanyan. Research on disequilibrium characteristic of urban traffic supply and demand[D].Changchun: Jilin University, 2011. (in Chinese)

[11]黄中祥,许泽昭.非均衡动态网络设计模型及求解[J].长沙理工大学学报:自然科学版,2015,12(1):18-22.

HUANG Zhongxiang, XU Zezhao. Design model and solving of non-equilibrium dynamic network[J].Journal of Changsha University of Science and Technology:Natural Science Edition,2015,12(1):18-22.(in Chinese)

[12]SAMUELSON P.A. Spatial price equilibrium and linear programming[J]. The American Economic Review, 1952,42(3): 283-303.

[13]GANJALIZADEH S. Dynamic adjustment processes in the study of traffic-network disequilibrium[D]. Fairfax, Virginia:George Mason University,1993.

[14]VARIAN H R. Microeconomic Analysis[M].New York:W W Norton,1984.

[15]FISHER F M. Disequilibrium foundations of equilibrium economics[D].Cambridge, UK,Cambridge University,1983.

A Study of the Evolution of Traffic Flow Dynamic

of a Disequilibrium Network

LIU Bo1,2▲ZHANG Sheng3

(1.SuqianBranchofJiangsuInstituteofUrbanPlanningandDesign，Suqian223800，Jiangsu，China;

2.SuqianInstituteofUrbanPlanningandDesignCompanyLimited，Suqian223800，Jiangsu，China;

3.SchoolofTraffic&TransportationEngineering，ChangshaUniversityofScience&Technology，

Changsha410004，China)

Abstract：To describe the cost-flow relationship of disequilibrium traffic flow, a function for modeling dynamic travel time is established considering the carrying cost and travel time. A flow model of dynamic traffic is developed based on total travel cost, path flow, link travel time and coupled with a user equilibrium model. A numerical simulation is carried out using a simple network and the fourth order Runge-Kutta method to test the created model. Under the elastic demand of dynamic model, travel cost ranges from large to small, then approaches to an equilibrium value. After a rapid increase of path flow, with a smaller adjusting range, it tends to approach to an equilibrium value. After a rapid increase in travel time, it gradually approaches to an equilibrium value. The travel cost of fixed demand, flow path and travel time approach to an equilibrium value after repeating adjustments several times with a small range. The simulation results show that the model can accurately describe the adjustment process of network traffic flow from one disequilibrium statue to another.

Key words：disequilibrium network； traffic flow；dynamic evolution；travel time；fourth order Runge-Kutta method

通信作者▲第一作者()简介：柳波(1987-)硕士，助理工程师.研究方向：交通运输规划与管理.E-mail：liubo0727@163.com

收稿日期：2015-03-09修回日期：2015-11-30

中图分类号：U491

文献标志码：A

doi：10.3963/j.issn 1674-4861.2015.06.009