秩距离广义BCH码的最小秩距离
2015-02-24潘桔
潘 桔
(沈阳大学 师范学院, 辽宁 沈阳 110044)
秩距离广义BCH码的最小秩距离
潘桔
(沈阳大学 师范学院, 辽宁 沈阳110044)
摘要:证明秩距离广义BCH码的最小秩距离与其校验矩阵的任一k阶子式构成的行列式的非零性有关,而与广义连续根集无关.
关键词:线性化多项式; 秩距离; 广义BCH码; 校验矩阵
秩距离码的概念和极大秩距离码的理论是1985年由俄国学者Gabidulin首先提出的,由于用秩距离码构造的各种密码体制和认证系统要比Hamming距离度量码的安全性更高,所以,近年来在通信与密码学的研究领域中受到广泛关注.2000年以来,我国学者杜伟章,王新梅等人以此理论为基础, 在文献[1-3]中给出了一些秩距离缩短码、秩距离码的构造方法,并且提出了一种新的码字----秩距离BCH码的概念,讨论了其最小秩距离的问题.他们指出秩距离BCH码的最小秩距离问题与其生成多项式的根集情况有关:当所给秩距离码的生成多项式具有广义连续根集时,它的最小秩距离问题是可以解决的; 而当其生成多项式根集为一般形式时,其最小秩距离及构造极大秩距离码却是悬而未决的问题.
1线性化多项式的概念和性质
线性化多项式的概念及其相关理论是研究秩距离码的重要工具,尤其是其根的存在性理论在求最小秩距离的研究中起着至关重要的作用.
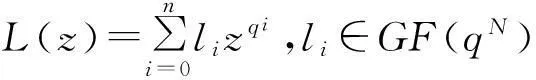

乘法运算为
定义2[5]6设L(x)和L1(x)是GF(qN)上的线性化多项式,如果存在GF(qN)上的线性化多项式L2(x)使得L(x)=L1(x)L2(x)成立,则称L1(x)能够符号整除L(x).
2秩距离的相关概念
定义3[5]7设GF(qN)中任一元素xi=ai1α1+ai2α2+…+aiNαN,i=1,2,…,n, 其中α1,α2,…,αN是GF(qN)在GF(q)上的一组基,则对x=(x1,x2,…,xn)T∈GF(qN)n有
称矩阵A(x)的秩为x在GF(q)上的秩,记为r(x;q);并将GF(qN)n中任意两个不同的元素x,y之间的秩距离定义为两者的差在GF(q)上的秩, 即
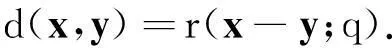
定义4[6]设矩阵H中的元素属于GF(qN),其在GF(q)上的极大线性无关列数称为该矩阵在GF(q)上的秩,记为r(H;q);在GF(qN)上的极大线性无关列数称为该矩阵在GF(qN)上的秩,记为r(H;qN),显然有r(H;q)≥r(H;qN).
定义5[7]设C为一个线性码,其秩距离定义为任意不同码字间距离的最小值, 即

对于码长为n,维数为k且秩距离为d的线性码称为秩距离(n,k,d)码.
定理1对于任意线性码C, 其秩距离是所有码字中秩最小的码字的秩, 即

证明由定义5及定义7知码C的秩距离表示为
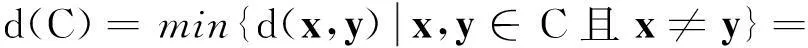

又因为C是一个线性码,所以有x-y=z∈C,那么码C的秩距离即为


引理1对于任意线性(n,k,d)码的秩距离d都有d≤n-k+1, 并且称能够达到这个最大值的码为极大秩距离码.
定理2设C是GF(qN)上的线性秩距离码, 其校验矩阵为
则码C的秩距离为d当且仅当校验矩阵H的任意d-1列向量在GF(q)上都线性无关, 其中d≥2.
证明(必要性)设线性码C的秩距离为d,假设校验矩阵H有d-1列向量在GF(q)上是线性相关的,则不妨设向量h1,h2,…,hd-1线性相关,根据线性相关性概念在GF(q)中可以找到不全为0的常数a1,a2,…,ad-1使a1h1+a2h2+…+ad-1hd-1=0成立,写成矩阵乘法形式则有
即c=(a1,a2,…,ad-1,0,…,0)是C的一个码字,且r(c;q)≤d-1,与码的秩距离为d矛盾.
(充分性)设校验矩阵H的任d-1列向量在GF(q)上都线性无关,要证码C的秩距离为d. 假设码C的秩距离为d-1, 则可设C中存在秩为d-1的码字c=(a1,a2,…,ad-1,0,…,0), 其中a1,a2,…,ad-1∈GF(q)且均不为零, 那么就有
即a1h1+a2h2+…+ad-1hd-1=0,这与H的任意d-1列向量在GF(q)上都是线性无关的是相矛盾的, 因此码C的秩距离为d.
3秩距离广义BCH码及其秩距离

例如,令G(z)=α5z[2]+α4z[1]+z为定义在GF(23)上的一个线性化多项式,其中α是GF(23)中的本原元素,且满足α3=α2+1.经过验证可得α[3]=1,(α2)[3]=1,即α和α2是GF(23)中的3级元素,且G(z)的根是α和α2在GF(2)上各种线性组合,那么由G(z)生成的线性码C就是广义BCH码.
定理3设G(z)是GF(qN)上的线性化多项式,若由G(z)可以生成一个秩距离广义BCH码C, 那么
(1) 码C的校验矩阵为
其中β1,β2,…,βk∈GF(q), 且G(z)的根是βi,i=1,2,…,k在GF(q)中的各种线性组合.
(2) 当校验矩阵H的任一k阶子式构成的行列式不为零时, 码C的最小秩距离为k+1,并且此时该码为极大秩距离码.
写成矩阵形式为
所以由G(z)生成的秩距离广义BCH码C的校验矩阵为

(2) 若校验矩阵H的任一k阶子式构成的行列式均不等于零,则有H中的任意k列向量在GF(q)上都是线性无关的,由定理3的内容可推知此码的最小秩距离为k+1.另一方面,设该码的维数为k′,则由线性码校验矩阵的定义可以得到n-k′=k,而它的最小秩距离为d=k+1=n-k′+1,即该码是极大秩距离码.
4结论
本文提出了秩距离广义BCH码的概念,讨论了其最小秩距离的问题,得到了秩距离广义BCH码的最小秩距离与其校验矩阵的任一k阶子式构成的行列式的非零性有关,而与广义连续根集无关,从而部分解决了杜伟章,王新梅等人提出的当其生成多项式的根集为一般情况时秩距离规律的问题.
参考文献:
[1] 杜伟章,王新梅. 关于秩距离BCH码的校验矩阵及其秩距离[J]. 通信学报, 2001,22(1):126-128.
(DUWZ,WANGXM.ParitycheckmatricesandrankdistanceofrankdistanceBCHcodes[J].JournalofChinaInstituteofCommunications, 2001,22(1):126-128.)
[2] 杜伟章,陈克非. 秩距离BCH码的进一步研究[J]. 通信学报, 2002,23(11):92-95.
(DUWZ,CHENKF.FurtherresearchonrankdistanceBCHcodes[J].JournalofChinaInstituteofCommunications, 2002,23(11):92-95.)
[3] 杜伟章,陈克非. 秩距离缩短码的构造[J]. 计算机学报, 2002,25(4):445-448.
(DUWZ,CHENKF.Theconstructionofrankdistanceabridgingcodes[J].ChineseJournalofComputers, 2002,25(4):445-448.)
[4] 冯克勤. 纠错码的代数理论[M]. 北京:清华大学出版社, 2010.
(FENGKQ.Thealgebraictheoryoferrorcorrectioncode[M].Beijing:TsinghuaUniversityPress, 2010.)
[5] 潘桔,关红钧. q-循环码的生成矩阵和校验矩阵[J]. 沈阳大学学报, 2008,20(4):6-8.
(PANJ,GUANHJ.Generatormatrixandcheckmatrixofq-cycliccodes[J].JournalofShenyangUniversity, 2008,20(4):6-8.)
[6] 陈博聪. 有限域上常循环码的研究[D]. 武汉:华中师范大学, 2013.
(CHENBC.Aresearchonconstacycliccodesoverfinitefields[D].Wuhan:CentralChinaNormalUniversity, 2013.)
[7] 钱建发,朱士信. 秩距离循环码的研究[J]. 计算机工程与应用, 2005,41(32):89-90.
【责任编辑: 胡天慧】
(QIANJF,ZHUSX.Thestudyofrankdistancecycliccodes[J].ComputerEngineeringandApplications, 2005,41(32):89-90.)
Minimum Rank Distance of Generalized Rank Distance BCH Code
PanJu
(Normal School, Shenyang University, Shenyang 110044, China)
Abstract:It proves that the minimum rank distance of a generalized rank distance BCH code is relative to any non zerok-th subdeterminant of its check matrix, and has nothing to do with the generalized continuous root set.
Key words:linearized polynomials; rank distance; generalized BCH codes; check matrix
中图分类号:TN 911
文献标志码:A
文章编号:2095-5456(2015)06-0512-03
作者简介:潘桔(1980-),女,辽宁营口人,沈阳大学讲师,博士研究生.
基金项目:辽宁省教育厅一般项目(L2015364).
收稿日期:2015-06-26
