高空风筝发电装置的预测控制

庄亚文，　袁德成，　魏志斌，　孙逸菲

(沈阳化工大学 信息工程学院, 沈阳 110142)



高空风筝发电装置的预测控制

庄亚文，袁德成，魏志斌，孙逸菲

(沈阳化工大学 信息工程学院, 沈阳 110142)

摘要：运用高空风筝发电装置的风力发电技术，建立了包括风筝局部位置和相对原点位置等的YOYO型风筝的动态模型。制定了风筝一个发电周期包括牵引、被动两个阶段的约束优化策略,应用非线性模型预测控制原理，解决了非线性实时优化的控制问题。仿真结果表明，非线性模型预测控制能显著改进其性能。

关键词：风筝发电; 预测控制; 非线性; 周期飞行

目前，世界上电能大约70%是利用化石能源(煤炭、石油、天然气)产生的[1]。由于化石能源是有限的，且污染环境；因此，人们开始探索新的清洁能源，对风能的关注也日益增加。预计2030年的能源成本，与煤炭、天然气等能源相比，高空风能成本是最低的[2]。

高空风筝发电是一种新型风力发电技术，通过控制风筝的双线，在气动升力的作用下而产生的电能。其原理是： 当风筝表面垂直于气流时，风筝的拉力最大，用风筝拖动地面上的卷扬机做功发电，动能转化为电能，即牵引阶段。当绳索用完风筝要返回时，风筝表面平行气流的拉力最小，卷扬机倒转拉回风筝，风筝耗电状态为被动阶段[3-4]。不断地进行两个阶段的循环，能量可以被得到。风筝的发电周期可分为牵引、被动2个阶段。在牵引阶段要求发电量最大，在被动阶段耗电量最小，故发电量明显高于耗电量[5]。

非线性模型预测控制是基于实时优化动态模型的反馈控制技术[6]。控制目标是使风筝按照周期轨道飞行并产生最大的电能。采用非线性模型预测控制原理设计YOYO结构风筝发电装置的控制器，可满足对风筝发电装置的需求。

1机理建模

风筝发电装置是由两条线控制其侧角，如图1所示。通过拉拽风筝的一条线来改变风筝的方向[7]。

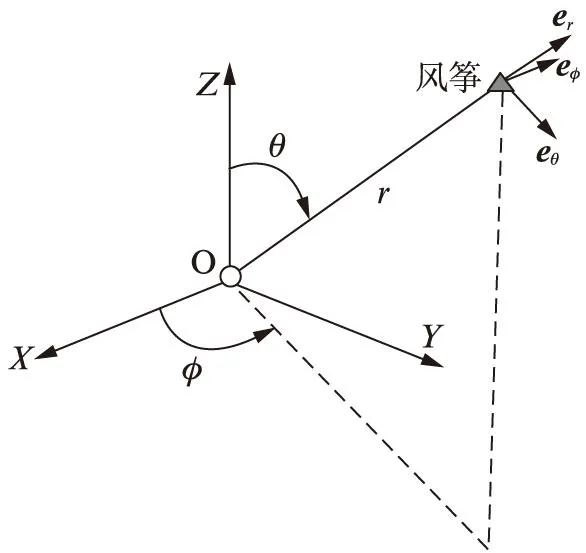
图1　风筝模型坐标系Fig.1　Coordinate system of the kite model

1.1　风筝动力学建模

空中风筝的运动模型可以用牛顿运动定律和空气动力学来表达[8]。应用极坐标θ、φ、r来表示相对于原点的风筝位置，即

p=(rsinθcosφ,rsinθsinφ,rcosθ)

其中，r为风筝到原点的距离；θ为风筝线与垂直方向的夹角；φ为风筝线投影到地面与X轴的夹角；rcosθ为风筝离地面高度[9]。

风筝移动坐标系统用单位向量eθ、eφ、er来表示，每1个单位向量是相对于极坐标θ、φ、r(见图1)。定义作用在风筝上的力为Fθ、Fφ、Fr，应用牛顿定律，风筝的力学表达式为

(1)

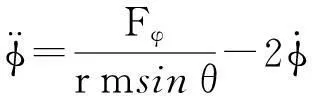
(2)

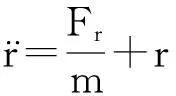
(3)

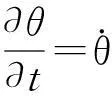
1.2　风筝气动升力和阻力

对模型的空气动力，首先要确定风筝的方向。假设风筝的尾部被拉到有效风的方向，在这种情况下，风筝的纵轴和有效风的向量方向是相同的[10]，即

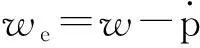
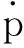
假设单位向量el是从风筝的前端指向后端，即

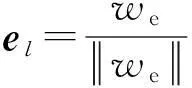
风筝横轴的单位向量et是从左翼的尖端到右翼的尖端，但是其必须正交于el。

et·el=0

(4)

单位向量et投影在单位向量er的坐标上可以确定两条线的长度差Δl，如图2所示。如果在风筝上两条线固定点的距离是d，从右到左固定点的向量为d·et。

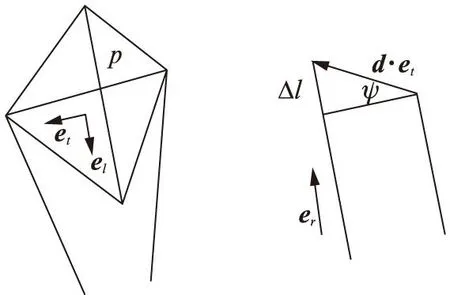
图2　风筝单位向量(左)和侧角(右)Fig.2　Unit vectors (L) and lateral angle (R)

控制量为风筝的侧角ψ，定义为

ψ=arcsin(Δl/d)

侧角决定了风筝的方向，即

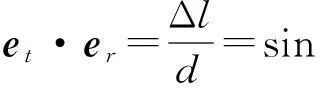
(5)

单位向量et须满足

(el×et)er>0

(6)

这确保了风筝和线总是相同方向的。对单位向量et满足式(3)~(5)。

et=e1(-cosψsinη)+e2(cosψcosη)+ersinψ

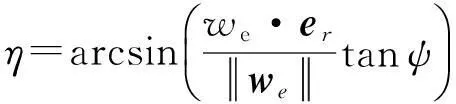
we是有效风向量到eθ、eφ的切平面上的投影，即we=we-er(er·we)。

定义正交单位向量

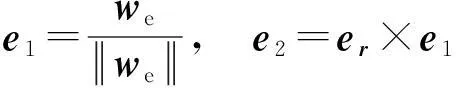
以便(e1,e2,er)满足正交右手坐标系定则。we在e2方向上没有分量，即

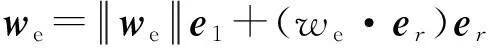
两个向量el×et、el分别是气动升力和阻力的方向。空气动力作用在风筝上的升力FL和阻力FD分别为

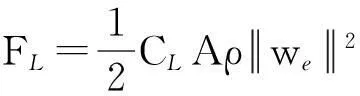
(7)

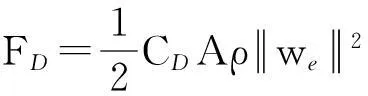
(8)

式中，A为风筝面积；ρ为空气密度；CL为升力系数；CD为阻力系数。

给定升力、阻力的大小和方向，能计算出空气动力

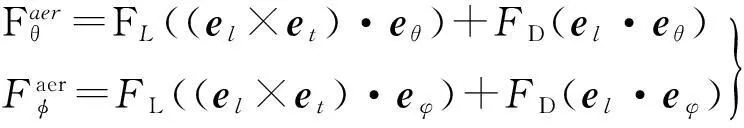
(9)

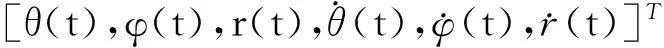
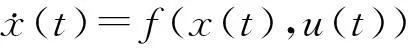
(10)

2模型预测控制

非线性模型预测控制是一种基于模型的优化控制算法，采用脉冲响应的非参数模型作为内部模型，根据对象的历史信息和未来输入，预测其未来控制输出[11]。

模型预测控制的具体优化过程： 在k时刻，根据状态变量计算出性能指标J的最优解，并且使用最优控制序列的第1个元素Δu(ki)作为输出；在k+1时刻，基于新的状态变量重新计算J的最优解，对原有的控制输出进行修正，再进行新的优化。因此，模型预测控制也被称为滚动控制[12]。

预测模型采用离散状态空间方程来表达。在预测模型的基础上，由系统控制量计算包括模型自由输出ym(k+i)和模型输出u(i)的模型预测输出：

yp(k+i)=ym(k+i)+u(i)

(11)

ym(k+i)=H(x(k))；i=1,2,…,i

(12)

式中，yp(k+i)为预测输出；x(k)为k时刻已知信息，包括过去时刻的控制量和输出量以及未来控制量的已知假设；H为对象预测模型的数学表达式。

自由输出是指k时刻的输出预测值是未考虑该时刻新加入的控制作用前作出的[13]。u(i)为在k时刻加入控制作用u(k+i)后新增加的模型输出。

经过误差补偿后的预测输出为

yp(k+i)=ym(k+i)+u(i)+e(k+i)

(13)

式中，e(k+i)为误差补偿。

参考轨迹通常选取

yr(k+i)=αiy(k)+(1-αi)c

(14)

i=1,2,…,i

式中，yr(k+i)为参考轨迹；y(k)为输出；c为设定值；αi=exp(-T/τ)，τ为参考估计时间常数；T为采样周期[14]。

优化的目标就是找到一组系数u(i)使整个优化时域尽可能接近参考轨迹。二次型性能指标为

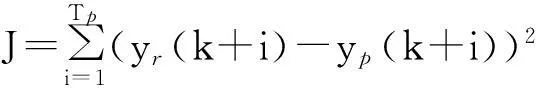
(15)

控制目标是通过合适的控制器作用在风筝上，使其按照周期轨道飞行并产生电能。非线性模型预测控制策略设计了风筝发电周期的2个阶段，根据各自的目标成本、状态约束、输入约束和终端条件。将系统离散化，选择一个适当的采样周期。每个采样时间tk，即性能指标

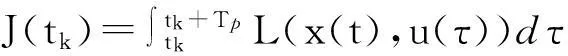
(16)

式中，Tp为预测时域；L(·)为基于各操作阶段的函数。

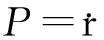
(1) 牵引阶段(发电)性能指标

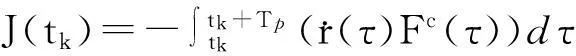
(17)

开始的状态条件为

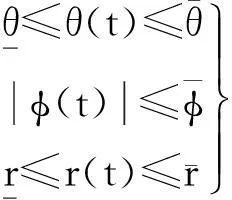
(18)

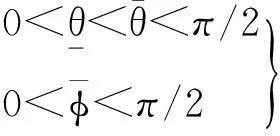
(19)

(2) 被动阶段(耗电)，该阶段分为3个子阶段，用最少的能量来回收风筝线，从而使总能量最大化。

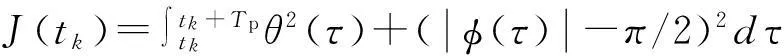
(20)

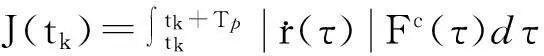
(21)

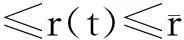
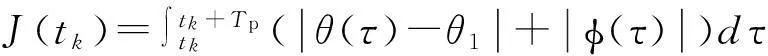
(22)

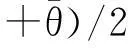
2个阶段均需要满足状态约束和控制量约束

(23)

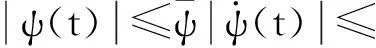
(24)

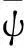
3仿真研究

根据建立的控制结构和模型预测控制器，对系统进行仿真研究。模型参数和各阶段约束条件见表1。

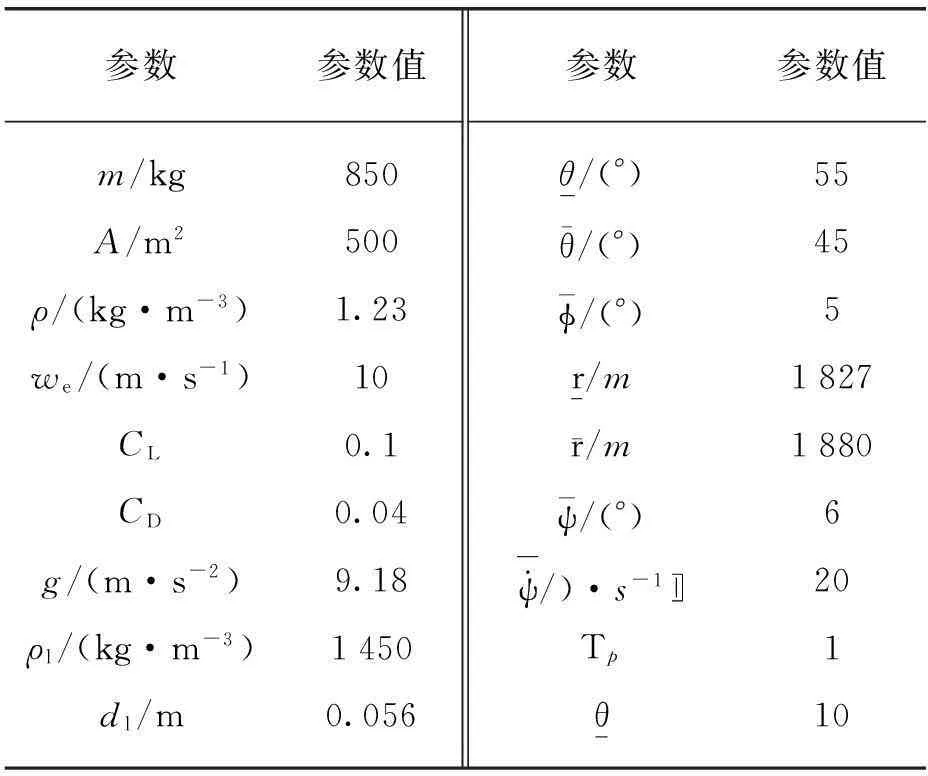
表1　模型参数和约束条件

仿真结果如图3~9所示。分别给出控制输入、风筝线长、风筝坐标系θ角和φ角、运行轨迹、输出电能的变化。

从图5可以看出，在仿真过程中，从发电阶段到电动阶段，每个周期线长的变化相对稳定。从图6和图7可见，风筝φ和θ角周期变化也相对稳定。图7风筝的运行轨迹满足周期轨迹“8”的要求。图9风筝产生的电能总体成线性增加。非线性模型预测控制能显著改进风筝发电装置的性能。

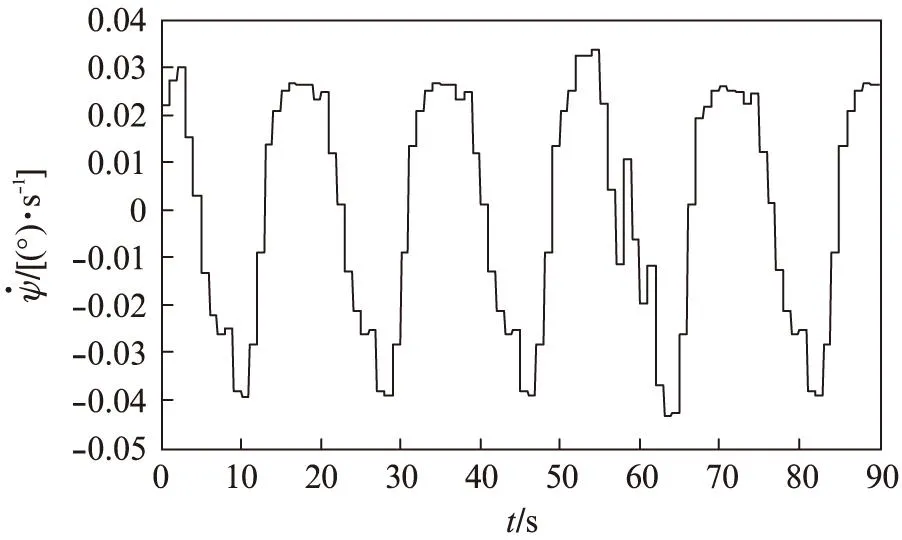
图3　控制量Fig.3　Control parameter

图4　控制量Fig.4　Control parameter　0

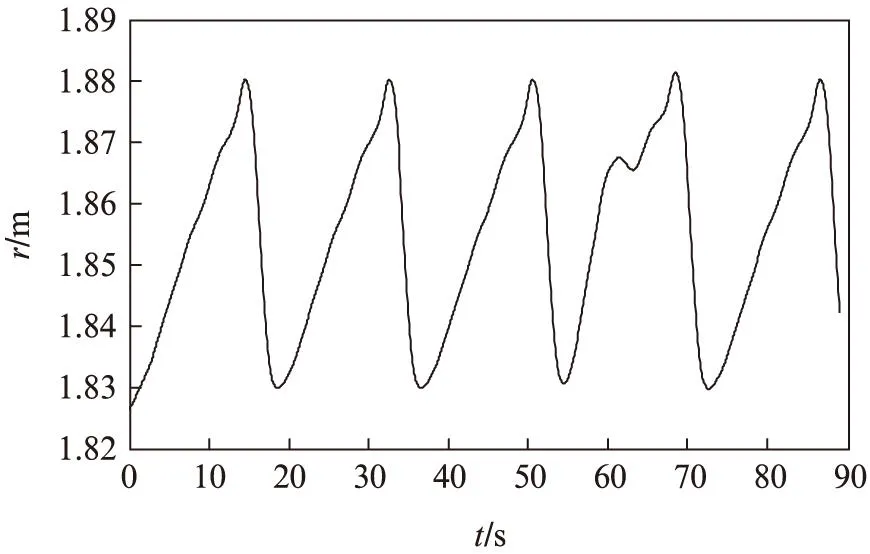
图5　风筝线长的变化Fig.5　Variance of line length

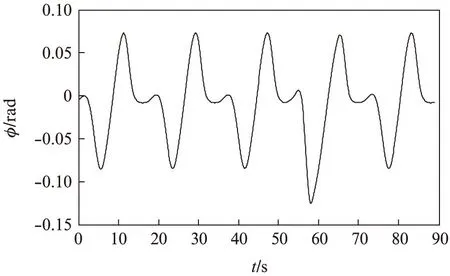
图6　风筝φ角的变化Fig.6　Variance of angle φ

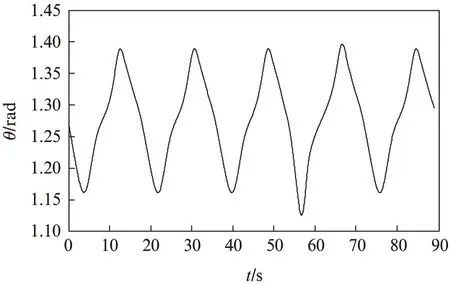
图7　风筝θ角的变化Fig.7　Variance of theta angle θ

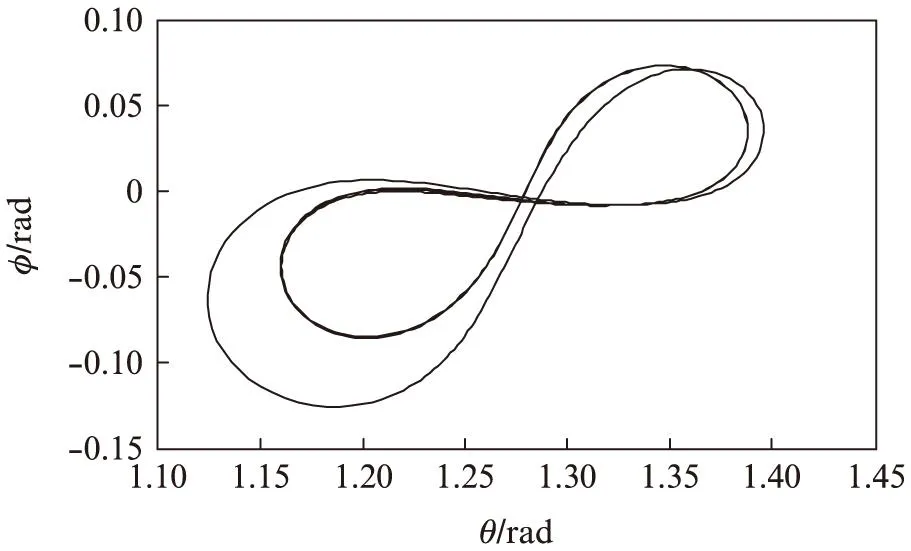
图8　风筝位置轨迹Fig.8　Orbit of kite

图9　风筝产生电量Fig.9　Energy generated by kite

4结语

模型预测控制能够处理风筝发电中存在的非线性、扰动以及约束条件等问题。为解决非线性实时优化的问题，本文采用模型预测控制设计非线性周期不稳定风筝系统，具体分析了YOYO结构风筝装置的发电周期各阶段的控制目标、约束条件。仿真结果验证了非线性模型预测控制对风筝模型的有效性。

参考文献：

[1]Fgiano L,Milanese M,Piga D.High altitude wind power generation[J].IEEE Transactions on Energy Conversion,2010,25(1)： 168-180.

[2]Canale M,Fgiano L,Milanese M.High altitude wind energy generation using controlled power kites[J].IEEE Transactions on control Systems Technology,2010,18(2)： 279-293.

[3]Ilzhöfer A, Houska B,Diehl M.Nonlinear MPC of kites under varying wind conditions for a new class of large-scale wind power generators[J].International Journal of Robust and Nonlinear Control,2007,17： 1590-1599.

[4]Williams P,Lansdorp B,Ockels W.Optimal cross-wind towing and power generation with tethered kites[J].Journal of guidance,control and dynamics,2007,31(1)： 81-93.

[5]Diehl M,Magni L,Nicolao G D.Efficient NMPC of unstable periodic systems approximate infinite horizon closed loop costing[J].Annual Review in Control,2004，28(1)： 37-45.

[6]Utgikar V P,Scott J P.Energy forecasting： Predictions,reality and analysis of causes of error[J].Energy Policy,2006,34(17)： 3087-3092.

[7]Houska B, Diehl M.Optimal control for power generating kites[C]∥European Control Conference(ECC).[S.L.]： IEEE,2007： 3560-3566.

[8]Thresher R,Robinson M,Veers P.To capture the wind[J].IEEE Power & Energy Magazine,2007,5(6)： 34-46.

[9]Mayne D Q,Rawlings J B.Model predictive control： theory and design[J].Process Automation Handbook,2012,130： 3430-3433.

[10]Canale M,Fagiano L,Milanese M.Power kites for wind energygeneration-fast predic-tive control of tethered airfoils.[J].IEEE Control Systems Magazine,2007,27(6)： 25-38.

[12]Diehl M,Bock H G,Schlöder J P,et al.Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations[J].J Process Control,2002,12(1)： 577-585.

[13]Diehl M,Findeisen R,Bock H G,et al.An efficient algorithm for nonlinear model predictive control of large-scale systems[J].At-Automatisierungstechnik,2003,51： 22-29.

[14]Roberts B W,Shepard D H,Caldeira K,et al.Harnessing high-altitud e wind power[J].IEEE Transactions on Energy Conversion,Special Issue on Wind Power 2007,22(1)： 136-144.

[15]孙衢,孙煜.高空风力发电机组预测函数控制研究[J].中国科学技术大学学报，2012,42(5)： 372-377.

指导教师: 袁德成(1960 -)，男，教授，博导，主要研究方向为混杂控制系统理论及应用，E-mail: yuandecheng@163.com

Predictive Control for High-Altitude Kite Generators

ZHUANGYawen,YUANDecheng,WEIZhibin,SUNYifei

(College of Information Engineering, Shenyang University of Chemical Technology,

Shenyang 110142, China)

Abstract：High-altitudekite generator is a new kind of wind power generation device. A dynamic model ofthe YOYO configuration kite is derived, including the local position and the positionrelative to the kite pilot. Energy is obtained by performing a two-phase cycle:traction phase and passive phase. An optimization problem of the two stages is formulated,and the generation controller is designed using a nonlinear model and the predictivecontrol principle to solve the optimal control problem of nonlinearity and real-timeproperty. Simulation results show that the predictive control with a nonlinear modelcan significantly improve performance of the kite generator.

Key words：kite generator;predictive control; nonlinear; periodic orbit

文献标志码：A

中图分类号：TM 315

文章编号2095 - 0020(2015)06 -0345 - 06

作者简介:庄亚文(1990 -)，男，硕士生，主要研究方向为复杂工业过程建模与控制，E-mail: 532186017@qq.com

收稿日期:2015 - 09 - 28