信息不对称条件下拆迁纠纷动态议价模型的构建与分析

秦中伏，张明涛

（浙江大学 建筑工程学院，杭州310058）

一 引言

近年来，由城市房屋拆迁引发的利益冲突、矛盾激化，乃至恶性事件屡见不鲜，被国内媒体称为“史上最牛钉子户”的重庆杨家坪拆迁案、被称为“最贵钉子户”的深圳蔡珠祥案等，都说明了房屋拆迁纠纷的妥善调解是保障并推动拆迁工作的重要内容。

在这样的背景下，对拆迁纠纷的研究已经成为近些年的热点之一，研究的切入点也各有不同，其中以博弈分析为主要手段的研究较为广泛。运用博弈论思想对拆迁纠纷进行定性分析方面，户邑等从纠纷参与人的角度出发，以拆迁管理为切入点，分析了政府部门与拆迁人之间的博弈行为，指出政府既是拆迁的管理者、协调者，也是纠纷中有关争议的仲裁者，并强调了政府在拆迁纠纷中角色的多重性［1］；Matthew S．Erie针对我国房屋拆迁纠纷中的“钉子户”现象，分析了媒体的介入对拆迁问题的解决产生的影响［2］；彭小兵、李钟书等借助博弈的基本思想，从纠纷当事人的角色定位、策略制定与调整、利益相互影响等方面提出了建议［3］［4］。在博弈论的分析方法的运用方面，钟蔚借助囚徒困境模型，对拆迁中强征、抗征、行贿、上访等行为对纠纷当事人的利益影响进行分析，从而为解决征地冲突提出了合理化建议［5］；朱念劬利用博弈矩阵和效用函数，对不同局势下拆迁纠纷当事人的收益进行了比较，并基于多阶段博弈模型提高了其研究成果与现实案例的吻合度，为当事人如何制定报价提供了指导［6］。从上述研究可知，利用博弈论基本思想对拆迁纠纷问题的研究需要建立符合现实状况的博弈模型。

在拆迁纠纷中，当事人在拆迁补偿额度上的争夺往往成为纠纷的焦点，这一补偿额度的争议过程可被视作讨价还价的过程。在这个过程中，当事者的还价受其保留价、时间压力、对手类型、对手让步模式与让步多少、预期的对手将来的出价等诸多因素影响，同时，还会受局中人可能产生的互惠心理、公平心理、自我满足感等主观情绪的影响［7］。为此，一些学者运用讨价还价理论探讨拆迁纠纷产生的原因、影响要素以及解决方法。讨价还价博弈的概念最早由纳什（John Nash）提出，通过分析效用测度的无关性、帕累托有效、无关选择的独立性和对称性，进而推导出纳什讨价还价解［8］。随后，马克·鲁宾斯坦（Mar k Rubinstein）建立了完全信息轮流出价条件下的鲁宾斯坦讨价还价模型［9］。结合工程建设纠纷的特点，Toshihiko Omoto等利用讨价还价模型对当事人如何在达成协议和申请仲裁之间做出选择给出了建议［10］。考虑到当事人的议价能力对议价结果也会产生的重要影响，郑鸿运用讨价还价模型和纠纷当事人的收益比较，阐述了议价能力对讨价还价的影响［11］46－50。考虑到拆迁纠纷问题中当事者之间往往是信息不对称性的，向钢华等对不完全信息相互威慑的讨价还价模型进行了设计和研究，分析了不完全信息条件下相互威慑讨价还价中的威慑可信性或冲突可能性［12］。从上述研究可以看出，基于议价过程的分析往往受到诸多主观因素影响，与此同时，传统分析的方式往往忽略了现实纠纷问题的主要特点，即信息的动态性和不对称性，所以需要构建更加符合现实要求的议价分析模型。

本研究旨在基于拆迁纠纷问题复杂多变的实际特征，在鲁宾斯坦讨价还价模型中将信息不对称性与动态性纳入分析中来，通过构建信息不对称条件下拆迁纠纷动态议价模型，对拆迁纠纷当事人给出补偿议价的过程做出解释，并对未来拆迁工作中拆迁补偿的合理制定以及对有可能发生的议价纠纷进行预测，这对实现拆迁工作中纠纷的规避和将纠纷造成的损失最小化具有现实意义。

二 鲁宾斯坦讨价还价模型在拆迁纠纷问题中应用的局限性

在拆迁纠纷案例中较为常见的是纠纷当事人（一般为被拆迁方）对拆迁补偿不能接受，并通过讨价还价行为使双方达成一个新的并被双方共同接受的补偿值。拆迁纠纷中的议价行为也属于讨价还价行为的一种。讨价还价的概念最早由John Nash于1950年提出。随着研究的不断深入，直至1982年，美国学者鲁宾斯坦（Ariel Rubinstein）建立了完全信息条件下轮流出价的讨价还价模型。这一模型在经济学界得到了广泛认可，同时也为本研究提供了分析思路，但这一模型在拆迁纠纷问题中的应用仍有一定局限性。

（一）鲁宾斯坦讨价还价模型简介

鲁宾斯坦基于“分蛋糕”问题对基本的、无限期的完全信息讨价还价过程进行了模拟，给出了完全信息条件下的轮流出价讨价还价模型，即鲁宾斯坦讨价还价模型。

在该模型中，参与人1与参与人2分割大小为π（π＞0）的蛋糕，由参与人1首先提出分配方案，在轮流出价的过程中，若参与人一方接受对方分配方案，则双方达成协议。鲁宾斯坦的分析思路是根据最后被接受的报价提出者的不同，为该参与人提出最“合理”的报价值，这一报价是根据两人议价能力（即贴现因子δ）而得出的一次性最优报价值。

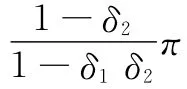
（二）鲁宾斯坦讨价还价模型在拆迁纠纷问题中应用的局限性

首先，在拆迁纠纷中的信息不是完全被局中人已知的。信息不对称现象对现实问题的影响已经在市场投资［13］与交易纠纷［14］等众多领域得到体现。而在拆迁纠纷问题中，信息不对称性主要表现在两个方面：一是局中人无法确定对方接受阈值是多少，所以“蛋糕”的大小理论上应该是未知的；二是局中人不能确定对方局中人的议价能力，任一局中人的真实议价能力都可能被故意掩饰［15］。

其次，拆迁纠纷议价过程中局中人的相关信息是动态变化的。从上述不同情况下的最优报价可知，当贴现因子与“蛋糕”大小已知的前提下，该最优报价是固定不变的，但是在现实的拆迁纠纷案例中，讨价还价是一个反复进行的过程，局中人在每一轮讨价还价过程中，自己的接受阈值和自信程度都可能发生改变，同时，局中人还会随着议价的进程不断更新对对方局中人相关信息的判断。

因此，需要在借鉴既往研究成果的基础上结合拆迁纠纷问题信息不对称性和动态性的实际特点，对议价过程的要素进行重新设定，并构建出符合现实特征的议价模型。

三 信息不对称条件下拆迁纠纷动态议价模型的构建

博弈论又称对策论，其理论早于1944年便已提出，而对其研究也不断深入，其中尤以美国数学家John Nash在20世纪50年代提出著名的“Nash均衡”这一概念为代表，不仅证明了非合作博弈及均衡解，也证明了均衡解的存在性。根据研究切入点的不同，逐渐有亚对策、软对策、误对策等理论的建立，而博弈类型也逐渐丰富，有合作博弈和非合作博弈、静态博弈与动态博弈、完全信息博弈与不完全信息博弈等不同分类。讨价还价行为属于博弈的一种，但由前文可知鲁宾斯坦讨价还价模型仅适用于无限期的完全信息讨价还价过程，所以需根据博弈分析的基本思想对上述模型进行完善。

（一）拆迁纠纷博弈的基本要素设定

从局中人的角度来看，虽然在现实的拆迁纠纷案例中常有政府、开发商、拆迁实施者和拆迁户等多个主体共同参与，但是由于本研究重点关注的是拆迁纠纷中当事者之间的议价过程，所以本研究将拆迁纠纷博弈中的局中人分为拆迁方和被拆迁方。

从局中人策略的角度来看，在现实的拆迁纠纷案例中，虽然局中人常见的行为一般有议价（即讨价还价，这其实是一个妥协或让步的行为）、劝说、威胁（或恐吓）、奖励（或许诺）等，但是由于本研究的侧重点在于拆迁纠纷中的议价过程。从拆迁纠纷的议价进程的角度来看，局中人的策略则可分为接受议价和不接受议价两类。如果局中人的任何一方接受当前对方提出的议价，则议价终止，拆迁得以实现。如果局中人的任何一方不接受当前对方提出的议价，则要么提出新的议价，议价过程继续进行，要么不再提出新的议价，等待对方接受自己的最后还价，如果对方接受自己的最后还价，则议价终止，拆迁得以实现，如果对方不接受自己的最后还价，则谈判破裂，议价终止。

（二）信息不对称条件下拆迁纠纷动态议价模型的要素设定

本研究对拆迁纠纷的议价环节做如下假定：局中人i（拆迁方）率先出价，此后双方在信息不对称条件下轮流出价，直到一方接受对方提议，或者谈判最终破裂，议价过程结束。在议价开始时以及议价过程中，双方都对自己的接受阈值（Plim）有所设定，且对对方的接受阈值有所预测；在议价过程中，双方根据自己在当前情况下通过议价行为夺得利益的能力（自信度δ）和对对方的自信度的评判，交替报出在当前情况下对自己最为有利的议价（P）。综上所述，可将信息不对称条件下拆迁纠纷议价模型记述为：G＝｛N，Plim，δ，P｝。其中，N ＝｛i，j｝，Plim＝ ｛Pmaxii，Pminjj，Pmaxij，Pminji｝，δ＝ ｛δii，δjj，δij，δji｝，P ＝｛Pi，Pj｝。各要素的定义如下：

N＝｛i，j｝表示拆迁纠纷中的局中人，其中i表示拆迁方，j表示被拆迁方；

Plim表示局中人的接受阈值，其中Piimax和Pimjax分别表示i（拆迁方）可以给出的拆迁补偿的最高价以及j（被拆迁方）对这一最高补偿价的估计，Pjmjin和Pjmiin分别表示j（被拆迁方）所能接受的拆迁补偿的最低价以及i（拆迁方）对这一最低补偿价的估计；

δ表示局中人的自信度，其中δii和δij分别表示i（拆迁方）自己的自信度的大小以及j（被拆迁方）对i的自信度的估计，δjj和δji分别表示j（被拆迁方）自己的自信度的大小以及i（拆迁方）对j的自信度的估计；

P＝｛Pi，Pj｝表示拆迁纠纷中的局中人所给出的各自的议价值。

而在不同的议价阶段（t），各方的接受阈值（包括对对方接受阈值的预测值）、各方自信度（包括对对方自信度的评判）以及在议价过程中的实际报价都会有所不同。因此，该模型还可以记述为：G（t）＝｛N，Plim（t），δ（t），P（t）｝，模型中各要素的具体形式与含义与上述表达类似。

（三）信息不对称条件下拆迁纠纷动态议价模型的构建

根据鲁宾斯坦讨价还价模型在拆迁纠纷中的适用性分析可知，在推导拆迁纠纷议价值P（t）的过程中必须要考虑信息不对称性和动态性。

首先要确定“蛋糕”的大小。在任何一轮议价时，局中人议价的起点都是自己上次的报价，而对于局中人来说能得到最多的利益就是对方局中人的接受阈值，但受信息不对称性的影响，这一接受阈值的大小仅能靠局中人估测。因此，在第t次议价时，对i（拆迁方）而言，其上一次报价值是Pi（t－1），此时i根据j已经给出的Pj（t－1）推测出其新的接受阈值为Pjmiin（t－1），所以，对于i来说，“蛋糕”大小为Pjmiin（t－1）－Pi（t－1）。同理，对j（被拆迁方）而言，其上一次报价值是Pj（t－1），j根据i已经给出的Pi（t）推测出其新的接受阈值为（t），所以对于j来说，“蛋糕”大小为Pj（t－1）－Pimjax（t）。

其次，自信度δ是影响局中人议价报价的重要因素之一，引入自信度的概念用以表示纠纷当事人通过议价行为赢得目标报价的信心与能力，自信度随时受到双方议价情况的影响，也进一步影响双方进一步议价值的确定。己方自信度越高，越不容易对“蛋糕”做出让步；与此同时，对方自信度越高，越容易从己方争得更多的“蛋糕”。与鲁宾斯坦讨价还价模型中贴现因子类似，自信度δ∈［0，1］，当δ＝0时，表示局中人完全失去了议价的能力，协议的最终报价将由对方主导；当δ＝1时，表示局中人有足够的能力主导协议的议价值的最终确定。在信息不对称条件下，影响局中人做出报价的是己方自信度和对对方局中人自信度的估计值。

综上所述，可将信息不对称条件下拆迁纠纷动态议价模型表达如下：

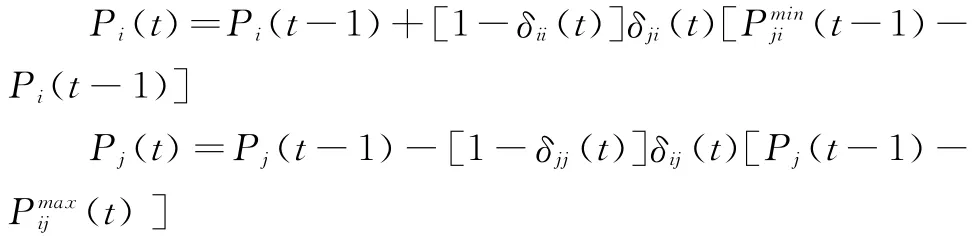
其中t≥1。

（四）自信度的影响因素与计算方法

在拆迁纠纷议价过程中，对对方当事人自信度的判断，主要受到对方当事人报价、对对方当事人接受阈值的预测值的影响，同时也与对对方信息表述的真实性判断有关。

首先，对方连续报价的变化幅度可以体现对方自信度的高低，两次报价变化幅度越小说明其自信度越高，反之亦反。以拆迁方预测被拆迁房自信度为例，可表示如下式：

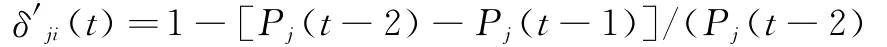
式中t≥2

其次，对方报价与对对方当事人接受阈值的预测值的差距也是己方当事人判断对方自信度的主要依据，两者差距越小，说明对方自信度较高，反之亦反，可表示如下式：

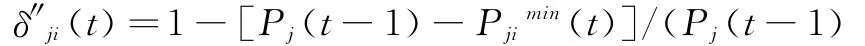
式中t≥1

上述两式，前者是仅依据对方提供的信息进行判断，后者则是己方当事人根据自己的预测进行判断，定义真实性判断系数τ（t），令0≤τ（t）≤1，其中τ（t）越趋近1，表示越相信，反之则表述不相信，则基于上述两式可以得出对对方当事人的自信度预测值表达式如下：

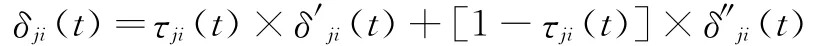
式中t≥2，而当t＝1时，被拆迁方还没有连续报价，所以只能通过δ″ji（1）进行评价。

同理，被拆迁方对拆迁方的自信度预测的公式可以用如下公式表示：

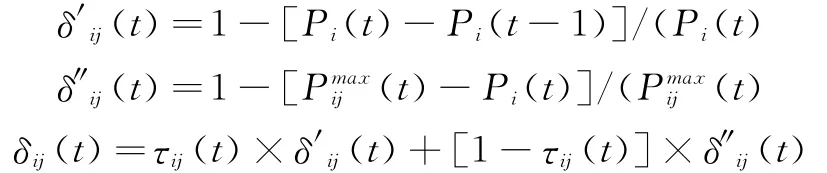
上式中均有t≥1，当己方当事人对对方当事人自信度有了预测之后，则自身自信度会受到影响、发生变化。基于当事人的非理性特征，当双方当事人自信度出现差异时，当事人会出现非理性情绪，如嫉妒、愤怒、攻击等对抗情绪，或者如同情、谦让、互利等合作情绪。分别用α和β表示当事人的对抗情绪敏感系数和合作情绪敏感系数，令α∈［0，1］且β∈［0，1］，当α（或β）越大，说明当事人容易被对方当事人的自信度所影响，相反地，当α（或β）越小，说明当事人越坚持自己的自信、不受对方影响。根据前文的分析，可将己方当事人自信度表达式表示如下：

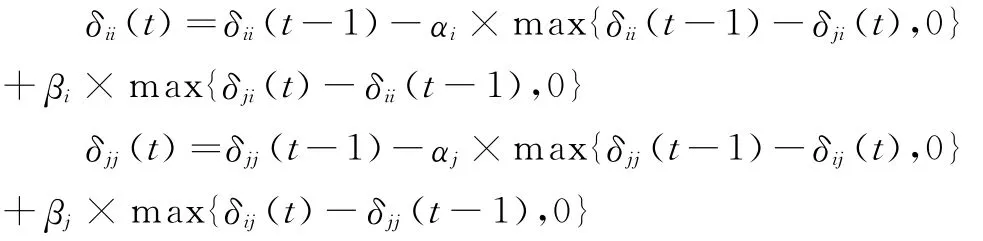
此处有t≥1。

四 基于信息不对称条件下拆迁纠纷动态议价模型的案例分析

基于信息不对称条件下拆迁纠纷动态议价模型，我们以被称为“温岭最牛钉子户”的罗保根拆迁案为例，通过模型构建与不同条件下的议价演算验证该模型的适用性，并为如何在现实拆迁纠纷中规避、化解议价纠纷提供解释。

（一）案例简介与模型构建

温岭市火车站建设过程中，被征地农户罗保根一家因不能接受拆迁补偿方案而拒绝搬迁，其5层楼房屹立在新修建的马路中间，经过该路段的车辆行人都得绕行而过，后经媒体报道后，被网民称为“最牛钉子户”。2008年，初次测量评估时，罗保根了解到自家粗略的评估价在28万元左右，罗觉得“再商量下应该可以更高些，加个一两万总还是可以的，那就还可以接受”，但按照相关规定给出的最高补偿额仅为26万元，罗表示不能接受并拒绝该补偿协议。2009年，温岭站落成，站前大道的建设于2011年春天动工，2012年夏季拆迁作业开始实施，由于罗家房屋在邻居拆迁中受损，家中矮房也在家中无人时被拆迁方私自拆除，双方关系日渐紧张。事件经报道后，政府相关部门开始介入，而此时罗家提出至少80万拆迁补偿才能同意拆迁，双方僵持不下后，各级政府部门加强了与罗家的沟通协商，11月30日罗保根接受原补偿标准，12月1日罗家原有住宅完成拆迁。

在此案例中，仅仅8天之内，罗保根一家的态度就从之前的“坚决不能接受”变成了“接受原拆迁补偿方案”。针对该过程的猜想与分析，也成为了该事件结束后的话题热点。为了更好地验证该模型对拆迁纠纷议价的解释作用，可根据已知信息将基于本案例的信息不对称条件下拆迁纠纷动态议价模型构建如下：

局中人，即拆迁纠纷当事人N＝｛i，j│其中i为政府，j为被拆迁方罗保根｝；

策略，双方策略均设定为接受协议并拆迁、不接受协议并继续谈判；

纠纷起点，即t＝0，设定为罗保根要求80万元补偿；

当任何一方的报价都超出了对方的接受阈值时，议价继续进行，当有一方的报价被对方接受，则议价终止。

（二）基于不同条件设定下的演算分析与解释

在上述案例的询价阶段中，t＝0，政府给出其在相关政策规定下所能给出的最高补偿26万元，而罗保根提出要求补偿80万元方可接受拆迁，但是其接受阈值是在28万元的基础上再多补一两万，设其为30万元，故有如下表达：（单位：万元）

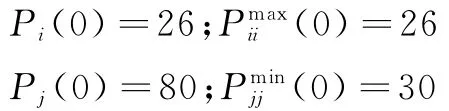
此时由于有 Pi（0）＜ Pminjj（0），且 有 Pj（0）＞Pminii（0），所以双方都不会接受对方报价，并进入议价阶段。

为了验证在不同自信度水平下双方在议价过程中将给出不同程度的议价变化幅度，可对纠纷当事人双方的自信度水平做（强，强）、（强，弱）、（弱，强）、（弱，弱）四种假设，根据议价模型公式可得出如下运算结果：

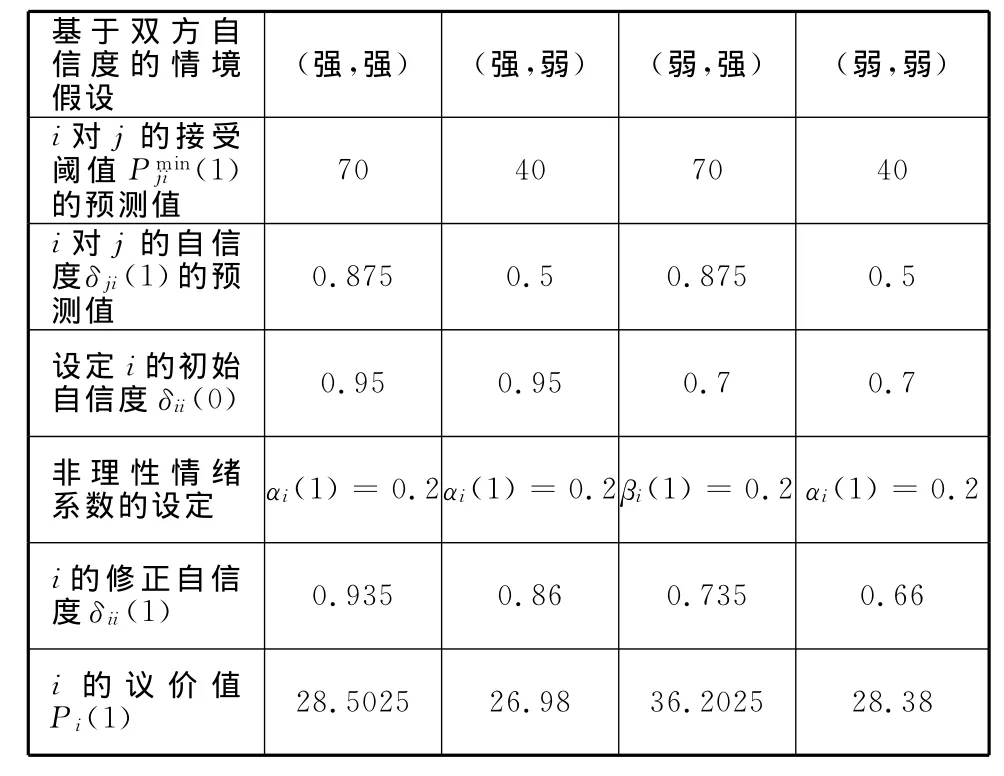
基于双方自信度的情境假设（强，强） （强，弱） （弱，强） （弱，弱）i对j的接受阈值P min ji （1）的预测值70 40 70 40 i对j的自信度δji（1）的预测值0．875 0．5 0．875 0．5设定i的初始自信度δii（0） 0．95 0．95 0．7 0．7非理性情绪系数的设定 αi（1）＝0．2 αi（1）＝0．2 βi（1）＝0．2 αi（1）＝0．2 i的修正自信度δii（1） 0．935 0．86 0．735 0．66 i的议价值Pi（1） 28．5025 26．98 36．2025 28．38

从上表可知，当局中人j认为局中人有较高自信度时，会认为其接受阈值较为接近其报价，则设Pminji（1）＝70，否则设为Pminji（1）＝40；当局中人i自信度较高时，设其初始自信度为δii（0）＝0．95，否则设为δii（0）＝0．7；当局中人i认为其自身与局中人j自信度水平相当或者自身自信度高于对方自信度时，表现出对抗情绪，即此时仅有αi（1）存在，设αi＝0．2，而当局中人i认为自身自信度低于对方时，表现出合作情绪，即此时仅有βi（1）存在，并设βi（1）＝0．2。根据上述假设可运算得出i的议价值Pi（1），从结果中可得出，当局中人i认为其自身自信度高于对方自信度时，即（强，弱）组合，其报价让步幅度是最小的；当局中人i认为双方自信度水平相当时，报价让步幅度水平相近；而当局中人i认为其自身自信度低于对方自信度时，即（弱，强）组合，其报价让步幅度是最大的，这一结果基本符合实际纠纷案例。

同理可知，局中人j将在不同情境下给出自己的议价值，直到一方报价在自己的接受阈值范围之内，议价过程结束。

而在本案例中，由于拆迁方有着相关制度政策的支持，其自信度极高，可视为δii＝1，所以在任何一次议价过程中都不会做出任何让步，最终罗保根一家不得不将自身的接受阈值调整至26万元，方达成一致，纠纷结束。这一案例虽具有一定特殊性，但也验证了该模型的合理性。

五 结论

信息不对称条件下拆迁纠纷动态议价模型针对现实拆迁纠纷问题中的普遍特点，在原有鲁宾斯坦讨价还价模型的基础上做出了一定的完善，案例的演算与分析也验证了该模型中相关因素对当事人议价的设定有直接影响。然而，该模型的构建不仅仅是用于解释既有拆迁纠纷问题，而是试图利用该模型预测在未来开展拆迁工作中可能会遇到的议价纠纷。在拆迁工作开展的过程中，制度政策、经济利益以及当事人之间的信任程度等因素都直接影响议价模型中的各个因素。这也就意味着在开展拆迁工作的过程中，可以通过对上述因素的调整与修正来实现影响议价纠纷的目的，这也便是构建信息不对称条件下拆迁纠纷动态议价模型的现实意义。而如何构建各个因素定制的指标体系，进一步强化定量计算的准确性，也是本研究有待进一步完善的方向。

［1］户邑，刘贵文，彭小兵．城市拆迁管理的博弈分析［J］．重庆建筑大学学报，2005，（5）．

［2］ERIE M S．Property Rights，Legal Consciousness and t he New Media in China：The Har d Case of t he“Toughest Nailhouse in History”［J］．China Infor mation，2012，（1）．

［3］彭小兵，谭蓉，户邑．城市拆迁纠纷的博弈分析及对策建议［J］．重庆大学学报（社会科学版），2005，（5）．

［4］李钟书，翁里．论城市拆迁中社会利益和经济利益的博弈［J］．安徽大学学报，2004，（4）．

［5］钟蔚．城市化进程中征地利益博弈的冲突行为分析与公共治理思路［J］．现代经济探讨，2013，（4）．

［6］朱念劬．拆迁补偿中的多阶段博弈模型研究［J］．中国房地产，2013，（6）．

［7］纪淑娟，张纯金，梁永全，刘宝华．一次性双边讨价还价中参与者让步动机的理性分析与验证［J］．中国管理科学，2013，（S2）．

［8］NASH J F，Jr．The Bar gaining Proble m［J］．Econo metrica，1950，（2）．

［9］Ariel Rubinstein．Perfect Equilibriu m in a Bargaining Model［J］．Econo metrica，1982，（1）：97－109．

［10］OMOTOT，KOBAYASHI K，ONISHI M．Bargaining Model of Construction Dispute Resolution［C］／／Systems，Man and Cyber netics．IEEE Inter national Conference，2002．

［11］郑鸿．征地补偿安置讨价还价博弈分析［D］．福州：福建农林大学，2012．

［12］向钢华，王永县．一种不完全信息相互威慑讨价还价模型［J］．运筹与管理，2008，（6）．

［13］LA MBERT R A，LEUZ C，VERRECCHIA R E．Inf or mation Asy mmetr y，Infor mation Precision，and the Cost of Capital［J］．Review of Finance，2012，（1）．

［14］LAUERMANN S．Dynamic Matching and Bargaining Games：A general Approach［J］．American Econo mic Review，2013，（2）．

［15］周筱莲，庄贵军．讨价还价的博弈模型及其现实补充［J］．西安财经学院学报，2011，（3）．