某直角坐标载运机器人振动特性有限元分析

刘天宋,徐彤彤,帅伟

(1.常州刘国钧高等职业技术学校机电工程系，江苏常州213000；2.盐城工学院工程训练中心，江苏盐城224051)



某直角坐标载运机器人振动特性有限元分析

刘天宋1,徐彤彤2,帅伟1

(1.常州刘国钧高等职业技术学校机电工程系，江苏常州213000；2.盐城工学院工程训练中心，江苏盐城224051)

某直角坐标载运机器人是面向职业教育类教学和竞赛而研制的机器人，其外形如图1所示。由于各种原因，该机器人行驶、取物和堆垛过程中，机身会产生不同幅度的振动。一方面，振动会降低机械手工作的精度；另一方面还会造成机身的共振或疲劳，从而影响整机的寿命。为了进一步提高该产品的性能，需要了解该产品的振动特性，对该产品进行模态分析[1]。

模态分析可用于确定设计结构或机械部件的振动特性，即固有频率和振型。通过模态分析，可以找到机械系统的薄弱模态和主振部件，并提出结构改进意见[2]。工程中常用的模态分析方法有有限元法[3-4]和实验模态分析法[5]2种。相对来说，有限元法操作起来较为方便。随着计算机技术的发展，有限元法在模态分析中占有越来越重要的地位。

本文利用有限元法对该机器人的振动特性进行了研究。先在Pro/Engineer中建立了机器人的几何模型，然后将其导入到Workbench软件中，建立有限元模型，通过模态分析，得出了机器人振动特性的主要振型，并分析了各阶振型的特点，据此总结了机器人在运行过程中应该注意的问题，提出了相应的结构改进方案。

图1　某直角坐标载运机器人

1直角坐标载运机器人的几何建模、功能和参数

该直角坐标载运机器人的结构比较复杂，如图1所示。为了便于建模和减少后续有限元计算中的工作量，在建模时主要对一些主要的结构进行了建模，而将电机、电路板、线槽和同步带等一些次要部件忽略，将其质量折算到其他相应部件中。

图2为采用Pro/Engineer建立的该机器人CAD简化模型。该模型主要由轮胎、底盘、前后梁、左右梁、升降梁、抓取部位等主要结构构成，其中前后梁、左右梁、升降梁和抓取部位构成直角坐标机械手。采用虚拟装配技术将以上各个部位装配在一起。

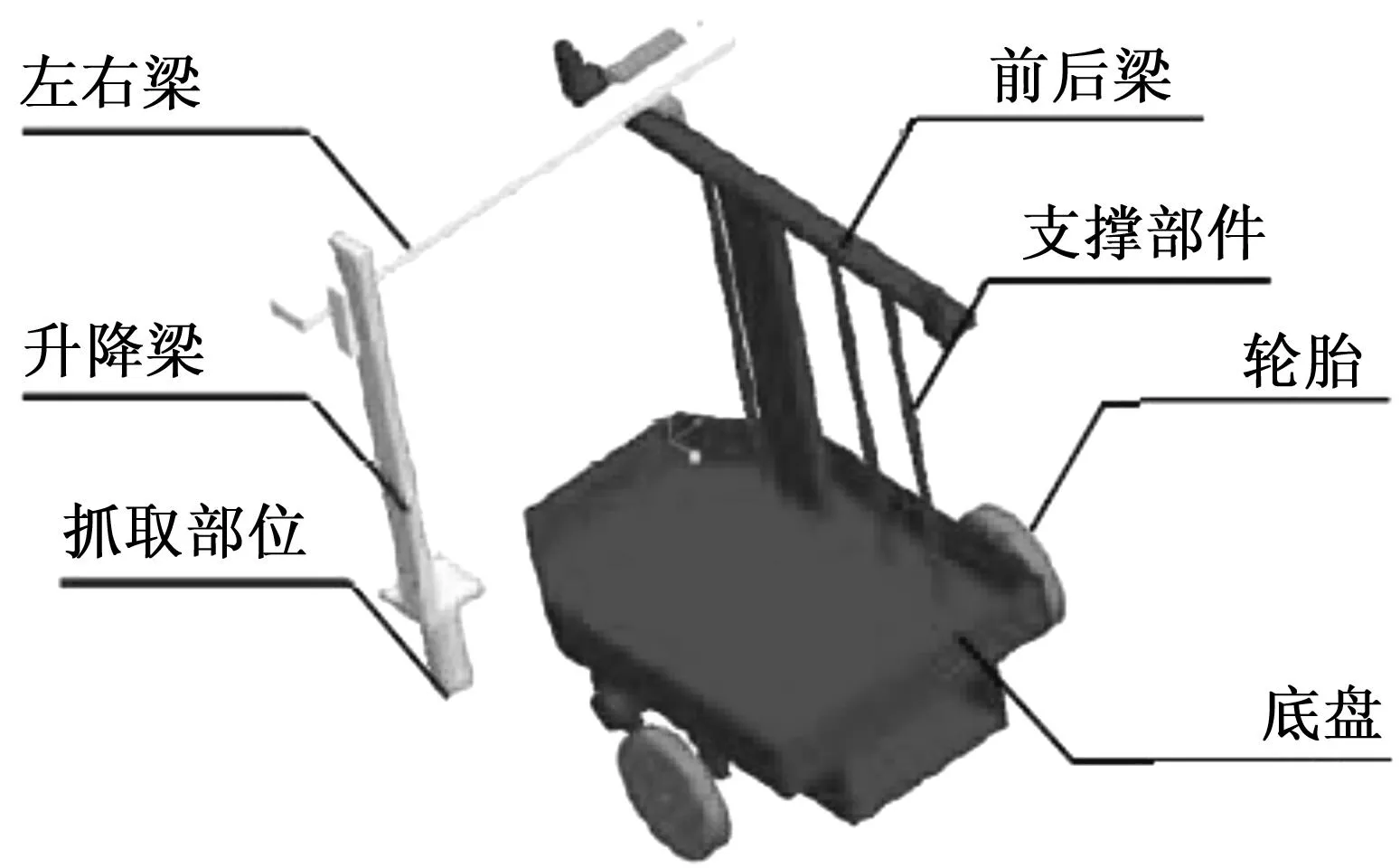
图2　机器人的CAD简化模型

该机器人的主要功能如下：

1)移动到指定位置。机器人底盘上安装有3个轮胎，其中后侧2个轮胎通过联轴器与行走直流电机联接，为驱动轮，前端的1个轮胎为万向轮。

2)取物和堆垛。图中的左右梁可以在步进电机驱动下，通过同步带传动在前后梁的轨道上前后滑动。左右梁也可以在步进电机的驱动下，通过同步带传动沿着左右方向滑动。升降梁可以在步进电机的驱动下，实现升降。抓取部位安装有抓取电机，用来取物和堆垛。

表1给出了该机器人的主要工作参数。

表1　机器人主要工作参数

2有限元模态分析

2.1　有限元模型的建立

将该机器人CAD模型导入ANSYS有限元分析软件中。由于该机器人所采用的材料主要为45号钢，在有限元分析中设置的材料属性如下：弹性模量E为210 GPa，泊松比μ为0.3，密度ρ为7 800 kg/m3。机器人工作时，在地面上移动，因此需要约束机器人3个轮子竖直方向的位移。采用SOLID45单元划分网格，如图3所示。

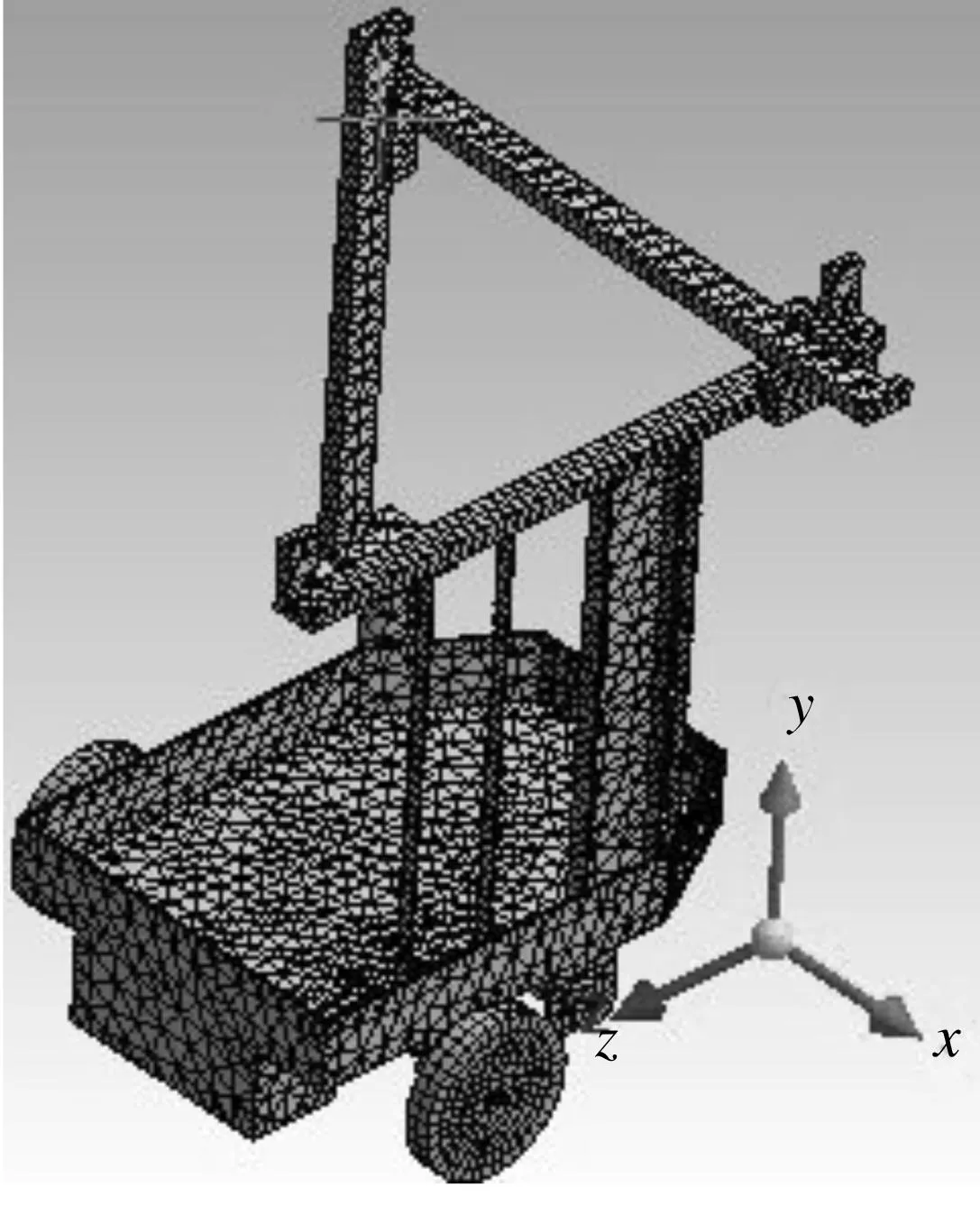
图3　机器人有限元模型的网格划分

2.2　模态计算及结果分析

通常，结构发生共振的频率主要处于低频阶段，因此计算出前6阶模态基本上能够满足对机器人振动特性的研究要求[6]。表2列出了计算得到的机器人各阶模态频率。

表2　机器人的各阶模态频率　Hz

结合表2和计算结果可以总结出以下结论。

1)机器人的1~2阶模态主要表现为xOz平面内的移动，3阶模态表现为绕着y轴的转动。这是由于在机器人底部3个轮胎上施加了y方向的位移约束所致。机器人的4~6阶模态主要表现为支撑部件和机械手的弯曲摆动或扭曲摆动，频率不同时，各个部件的振动方向不同，如图4~6中的应变云图所示。

2)图4为4阶模态的应变云图，图中黑色的框线表示机器人静态时的位置。从图中可以看出，4阶模态振型主要表现为支撑部件和左右梁的弯曲摆动。

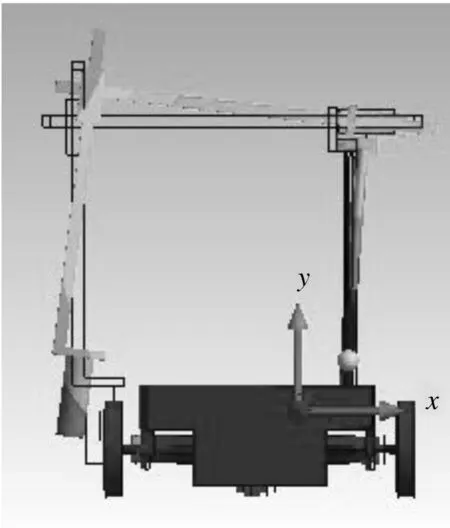
图4　机器人4阶模态振型

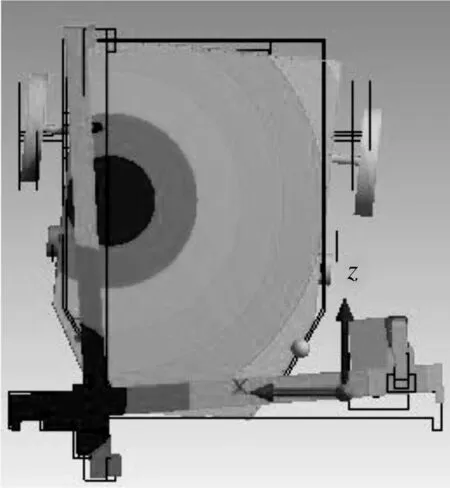
图5　机器人5阶模态振型

图6　机器人6阶模态振型

3)机器人的第5阶振型表现为机械手和底盘绕y轴的摆动。图5表明，底盘位移方向为z轴的负方向，而机械手位移方向为z轴的正方向，因此支撑部件内部将会产生较大的应力。

4)图6为第6阶模态振型。该阶振型同样表现为支撑部件和左右梁的弯曲摆动，但与第4阶模态产生的弯曲摆动方向相反。

5)从各应变云图来看，机器人的支撑部件受各阶模态影响均发生不同程度的变形，是整机较为薄弱的结构环节之一。在下一步的工作中，可以适当对此部位进行结构改进，例如可以通过改变支撑筋的尺寸或者形状，以优化结构的振动特性。表3列出了计算得到的支撑筋直径与机器人各阶频率的关系。从表中看出，支撑筋的频率随着直径的增加而呈现增加的趋势。

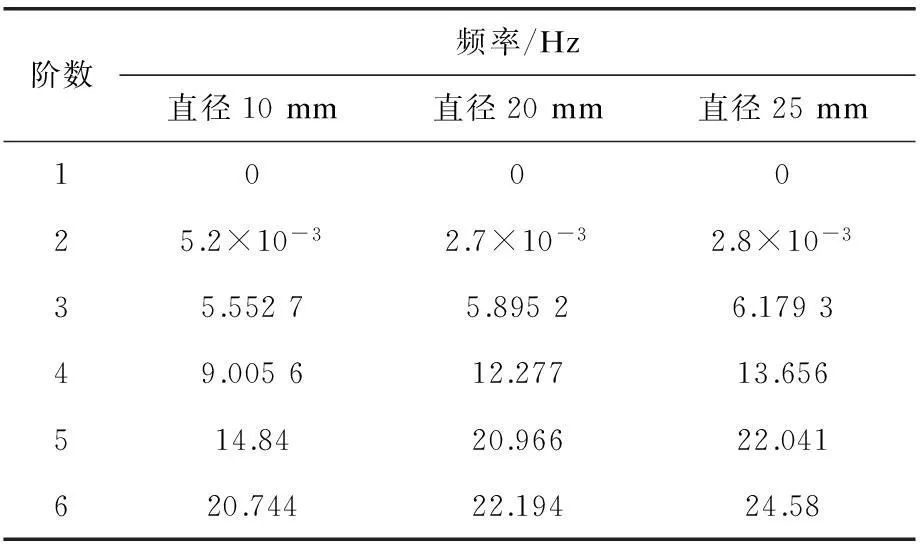
表3　机器人各阶频率与支撑筋模态的关系

综上所述，机器人的1~6阶模态主要表现为支撑部件和机械手的弯曲摆动或扭曲摆动，频率不同时，各个部件的振动方向不同。从以上的分析来看，机械手部位受前6阶模态频率的影响较大，这除了会影响机器人抓取物件的精确度外，还会影响相关零部件的使用寿命。例如，在使用机器人的过程中发现，支撑部件与底盘连接处经常出现螺栓松动的现象，导轨出现不同程度变形或者磨损等问题。此外，从各阶模态对应的应变云图来看，车轮部位受前6阶模态的影响不大。

3结论

机器人整机振动特性取决于其固有频率和振型。通过以上对振动特性的分析，总结了机器人在运行过程中应该注意的问题，并提出了结构改进的一些建议。

1)该机器人在工作中，采用了多个直流电机。通过计算得到，行走电机的频率范围为0~41.67 Hz。步进电机的频率范围为6~18 Hz。而从模态分析结果来看，机器人前6阶模态频率较低，为0~20.74 Hz。显然，电机的工作频率与机器人的低阶频率接近。因此，在实际工作过程中，应该尽量调高电机转速。在改善机身结构工作时，要尽量提高机器人的固有频率，让电机的工作频率远离整机的前几阶模态频率，避免产生共振造成结构的破坏或者影响工作精度。

2)文中以支撑筋的直径变化为例，探讨了机器人的模态频率和支撑筋直径大小之间的关系，并不代表其他部位的结构不需要进行改进。例如，机械手的左右梁可以近似看成力学上的悬臂梁模型，其静态时的变形和动态特性会影响抓取工件时的精度，可以考虑增加加强肋等结构。另外，机器人的高度相对于其长宽尺寸来说较大，这可能也是影响模态的原因之一，需要进一步计算长宽高比例对机身模态的影响。今后将对以上提到的各个部位进行研究，为改进机器人的动静态特性提供依据。

[参考文献]

[1]石广丰,倪坤,史国权,等.基于ANSYS Workbench的激光打孔机模态分析[J].长春理工大学学报,2010(4):95-97.

[2]程丽,刘玉旺,骆海涛,等.165 kg焊接机器人有限元模态分析[J].机械设计与制造,2012(1):147-149.

[3]赵增奎,陆建辉,刘玲.某型号注塑机械手的有限元数值分析[J].机械强度,2005,27(6):803-807.

[4]陈贺.高速压力机动态优化设计[D].南京：东南大学,2010.

[5]权龙哲,佟金,曾百功,等.玉米根茬收获系统的有限元模态分析与试验[J].农业工程学报,2011,27(11):15-20.

[6]杨志敏,周健,李立君,等.基于ANSYS Workbench的采摘机器人臂架模态分析[J].农机化研究,2013(12)：56-58，62.

责任编辑：陈亮

摘要：为了减小某直角坐标载运机器人工作时的振动，运用ANSYS有限元软件对机器人进行了模态分析，求出了表征机器人振动特性的6阶振型、固有振动频率和相应的应变云图，分析了各阶振型的特点及其对机器人结构的影响。根据计算结果，总结了机器人在运行过程中应该注意的问题，并提出了相应的结构改进方案。

关键词：直角坐标机器人；振动特性；模态分析；有限元法

A Modal Analysis of a Cartesian Carrying Robot′s VibrationLIU Tiansong1，XU Tongtong2，SHUAI Wei1

(1.Department of Mechanical and Electrical Engineering,Changzhou Liu Guojun Vocational Technology College,Changzhou 213000;

2.Engineering Training Center,Yancheng Institute of Technology,Yancheng 224051)

Abstract：In order to reduce vibration by a cartesian carrying robot at work,the finite element software ANSYS was used to execute modal analysis.The main six order vibration modes,natural vibration frequency and the corresponding strain contours have been obtained.The characteristics of various order vibration modes and their influences on the robot structure have been analyzed.According to the calculation results,problems to be noted in the process of running were summarized,and corresponding structural improvements were proposed.

Key words：cartesian robots;vibration performance;modal analysis;finite element method

中图分类号：TH113.1

文献标志码：A

文章编号：1671- 0436(2015)05- 0038- 04

作者简介：刘天宋(1988—)，男，硕士，助教。

收稿日期：2015- 06- 01

doi:10.3969/j.issn.1671-0436.2015.05.009