保形动网格策略在CFD/CSD耦合中的应用
2015-02-22陈浩徐敏谢亮康伟
陈浩, 徐敏, 谢亮, 康伟
(西北工业大学 航天学院, 陕西 西安 710072)
保形动网格策略在CFD/CSD耦合中的应用
陈浩, 徐敏, 谢亮, 康伟
(西北工业大学 航天学院, 陕西 西安710072)
摘要:提出了一种基于有限元插值投影,径向基函数(RBF)和无限插值(TFI)的保形动网格策略,并将其用于考虑舵偏扰动的舵身组合体CFD/CSD耦合分析。研究思路为:首先采用RBF方法完成刚性运动组合体投影基面的弹性变形;其次采用基于有限元插值的投影方法按照点、线、面的顺序将上一步的物面网格向投影基面投影,获得变形后的物面网格,期间通过TFI技术保持原始网格的分布;再采用TFI技术将物面网格的变形均匀地插往全场网格,获得最终的全场网格;最后通过CFD/CSD松耦合策略配合耦合边界条件实现耦合计算。通过算例获得的主要结论有:(1)在刚性舵偏16°的算例中,保形动网格策略实现了组合体物面点保形率100%;(2)在考虑舵偏扰动的舵身组合体算例中,保形动网格策略在保持了弹身和舵面几何形状的同时,还保持了合理的网格分布,而总计算时间仅增加2.1%。
关键词:气动弹性;保形;网格变形;有限元方法CFD/CSD耦合;操纵面
在气动弹性和流固耦合这类问题的分析中,由于结构外形在外部气动力的作用下发生了变形,这就需要采用某种方法根据结构表面的变形使气动网格中的空间节点做出相应调整,即所谓的动网格方法[1]。如何提高动网格方法的计算效率和通用性正是目前研究的热点。
在动网格领域,常用的方法有无限插值法(TFI)和径向基函数法(RBF)。传统的TFI方法一般仅能用于结构化网格,但计算效率高,能够支持中等程度的变形。虽然国内学者对TFI方法的缺点进行了诸多的改进[1-2],该方法也在很多问题中得到了应用[3-4],但在三维算例中,要么弹身为方形截面[3-4],要么根部无变形[1-2]。即这些改进依然没有解决一般截面弹身组合体仅舵面变形的问题。最近出现的径向基函数法(RBF)在用于网格变形时,有着通用性好,容易编程实现和在变形连续时对原始网格的正交性保持性好的优点,从而在数值计算中得到了应用[5-7]。但是,文献[7]中仅考虑了舵面的刚性运动,尚未考虑舵面同时存在刚性运动和弹性运动时的动网格策略。
综上所述,目前常用的动网格技术都不能解决舵身组合体只有舵面运动,且同时发生刚性和弹性运动时的网格变形问题。其根本原因在于传统的动网格方法无法保持运动后的组合体几何外形:即使对于单个舵面这样的简单外形,由于实际计算过程中往往通过设置对称面边界进行半模计算以减少计算量,而原始的RBF和TFI方法无法保持对称面位置。如不引入新的方法,单纯的RBF方法、TFI方法或是RBF和TFI结合的方法必然会至少破坏一个部件(翼面/舵面/弹身/机身)的几何外形,甚至会将结合部位的各部件几何外形全部破坏掉。仅仅在极少数的情况下(弹身为方形截面或运动部件的根部不变形),才能保持组合体的几何外形。
为了解决该问题,本文采用有限元插值投影来保持运动后的组合体外形,并结合RBF和TFI动网格方法,形成保形动网格策略(SPGDM),然后将其应用于CFD/CSD耦合气动弹性分析系统中,计算了舵身组合体(弹身为圆形截面)中舵面在同时考虑刚性运动与弹性运动时的动响应。
1保形动网格策略
较新的RBF动网格方法[5-7]与传统的TFI动网格方法[1-4,8]已经在许多气动网格发生刚性/弹性变形的问题中得到了应用。但是这2种方法要进一步应用于复杂外形的气动网格变形则还存在各自的问题。
而本文提出的保形动网格策略通过将目前已有的成熟技术(基于有限元插值的投影技术,RBF插值技术和TFI动网格技术)有机地结合起来,以可以接受的计算效率,来解决组合体外形非定常CFD网格变形中的几何外形保持问题。针对原始物面变形不连续这一本质问题,采用合理的投影策略来获得连续的物面网格变形。其中,RBF插值的实现见文献[9],径向基函数选择Wendland’s C2函数[9],采用贪心算法进行选点;TFI动网格的实现见文献[2]。
由于本文采用的基于有限元形函数的曲面插值有其特殊的处理步骤,故将其与本文提出的保形动网格策略分别进行介绍。
1.1基于有限元形函数的曲面插值
本文所采用的有限元插值,借鉴了文献[10]和文献[11]中等参单元逆变换的思想,采用数值迭代算法获得当地坐标,然后进行物理量的正向插值。
对一般的三维等参单元来说,坐标变换就是将各单元从整体坐标系x-y-z下变换到当地坐标系ξ-η-ζ下。其显式正变换为:
(1)
(2)
(3)
式中,xi,yi,zi为单元中第i个节点的位置坐标,n为单元的节点个数,Ni为第i个节点对应的形函数,x,y,z为插值点处的位置坐标,ξ,η,ζ为插值点处的当地坐标。一般物理量u拟采用与坐标变换相同的函数来进行插值:
(4)
式中,ui为单元中第i个节点处的物理量。
虽然(7)式~(9)式本身并不复杂,但是由于Ni一般并非ξ,η,ζ的线性函数,其逆变换一般并不存在解析形式。因此需要采用数值迭代算法进行逆变换。令b=(x,y,z)T,α=(ξ,η,ζ)T,则(7)式~(9)式可以表示为:b=f(α)。这是一个3阶非线性方程组,可以采用非线性方程组的迭代方法求解。本文选择牛顿迭代法来求解,具体求解步骤如下:
1) 给定迭代初值α0;
2) 计算第k步的误差向量:ek=f(αk)-b;
3) 如果‖ek‖足够小,则转步骤7);
5) 解线性方程组:JkΔα=ek;
6) 更新迭代值:αk+1=αk+Δα,k=k+1,转步骤2);
7) 结束迭代:α=αk。
求出α(即:ξ,η,ζ)之后,将其代入(12)式就能获得u在另外一套网格节点上的值。

上面给出的逆变换求解方法对于插值点在网格单元内部或者距离并不远的情况下,收敛非常迅速,对本文使用的算例,一般10步之内就能收敛。但是,如果插值点与网格单元相距较远时就不容易收敛。所以,为了保证逆变换求解的正确性和效率,应先确定插值点所在网格单元,具体方法见文献[12]。
1.2保形动网格策略的实现步骤
在实现了上文的RBF技术、基于有限元形函数的插值和TFI动网格方法之后,本文提出的保形动网格策略具体步骤和示意图如下(实线表示CFD网格的物面边界,虚线表示投影基面网格,为保证相贯,投影基面应有适当延伸):
1) 采用RBF方法使投影基面网格发生弹性变形,然后使其发生刚性变形,如图3所示;
2) 采用基于有限元插值的投影方法将上一步的物面网格的边界向各投影基面网格反复投影,直到相贯线位置不再变化,如图4所示;
3) 采用TFI技术将物面网格的边界变形均匀地插到整个物面上,如图5所示;
4) 采用基于有限元插值的投影方法将物面的内点向各投影基面网格投影获得当前步的物面网格,如图6所示。
5) 采用TFI技术将物面网格的变形均匀地插往全场网格,获得当前步的全场网格。
本文实现的保形动网格策略的实际应用效果见3.2.2节。
2CFD/CSD耦合方法
2.1气动力计算
三维可压缩非定常守恒积分形式的欧拉方程[8]为:
(5)
式中,t为时间,Q为守恒变量矢量,Fc为对流通量项,Ω和∂Ω是控制体和其边界。对(1)式采用有限性体积法进行求解;对流通量项Fc采用Vanleer格式计算,该格式在超声速流域的稳定性较好;限制器选用鲁棒性较好的minmod型限制器;时间推进格式采用双时间推进,通过引入子迭代将LUSGS格式的时间离散精度扩展到2阶;边界条件在远场处根据速度方向判断是流入还是流出,流入时赋远场值,流出时由内场做一次外插;在物面处对速度采用无穿透条件,令温度和压强在物面法向梯度为零。
2.2结构动力学求解
气动弹性耦合系统中的结构动力学部分采用模态叠加法求解。模态叠加法本质是将各阶结构模态解耦后的降阶方法。利用模态解耦后的结构动力学方程为:
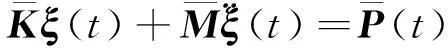
(6)

2.3耦合技术
气动弹性耦合计算采用松耦合策略,如图7所示,主要步骤有:
1) 气动力计算;
2) 将气动力(压强)插往结构网格;
3) 进行结构动力学计算;
4) 将结构变形插往气动网格,并进行网格变形。
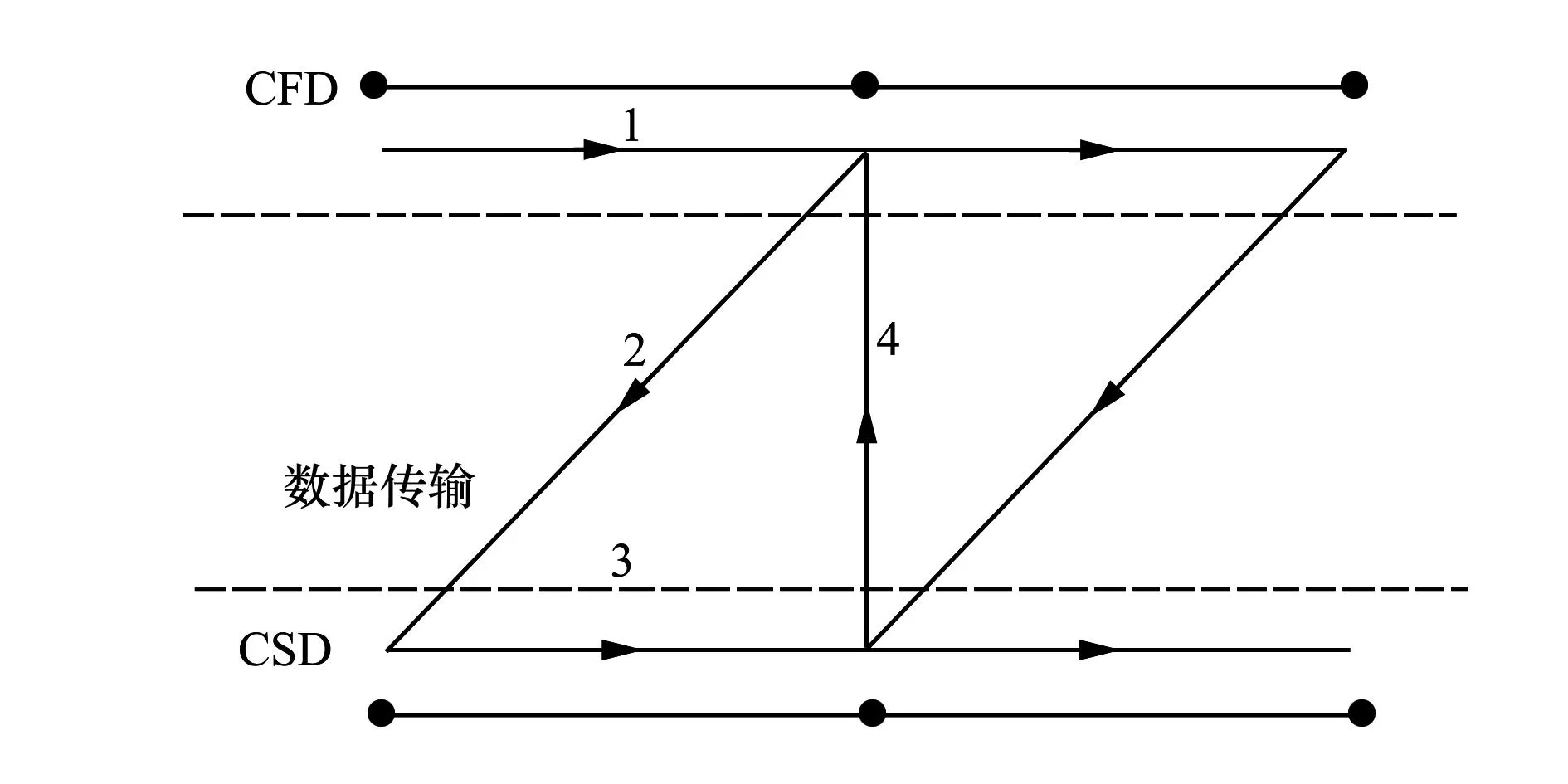
图7 气动弹性耦合示意图
其中,第2步和第4步的插值是在流固耦合边界上进行的(三维问题就是面插值)。在气动系统方面,耦合边界上的速度在边界法向上为零;在结构动力学方面,耦合边界上采用给定压强的边界条件。气动力的插值采用RBF技术,气动网格变形采用本文提出的保形动网格策略予以实现。
3数值计算
为了考察保形动网格策略的保形效果及在CFD/CSD耦合计算中的适用性,以圆截面弹身的舵身组合体为对象进行了16°舵偏和扰动下的动响应计算。其中,气动舵为全动舵,通过舵轴与弹身相连。在对舵身组合体进行CFD/CSD耦合计算时,将弹身考虑为刚性,仅考虑气动舵本身的弹性效应。
3.1模型描述
3.1.1几何外形及气动网格
气动舵的翼型为双弧形,相对厚度为0.05;平面形状为梯形,根弦弦长0.8m,梢弦弦长0.36m,前缘后掠角34.02°。舵身组合体为半模,图8中给出了组合体的的网格拓扑和物面网格。全场网格共21个块,单元总数为373 480。
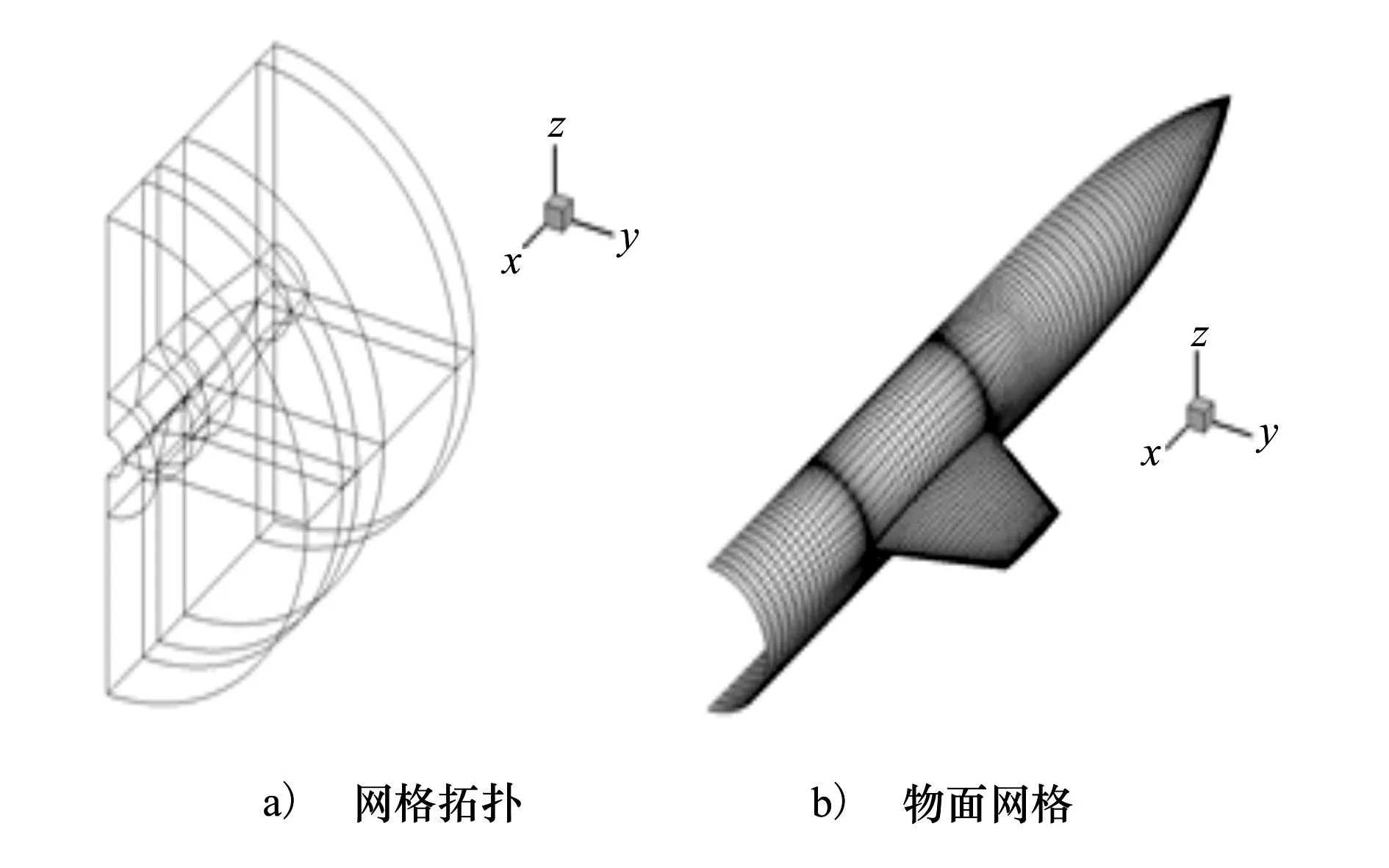
图8 舵身组合体气动网格
3.1.2结构模型
气动舵的结构模型如图9所示。该气动舵由舵面和舵轴组成,舵面和舵轴的材料参数见表1,舵面采用实体单元进行建模,舵轴采用半径为10mm的圆截面梁进行建模。舵轴位于舵面根部1/2弦线处。在舵轴根部加载固支约束,在舵轴与舵面相连的节点通过RBE2与周围8个点相连。

图9 气动舵结构网格

部件E/GPavρ/(kg·m3)舵面700.332800舵轴2200.374480
3.1.3保形所需的投影基面
为了在舵身组合体的耦合计算中保证弹身和舵面的几何外形都不被破坏,本文采用了保形动网格策略,其中所需的投影基面如图10所示。
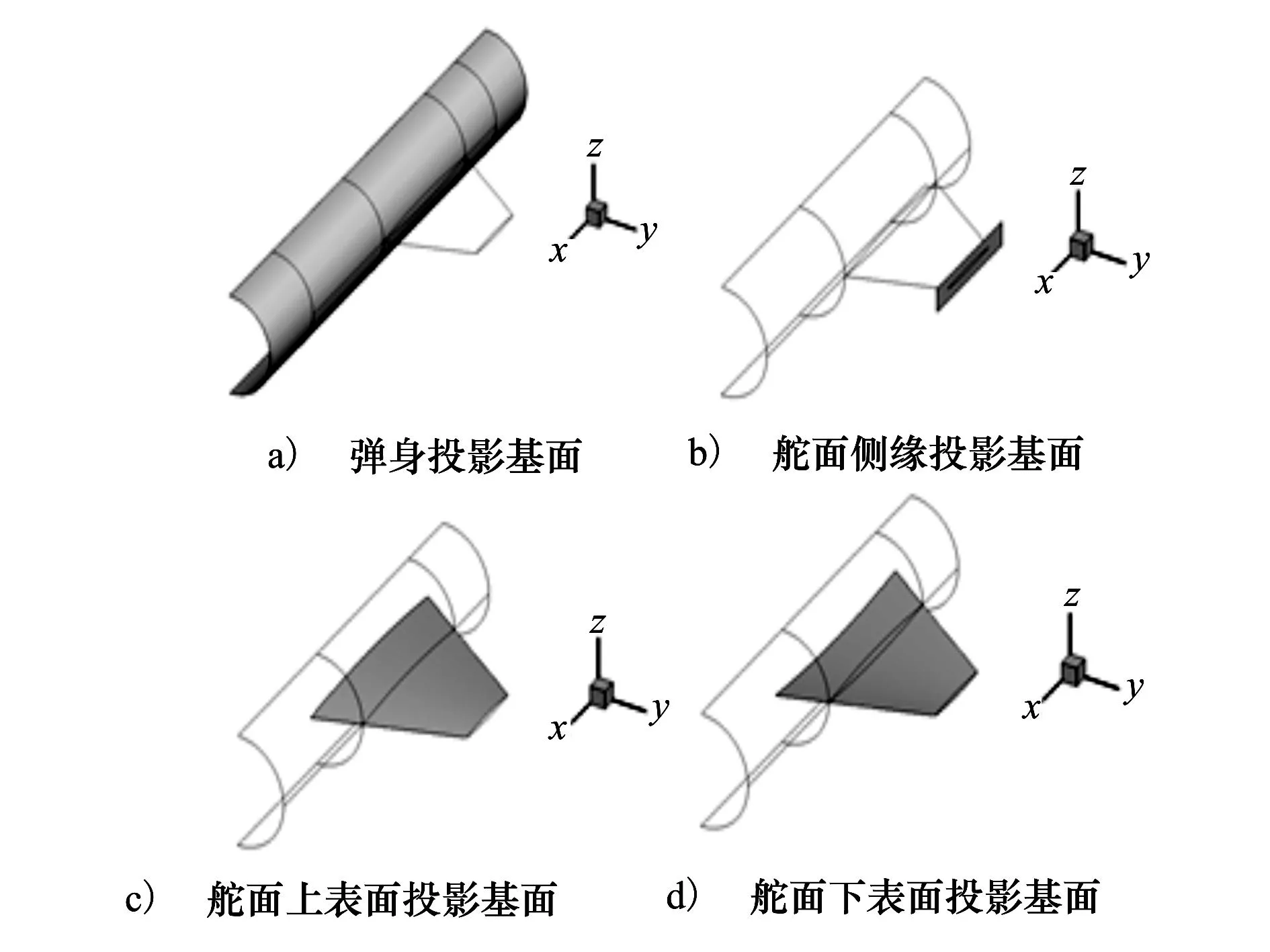
图10 投影基面网格
3.2计算结果
3.2.1结构模态
采用Nastran计算获得气动舵的前4阶结构模态,其中:1阶模态为舵轴弯曲模态,2阶模态为舵轴扭转模态,3阶模态为舵面弯曲模态,4阶模态为舵面扭转模态。从图11中可以看出,舵轴模态的频率要比舵面模态的频率低得多:舵轴模态频率不超过60Hz,舵面模态的频率不低于299Hz。这说明舵轴刚度要远小于舵面刚度。
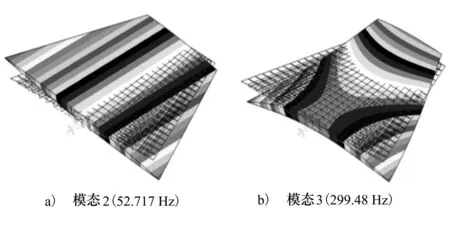
图11 舵面结构模态
3.2.2动网格效果
对舵面施加16°的舵偏,采用常规TFI方法,保持舵面形状不变,获得变形后的网格如图12所示。

图12 TFI方法所获得的组 图13 保形动网格策略获得 合体变形后网格 的组合体变形后网格
从图12中可以看到,由于舵面变形的拖拽效应,导致弹身发生了巨大的变形,而这种变形在实际导弹舵偏时完全不存在。由表2知变形后的弹身网格仅有7.06%的网格点位于真实的弹身上。采用图12中的气动网格进行定常CFD计算(Ma=2,H=3km)所获得的压力系数如图14所示,从图14可以看出,由于弹身被拉坏,产生了非物理的压缩区和膨胀区。可想而知,在组合体的CFD/CSD耦合分析中采用常规TFI方法必然会造成巨大的误差,结果的可信度将非常有限。

表2 弹身节点保形效果
而采用保形动网格策略,在舵偏16°时,可同时保持舵面和弹身形状不变,变形后的网格如图13所示。在这一过程中所使用的4个投影基面网格如图10所示,为了保证投影的精度,这些投影基面都采用了8节点四边形单元。为了考察保形动网格策略是否有效,表2给出了弹身节点的保形效果,从表中可以看出气动网格弹身节点在变形之后100%保持在了弹身上。从图13中可以清晰地看出,采用了保形动网格策略之后,在常规TFI方法中巨大的弹身变形得以完全避免。从图15中可以看出由于变形之后的弹身网格依然维持了原始外形,因此没有产生非物理的压缩区和膨胀区,从而说明保形动网格策略能够保持组合体的CFD/CSD耦合分析的可信度。

图14 TFI变形后Cp云图 图15 SPGDM变形后Cp云图
3.2.3CFD/CSD耦合结果
采用本文的CFD/CSD耦合方法,在Ma=2,H=3 km的来流状态下,对舵身组合体进行扰动下的动响应分析。CSD部分采用3.2.1节中计算出的前4阶结构模态。耦合时间步长取为0.0001 s,内迭代步数为50步。气动舵上加载的舵偏扰动为:δ(t)=Δδasin(2πωt)。其中,Δδa=2°,ω=40 Hz。
表3中给出了在1个非定常耦合时间步内,不同动网格方法计算时间(计算机CPU主频3.4GHz,内存2G)的对比。

表3 计算时间对比
从表3中可以看出,虽然保形动网格策略本身的计算时间(0.73s)相对TFI方法(0.05s)大大增加,但在单个CFD/CSD耦合时间步内仅使计算时间(32.92s)增加了0.68s,不到总时间的2.1%。考虑到保形策略能保证耦合分析的可信度,仅增加2.1%的计算时间完全可以接受。
为了考察该种扰动下的气动弹性效应,特别设置2个算例:case1中来流状态为Ma=2,H=3km,case2则忽略外界气流的影响,仅考虑结构本身在扰动激励下的响应。两算例各阶模态广义位移的对比如图16所示。
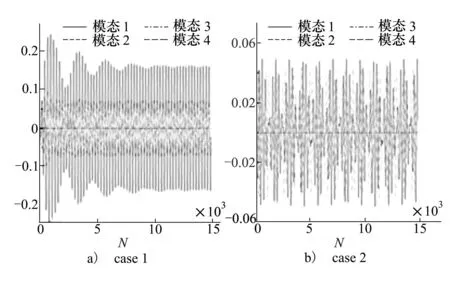
图16 广义位移响应对比

图17 典型时刻物面网格变形示意图
从该图中可以看出,case1和case2的响应主要位于1阶模态和2阶模态上;但由于气动和结构的耦合效应,case1的广义位移振荡幅值远超case2,并且幅值随时间衰减,在达到动稳定之后,1阶模态和2阶模态的振荡幅值分别是case2的3.2倍和1.75倍。
为了考察保形动网格策略在组合变形下的效果,特别选择case1中t=0.105s(N=1 050,刚性舵偏角为1.8°,各阶广义位移为0.238,0.073,-0.591×10-3,0.174×10-4)和case2中t=0.356s(N=3 560,刚性舵偏角为2°,各阶广义位移分别为-0.022,0.043,-0.102×10-6,-0.155×10-5)这2个典型时刻,其物面网格变形如图11所示。从图17中可以看出,在气动弹性耦合效应下,case1的变形远大于case2;即使在case1如此巨大的变形之下,保形动网格策略依然保证了弹身和舵面的几何形状不被破坏,同时还保持了原始网格上较为合理的网格分布。
4结论
本文结合RBF技术、基于有限元形函数的插值和TFI动网格方法,形成了能够同时考虑刚性变形与弹性变形的保形动网格策略并将其应用于舵身组合体CFD/CSD耦合计算中。通过计算分析,获得结论如下:
1) 通过使舵身组合体刚性舵偏16°,验证了本文提出的保形动网格策略能够避免常规TFI方法导致的巨大弹身变形,实现了100%的保形率,从而没有产生非物理的压缩区和膨胀区,说明保形动网格策略能够保证组合体的CFD/CSD耦合分析的可信度。
2) 在舵身组合体CFD/CSD耦合计算中发现,采用保形动网格策略仅使单个非定常步内总时间(32.92s)增加了0.68s,不到总时间的2.1%,其计算效率可以接受。
3) 在Ma=2,H=3km的来流和振幅为2°频率为40Hz舵偏扰动的共同作用下,舵身组合体气动弹性效应明显,其1阶模态和2阶模态的广义位移幅值为无来流时的3.2倍和1.75倍。
(4) 在CFD/CSD耦合分析中产生的组合变形下,保形动网格策略依然保证了弹身和舵面的几何形状不被破坏,同时还保持了原始网格上较为合理的网格分布。
参考文献:
[1]黄礼铿, 高正红, 左英桃. 一种快速稳健的并行多块结构动网格方法[J]. 计算力学学报, 2012,29(3): 363-367
HuangLK,GaoZH,ZuoYT.AFastandRobustParalelizableMovingMeshAlgorithmforMulti-BlockStructuredGrids[J].ChineseJournalofComputationalMechanics, 2012,29(3): 363-367 (inChinese)
[2]张兵, 韩景龙. 带旋转修正的弹簧-TFI混合动网格方法[J]. 航空学报, 2011, 32(10): 1815-1823
ZhangBing,HanJinglong.Spring-TFIHybridDynamicMeshMethodwithRotationCorrection[J].ActaAeronouticaetAstronauticaSinica, 2011, 32(10): 1815-1823 (inChinese)
[3]陈坚强, 陈琦, 袁先旭,等. 舵面操纵动态响应的数值模拟研究[J]. 力学学报, 2013(2): 302-306
ChenJianqiang,ChenQi,YuanXianxu,etal.NumericalSimulationStudyonDynamicResponseunderRudderControl[J].ChineseJournalofTheoreticalandAppliedMechanics, 2013(2): 302-306 (inChinese)
[4]董琳琳. 超限插值法在舵面振荡偏转数值模拟中的应用[J]. 弹箭与制导学报, 2011(4): 207-209
DongLinlin.TheApplicationofTransfiniteInterpolationtoNumericalSimulationofControlSurfaceOscillatingDeflection[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2011(4): 207-209 (inChinese)
[5]谢亮, 徐敏, 张斌,等. 基于径向基函数的高效网格变形算法研究[J]. 振动与冲击, 2013, 32(10): 141-145
XieLiang,XuMin,ZhangBin,etal.SpacePointsReductioninGridDeformingMethodBasedonRadialBasisFunctions[J].JournalofVibrationandShock, 2013, 32(10): 141-145 (inChinese)
[6]谢亮, 徐敏, 安效民,等. 基于径向基函数的网格变形及非线性气动弹性时域仿真研究[J]. 航空学报, 2013, 34(7): 1501-1511
XieL,XuM,AnXM,etal.ResearchofMeshDeformingMethodBasedonRadialBasisFunctionsandNonlinearAeroelasticSimulation[J].ActaAeronouticaetAstronauticaSinica, 2013, 34(7): 1501-1511 (inChinese)
[7]AndreasKM.AircraftControlSurfaceDeflectionUsingRBF-BasedMeshDeformation[J].InternationalJournalforNumericalMethodsinEngineering, 2011, 88: 986-1007
[8]谢亮, 徐敏, 李杰,等. 基于CFD/CSD耦合的颤振与动载荷分析方法[J]. 振动与冲击, 2012, 31(3): 106-110
XieL,XuM,LiJ,etal.FlutterandDynamicAnalysisBasedonCFD/CSDCouplingMethod[J].JournalofVibrationandShock, 2012, 31(3): 106-110 (inChinese)
[9]王刚,雷博琪,叶正寅. 一种基于径向基函数的非结构混合网格变形技术[J]. 西北工业大学学报, 2011, 29(5): 783-788
WangG,LeiBQ,YeZY.AnEfficientDeformationTechniqueforHybridUnstructuredGridUsingRadialBasisFunctions[J].JournalofNorthwesternPolytechnicalUniversity, 2011, 29(5): 783-788 (inChinese)
[10] 包劲青, 杨强, 官福海. 线性等参单元逆变换的几何二分法及其修正[J]. 计算力学学报, 2010, 27(5): 770-774
BaoJQ,YangQ,GuanFH.GeometricDichotomyMethodforInverseIsoparametricMappinginLinearFiniteElementandItsCorrectionMeasure[J].ChineseJournalofComputationalMechanics, 2010, 27(5): 770-774 (inChinese)
[11] 周艳国, 陈胜宏, 张雄等. 改进的等参逆变换算法在耦合场分析中的应用[J]. 岩土力学, 2008, 29(11): 3170-3173
ZhouYG,ChenSH,ZhangX,etal.ImprovedInverseIsoparametricMappingMethodandItsApplicationtoCoupledAnalysis[J].RockandSoilMechanics, 2008, 29(11): 3170-3173 (inChinese)
[12]WangJZ,ParthasarathyV.AFullyAutomatedChimeraMethodologyforMultipleMovingBodyProblems[J].InternationalJournalforNumerialMethodsinFluids, 2000, 33: 919-938
Applying Shape Preserving Grid Deformation to CFD/CSD Coupling
Chen Hao, Xu Min, Xie Liang, Kang Wei
(College of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China)
Abstract:The shape preserving grid deforming method (SPGDM) based on finite element interpolating projection, radial basis function (RBF) and transfinite interpolation (TFI) is proposed and used in the CFD/CSD coupling analysis of rudder-body combination with the rudder-deflection interaction considered. To fulfill this research, firstly, the project base surfaces of combination with rigid deformation are deformed elastically with RBF method. Secondly, solid surface grids are projected to base surfaces in point-line-surface order with the projection method based on finite element interpolation, meanwhile TFI is used to keep the grid distribution. Thirdly, deformed volume grid is obtained by interpolating the deformation of surface grids evenly with TFI method. Finally, the CFD/CSD coupling is achieved after using loose coupling methodology with coupling boundary. The results and their analysis show preliminarily 2 conclusions: (1) in the 16°rudder deflection case, SPGDM fills 100% shape preserving ratio of the combination; (2) in the rudder-body combination case with rudder-deflection interaction, SPGDM not only preserves the geometrical shape of body and rudder but also keeps reasonable distribution of original grid, while the total time increase is only 2.1%.
Key words:aeroelasticity; shape preserving; grid deformation; finite element method; CFD/CSD coupling; control surfaces
中图分类号:V211
文献标志码:A
文章编号:1000-2758(2015)05-0732-07
作者简介:陈浩(1988—),西北工业大学博士研究生,主要从事超声速气动弹性问题、高超声速气动热弹性问题研究。
基金项目:国家自然科学基金(11402212)资助
收稿日期:2015-04-08
