基于熵权模糊综合法的房地产开发风险评价
2015-02-22常珈宁
常珈宁
(西安欧亚学院建筑工程学院,陕西西安710065)
基于熵权模糊综合法的房地产开发风险评价
常珈宁
(西安欧亚学院建筑工程学院,陕西西安710065)
近年来,房地产行业日渐成为我国国民经济发展的支柱型产业,也是我国进行基础性建设的标志性成果。伴随房地产业的发展,房地产开发企业也应运而生并迅速成长。房地产开发因其开发周期长、投资金额大,受众多因素影响等特点,房地产开发工作潜在巨大风险,若不能将其风险控制或引导在可研阶段,开发企业可能将遭受巨大经济损失,并连带产生多种社会不安定因素。本文针对于此,通过建立熵权模糊综合评判矩阵展开了研究。
房地产开发风险;熵权
前言
所谓房地产风险就是指在房地产开发过程当中,有众多因素影响利润的获得,并且这些众多因素凭借个人的主观意识是无法预测和控制的,进而会导致房地产开发企业得不到预期的利润和收获,使得房地产开发企业遭受严重经济损失的概率。目前,对于房地产开发风险的研究不多,并且大多停留在定性分析层面,有很大的主观性,不能客观真实的反映房地产开发存在的风险。本文主要依据熵权模糊综合评价理论,采取定量与定性相结合的分析方法,对房地产开发项目进行深入剖析,科学客观的建立评价指标,对开发风险进行了评价研究,为房地产开发企业风险评价提供了有利工具,很大程度地避免了风险的发生。
一、基于熵权模糊综合法房地产开发风险评价
1、房地产开发风险分析
房地产开发是一个高收入与高风险并存的动态过程。房地产开发具有投资大、地理位置固定、工程建设工期长、众多因素影响的特点,导致房地产开发面临众多不利因素和风险。因此,准确掌握房地产开发风险是构建评价指标和建立评价模型的前提条件,本文通过市场调研以及专家座谈等多种方式,将房地产开发风险归结为以下几个方面。
(1)技术风险
房地产开发如同其他生产企业一样,先进生产工艺、熟练的技术工人以及先进的生产工具都是提高效率、节省成本、赢得市场的核心竞争力。房地产开发企业更是如此,先进的生产工艺、高水平的技术工人以及先进的生产工具势必会提高工程质量、缩短施工工期,树立好的市场口碑。
(2)银行风险
投资金额大、开发周期长是房地产开发的一个显著特点。大多房地产企业获取巨大资金的渠道主要依靠银行贷款,在此分为三种风险。第一、能否顺利贷款。能否顺利贷款取决于开发企业的信用度以及担保额,因此企业需要在平日的生产经营中积累良好的信用度,并储备一定量的担保额,这样才能顺利地取得银行贷款;第二,能否顺利取得足额贷款。银行放款额度是依据具体项目类型、企业资质、企业已建工程等,因此开发企业在此之前要对项目进行准确评估,确保贷款满足开发项目需要;第三,银行利率调整。银行利率的调整受到许多因素影响,高额的贷款利息是开发企业应着重考虑的一项费用,及时掌握银行利率变动趋势,有助于节省开发成本,保证资金流动顺畅。
(3)经营风险
房地产经营,主要是指房地产所有者对房地产开发类型选择、房地产销售、租赁等市场行为。在此存在三种风险:第一,开发类型风险。房地产具有位置固定的特点,因此在合适位置开发适合房地产类型,才能取得最大效益。第二,经营方式风险。房地产经营一般与房地产开发同步,这样有利于快速回收资金,减少贷款利息,增强资金流动活力。房地产经营应该采取多种灵活方式进行,传统的或不结合实际的经营方式往往存在较大的风险,不利于资金回收和流动,使得开发企业面临困境。
(4)经济风险
房地产开发受宏观经济和行业经济的影响。经济景气,市场繁荣,房地产开发风险降低;经济萧条,市场萎靡,房地产开发风险增大。因此在进行房地产开发前要充分预判开发周期内的经济形势,政策导向,尽可能规避由于经济变化所产生的风险。
(5)市场风险
市场风险是指在房地产交易过程当中供需矛盾导致的销售风险。市场风险主要有以下两种类型风险。第一,市场供求关系风险。市场供求关系极大程度影响房地产的销售,市场供大于求则存在产品滞销、降价销售的风险。第二,市场认可度风险。房地产属于特殊商品,受地理位置、环境、朝向、楼层等细节因素影响。房地产开发企业需要对市场进行准确评估,选在适合的区位开发合适的业态形式,提高质量降低成本,不断地打造企业品牌,树立良好的口碑。
(6)政治风险
房地产开发政治风险是指房地产开发受国家政策调控、经济形势影响的风险。国家出台有利政策,社会安全稳定则有利于房地产发展,降低房地产开发风险;国家实施房地产调控政策,限制房地产开发,则会大大增加房地产开发的风险。作为房地产开发企业不但要善于抓住政策机遇,更要学会研判政治形势,在有利的时机进行开发。
(7)自然风险
自然风险是指由于人们对自然力失去控制或自然本身发生异常变化,如地震、火灾、滑坡等,给投资者带来损失的可能性。自然风险是偶发性的随机事件,不受任何人为主观因素的影响,是任何一个房地产开发企业不可避免的,该事件一旦发生房地产开发企业将蒙受不同程度的损失。
2、房地产开发风险指标体系的建立
(1)指标构建的原则
房地产开发风险的评价需要建立全面客观的指标体系,这样才能客观全面的评价风险程度。同时,风险指标体系的建立需要遵循一定原则,这样所建立的指标不但能准确评价风险程度,也具有较强的操作性,归纳起来有三点原则,分别是科学性和简单性原则、全面性和实用性原则、定性和定量指标相结合原则。
(2)房地产开发风险评价指标的选取
综合对房地产开发风险分析和指标构建原则,本文将房地产开发风险分为七种,第一种是技术风险,技术风险包括施工工艺风险、生产工具风险、技术工人风险;第二种是银行风险,银行风险包括贷款风险、利率风险;第三种是经营风险,经营风险包括开发类型风险、经营方式风险;第四种是经济风险,经济风险包括宏观经济风险、行业经济风险;第五种是市场风险,市场风险包括市场供求关系风险和市场认可度风险;第六种是政治风险,政治风险包括政策风险和政治环境风险;第七种是自然风险,自然风险只包括偶发事件风险。
3、熵权模糊综合评价模型
(1)熵的基本原理
熵期初是热力学中的概念,最先有申农C.E.Shannony引入到信息论中,被称之为信息熵。利用熵赋权重是一种客观的赋权方法,在具体使用过程中,熵权根据各指标的变异程度,利用信息熵计算出各个指标的熵权,再通过熵权对各个指标权重进行修正,从而得出比较客观的指标权重。
4、建立熵权模糊综合评价模型
(1)确定风险因素集
因素指标集:将因素集U按其属性分成m个因素指标集{U1,U2…Um},表示因素评价指标体系中第i(1≤i≤m)个指标。
因子指标集:每一个因素指标对应若干个因子指标,即,Ui={Ui1Ui2…Uij…Uik}(j=1,2,…,k),其中:Uij表示对应指标Ui的第j个因子指标,k为对应Ui的因子指标的个数。因子指标后的指标,依此类推。
(2)确定评判对象的评语集
评价集是对各层次因素状态的直接描述和表征方式,可采用等级评价。例如,对某房地产开发项目进行风险评价,分为两级指标,采用五个等级评价各因素,即V={V1V2V3V4V5},评语集V={几乎没风险,存在少许风险,有风险,风险比较大,非常有风险}。
(3)确定指标权重
采用熵值法确定因素层级指标集相应的权重为:w=(w1w2…wm),因子层级指标集相应的权重为:w=(wi1wi2…wik),因子层级指标后的指标集依此类推。
(4)构建模糊评判矩阵
对于每一个评价因子和评价等级之间的关系,可用模糊评判矩阵表示。设从Uij到V的模糊评价矩阵为:
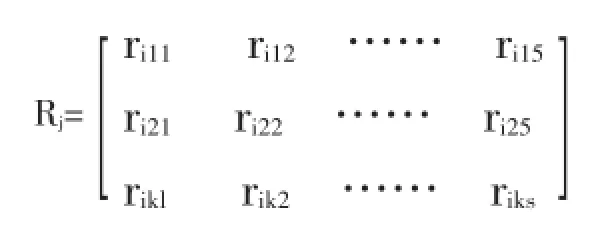
,其中s为评语集元素的个数,rijp表示子因素指标Uij对于第P级评语Vp的隶属度,,表示:对于指标Uij有mijp个Vp级评语(P=1,2,…,s)。
(5)因素层级评价指标的模糊评判
对因子层级指标Uij的评价矩阵Ri作模糊矩阵运算,得到主因素层Ui对于评语集V的隶属度向量Ci,Ci=wi·Ri,Ci= (ci1ci2…cip…cis),其中ci=min{1,p=1,2,…,s)。
(6)因子层级评价指标的模糊评判
由上步得到的主因素层各指标的隶属向量可构成一个总的评价矩阵:
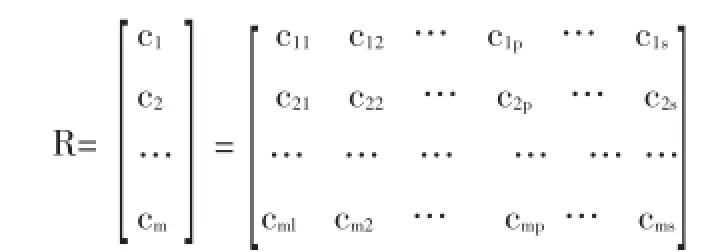
再对其进行模糊矩阵运算,即得到目标层对评语集V的隶属向量C
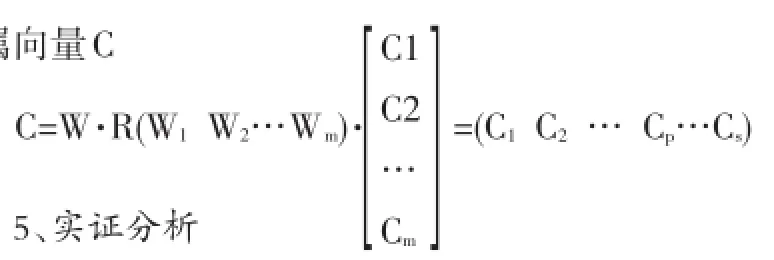
5、实证分析
(1)案例
位于某市东二环以东3公里处有一占地200亩居住用地,该地块前身为一老国有企业,因经营不善转让土地。当年国家实行贷款紧缩政策、为控制房价实施限购政策。试分析该房地产开发企业开发该项目所面临风险程度。
(2)利用熵权模糊综合评价模型进行风险评价
a、确定风险因素集
根据上述理论,结合该项目实际情况,分别邀请该市相关专家对项目开发进行了风险分析,认为主要面临五种风险,分别是:银行风险(包括:贷款风险、利率风险)、经营风险(包括:开发类型风险、经营方式风险)、市场风险(包括:市场供求关系风险、市场认可度风险)、技术风险(包括:施工工艺风险、生产工具风险、技术工人风险)、政治风险(包括:政策风险、政治环境风险)。
b、确定评语集
对于风险因子对应的等级集合,我们按风险程度给出评价等级集为:V=[V1V2V3V4V5]=[风险很小风险小风险一般风险极高风险很高];根据专家小组的意见,给出相应的分值为F=[10 30 50 70 90]。
c、确定指标权重
依据熵权模糊综合评价原理,分别邀请了技术专家、经济专家、项目管理专家、风险分析专家及政府官员组成的专家小组对因素和因子进行重要性评定,构造出判断矩阵。用熵权模型计算得到因素层级和因子层级的权重。
因素层对目标层的权重集合为:
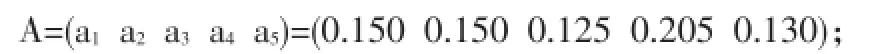
因子层对因素层的权重集合分别为:

(4)构建模糊评判矩阵
由于等级对因子的隶属度评判结果与具体问题有关,依据该项目的实地条件,并结合专家小组对这些资料进行分析评判,对评判结构计算整理后得出评判矩阵如下:


(5)各层级评价指标的模糊评判
一级指标的模糊评价集:
由一级指标的模糊评价集B得到新的模糊评价矩阵,即

进行第二级模糊综合评判:
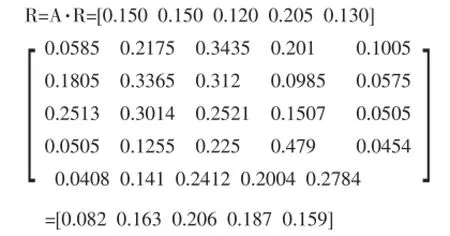
(3)综合评判结果分析
结合评价及对于目标层级的权重综合可得该项目风险程度:
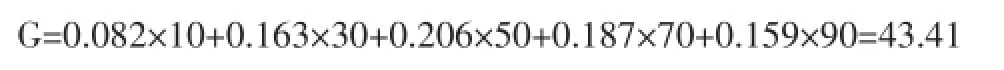
以上分析结果说明该房地产开发项目风险程度一般。由于熵权模糊评价方法综合考虑了风险的各方面因素,得出的结果是对房地产开发项目风险整体上的宏观评价,这一评价结果给房地产开发企业提供了一个信息,即该项目开发风险适中,单从风险角度考虑,投资者可以进行投资;然而从等级对因子的隶属度评判结果中我们可以看出,该项目主要风险在于政治风险导致的一系列问题,因此项目管理者要紧随国家政策,有的放矢。
结论
熵权模糊综合评价法相对于那些主观赋值法,精度较高,客观性更强,能够更好的解释所得到的结果,它是是通过对影响房地产开发风险的各个层面的风险因素进行分析,并把风险程度进行量化的科学评价方法,它能够客观真实的反映房地产开发风险的强度等级。本文将房地产开发风险细化为7个因素层级评价指标和12个因子层级指标,全面系统的反映了房地产开发面临的风险,并利用商权模糊综合评价方法建立了模型,为分析房地产开发风险等级提供了实用工具,为决策者提供了可靠依据,降低了投资风险,为房地产开发的安全运行保驾护航。
[1]胡永宏,贺思辉.综合评价方法[M]北京:科学出版社,2009.
[2]申立银,俞明轩.房地产市场风险[M].天津:天津大学出版社,1996.
[3]蒋泽军.模糊数学教程[M].北京:国防工业出版社,2004: 145-148.
[4]马歇尔.经济学原理[M].北京:商务印书馆,1997: 52-58.
[5]李翔.商业房地产项目投资风险分析与研究[D].重庆大学,2008.
[6]杨福涛.商业房地产投资风险评价及规避研究[D].西北农林科技大学,2008.
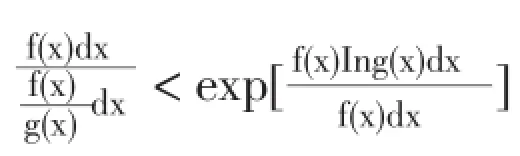
综合1。,2。得结论.
同样的证法可得如下不等式链
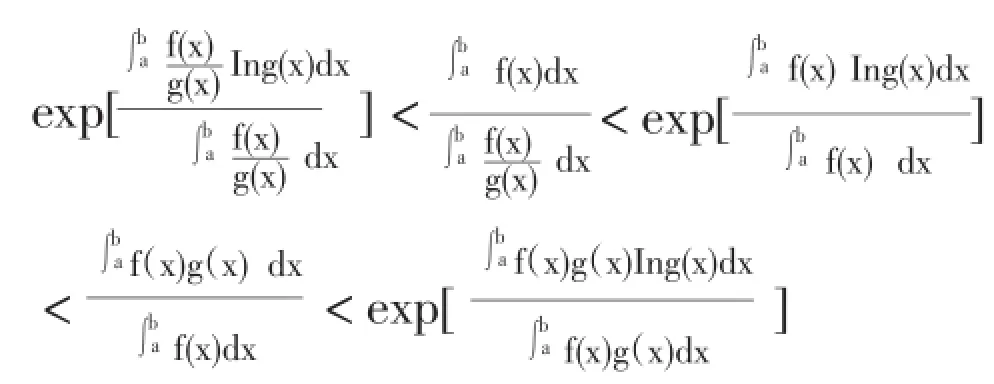
四、小结
全文主要讨论了半严格凸函数的4个性质,研究了它们在不等式证明中的应用,并给出了3个例子。这在一定意义上推广和完善了半严格凸函数,进一步表明了凸函数是特别重要且应用非常广泛的一类函数,有一定的理论意义和应用价值。
参考文献
[1]欧阳光中,姚允龙.数学分析[M].上海:复旦大学出版社, 1993.
[2]严子谦,尹景学,张然.数学分析[M].北京:高等教育出版社,2004.
[3]Ton M.Apostol Mathematical Analysis(Second Edition)[M].London:Addison–Wesley Publishing Company,1975.
[4]史树中.凸分析[M].上海:上海科学技术出版社,1990.
[5]汪林等.数学分析问题研究与评注[M].北京:北京科学出版社,1995.
[6]YANG XM.Semi-st rict ly Convex Function[J]. Opsearch,1994,31(1):15-27.
[7]金洪臻等(译).不可微最优化[M].大连:大连理工大学出版社,1991.
[8]钱吉林.数学分析解题精粹[M].北京:崇文书局,2003.
[9]孙本旺,汪浩.数学分析中的典型例题和解题方法[M].长沙:湖南科学技术出版社,1985.
[10]徐利治,王兴华.数学分析的方法及例题选讲[M].北京:高等教育出版社,1981.
The Characteristics and Applications of Semi-strictly Convex Function
Li Yan
(Yan’an Vocational and Technical College,Yan’an Shaanxi 716000)
Convex function is a kind of important functions,which plays a major role in convex mathematical analysis and mathematical programming,and has a wide range of applications in the fields of inequality proof and other areas.On the basis of Yang Xinmin’s research on the semi-strictly convex function,some properties,inequality proof applications of the upper semi-strictly convex function and the lower semi-strictly convex function are researched.In addition,some examples are given in this paper.
semi-strictly convex function;properties;inequality;app lication
F293.33
A
1674-6198(2015)03-0105-03
2015-03-14
常加宁(1991-)男,陕西米脂人,西安欧亚学院建筑工程学院。
