一类金融混沌系统的广义投影同步
2015-02-22李珍
李 珍
(唐山学院 基础教学部,河北 唐山 063000)
一类金融混沌系统的广义投影同步
李 珍
(唐山学院 基础教学部,河北 唐山 063000)
以一类金融混沌系统为例,提出了一个驱动系统对应多个响应系统的广义投影同步方法,实现了驱动-响应-响应系统之间的同结构广义投影同步,以及三个类型完全不同的混沌系统的异结构广义投影同步。通过改变广义投影同步的比例因子,获得了任意比例于原驱动混沌系统输出的混沌信号,数值仿真验证了此方法的有效性。
金融混沌系统;广义投影同步;比例因子
自从Pecora和Corroll提出混沌同步的概念和方法后[1],对混沌同步的研究成为非线性科学中的热门课题。近年来,人们提出了基于不同角度的各种混沌同步的方法[2],如OGY法、驱动-响应同步法、自适应控制法、主-被动同步法、变量反馈法等。在研究部分线性混沌系统中,Mainieri和Rehacek提出了一种新的投影同步的方法[3],随后,投影同步的研究受到广大学者的重视[4-8]。
本文以一类金融混沌系统为例,研究一个驱动系统对应多个响应系统的广义投影同步方法。
1 问题描述与系统模型
经济学中的混沌现象自1985年首次被发现以来,对西方主流经济学派产生了巨大的冲击,因为经济系统中出现混沌现象意味着宏观经济运动本身具有内在的不稳定性。文献[9]建立了一个由生产子块、货币、证券子块和劳动力子块所组成的金融混沌系统,其数学模型为
(1)
式中x表示利率,y表示投资需求,z表示价格指数,a≥0为储蓄量,b≥0为投资成本,c≥0为商品需求弹性。经过线性变换x1=x,x2=y-1/b,x3=z,系统(1)可以化成
(2)
系统(1)和(2)是拓扑等价的。当a<0.000 01时,产生通货膨胀,混沌现象发生[10]。孙梅、田立新以江苏能源需求与西部能源供给、江苏能源进口量之间相互支持相互制约的复杂关系为背景,建立了一个能源需求-供给的非线性动力学模型(以下简称能源系统),它有着不同于Lorenz系统、Rossler系统等已熟知的混沌系统的复杂的吸引子[11]。其动力学系统方程为:
(3)
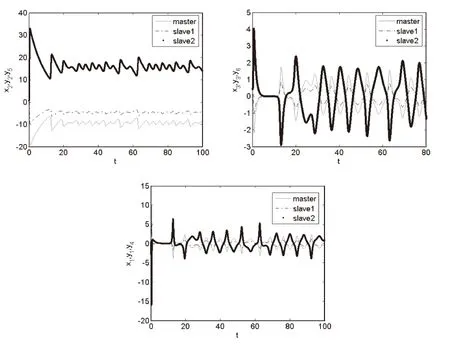
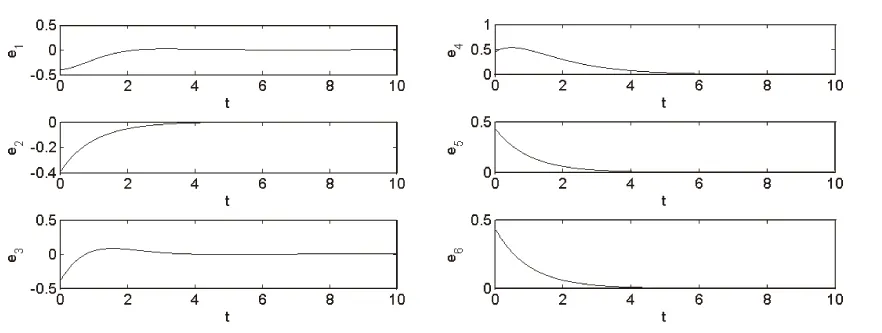
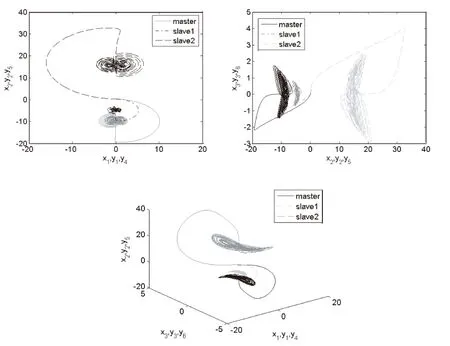
式中ai,bi,ci,M,N均大于零,为常数,N 根据主动控制的思想构造非线性反馈控制器,实现一个驱动系统和两个响应系统的同结构同步。以系统(2)为驱动系统,其同结构的受控系统分别为: (4) (5) 式中,ui(i=1,…,6)是要设计的同步控制器。定义误差信号如下:ei=xi-αyi(i=1,2,3),ei=xi-βyi(i=4,5,6),常数α,β为比例因子。由式(2)分别减去式(4)和式(5),可得同步误差系统为: (6) (7) 根据主动控制的思想,选择控制函数分别为如下: (8) (9) 其中vi(i=1,…,6)分别是关于误差变量ei(i=1,…,6)函数的控制输入信号,只要选择合适的控制输入vi(i=1,…,6)使得误差系统(6)和(7)的所有特征根都有负实部,误差系统最终都是收敛的。为简单起见,选择vi(i=1,…,6)如下: (10) (11) 取步长为0.001,系统(2)的参数a=0.000 01,b=0.1,c=1,驱动系统的初值为(0.1,0.3,0.3),两个响应系统的初值分别为(0.5,0.2,0.5)和(0.1,0.2,0.6),比例因子α=0.5,β=-2进行数值仿真,如图1。其中图1(a)为驱动系统与两个响应系统对应状态输出的变化示意图,图1(b)为同步误差信号的曲线,图1(c)为混沌系统广义投影同步的混沌吸引子。可见,通过主动控制法设计的非线性控制器,能够快速地实现三个相同的金融混沌系统的广义投影同步。 (a)驱动系统和两个响应系统对应状态输出变化 (b)同步误差信号曲线变化 (c)广义投影同步三个相同的混沌吸引子图1 比例因子α=0.5,β=-2的仿真结果 当混沌系统的同步用于安全通信时,驱动系统与响应系统的结构有可能不同,因而考虑异结构的同步更具有实际意义。根据主动控制的思想,设计合适的非线性控制器,实现三个结构完全不相同的混沌系统之间的驱动-响应-响应的广义投影同步。 以系统(2)为驱动系统,系统(12)(为方便起见,将系统(3)写成系统(12)的形式)和Rollser系统(13)为其异结构的受控的响应系统。 (12) (13) 同样,ui(i=1,…,6)是要设计的同步控制器。定义误差信号如下:ei=xi-αyi(i=1,2,3),ei=xi-βyi(i=4,5,6),常数α,β为比例因子。同步误差系统分别为: (14) (15) (16) (17) 其中vi(i=1,…,6)分别是关于误差变量ei(i=1,…,6)函数的控制输入信号,选择vi(i=1,…,6)如下: (18) (19) 则误差系统(14)和(15)的特征值为-1,-1,-c,-1,-1和-c,当t→∞时,ei(i=1,…,6)均收敛于零,称三个异结构的混沌系统获得任意比例的广义投影同步。图2(a),2(b),2(c)为多系统广义投影同步比例因子α=2,β=-0.6,驱动系统的初值为(0.2,0.2,0.2),两个响应系统的初值分别为(0.3,0.3,0.3)和(0.4,0.4,0.4)的仿真结果。 (a)驱动系统和两个响应系统对应状态输出变化 (b)误差曲线变化 (c)广义投影同步三个相同的混沌吸引子图2 比例因子α=2,β=-0.6的仿真结果 由图1和图2可知:当比例因子的绝对值大于1时,响应系统的振幅与驱动系统的振幅相比缩小了;当比例因子的绝对值小于1时,响应系统的振幅与驱动系统的振幅相比放大了。通过改变比例因子α,β可以获得任意比例于原驱动系统的输出混沌信号,实现一个驱动系统和两个响应系统的广义投影同步,这种性质在利用混沌系统进行数字通信保密方面也有广泛的应用前景。 本文利用广义同步的原理,以一类金融混沌系统为例,提出了一个驱动系统对应多个响应系统的广义投影同步方法,成功实现了驱动-响应-响应系统之间的同结构广义投影同步,以及该混沌系统与能源系统、Rossler混沌系统之间的异结构广义投影同步,理论和数值仿真证明了该方法的可行性与有效性。这种方法不仅可以用于其他混沌及超混沌系统的广义投影同步,而且可以推广到一个驱动系统对应三个或更多个响应系统中。 [1] Ott E, Grebogi C ,Yorke J A. Contolling chaos[J]. Phys Rev Lett,1990,64(11):1196-1199. [2] 王瑞光,于熙龄,陈式刚.混沌的控制、同步与利用[M].北京:国防工业出版社,2001:24. [3] Mainieri R, Rehacek J. Projective synchronization in three-Dimensional chaotic systems[J]. Phys Rev Lett,1999,82(15):3042-3045. [4] Peng G Y, Jiang Y L. Generalized projective synchronization of a class of fractional-order chaotic systems via a scalar transmitted signal[J]. Physics Letters A,2008,372(22):3963-3970. [5] 王宇野,许红珍.异结构不确定混沌系统的广义投影同步[J].系统工程与电子技术,2010,32(2):355-358. [6] 谢勇,姚洪兴,张芳.时滞驱动-响应网络系统的函数投影同步[J].复杂系统与复杂性科学,2012,9(4):50-54. [7] 王春华,胡燕,余飞,等.一类混沌系统同步时间可控的自适应投影同步[J].物理学报,2013,62(11):1-7. [8] 安小宇,刘金桂.时滞不确定混沌系统的投影同步控制[J].计算机仿真,2014,31(6):377-380. [9] 黄登仕,李后强.非线性经济学的理论和方法[M].成都:四川大学出版社,1993:55-60. [10] Cai G L, Huang J J. A new finance chaotic attractor[J]. International Journal of Nonlinear Science,2007,3(3):213-220. [11] Sun M, Tian L X, Fu Y. An energy resources demand-supply system and its dynmical analysis[J]. Chaos, Solitons & Fractals,2007,32(1):168-180. (责任编校:夏玉玲) Generalized Projective Synchronization for a Financial Chaotic System LI Zhen (Department of Fundamental Science Teaching, Tangshan College, Tangshan 063000, China) The author of this paper, with a financial chaotic system as an example, proposes a method of generalized projective synchronization with one drive system corresponding to several response systems, achieving a generalized projective synchronization between the drive system and several response systems with the same structures, as well as a generalized projective synchronization between three different types of chaotic systems with different structures. Output chaotic signals in any proportion to the original drive system can be achieved by changing the scale factors of generalized projective synchronization and the numerical simulations demonstrate the effectiveness of this method. financial chaotic system; generalized projective synchronization; scaling factor O231;F830 A 1672-349X(2015)06-0014-03 10.16160/j.cnki.tsxyxb.2015.06.0062 三个同结构混沌系统的广义投影同步


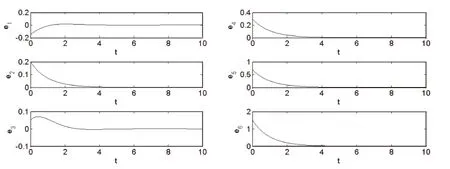
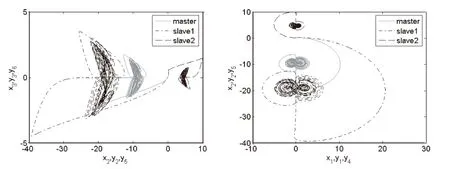
3 三个异结构混沌系统的广义投影同步
4 结论
