Cayley树指标集马氏链的射线常返性

范振耀

(唐山学院 基础教学部，河北 唐山 063000)

Cayley树指标集马氏链的射线常返性

范振耀

(唐山学院 基础教学部，河北 唐山 063000)

给出了Cayley树边界∂TC，2的集合形式，研究在不限定根顶点O的条件下，Cayley树指标集马氏链的射线常返性，得出了Cayley树指标集马氏链或者强常返，或者非常返的结论。

Cayley树；树指标集马氏链；射线常返性

0 引言

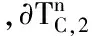
树指标集随机过程是近年发展起来的概率论的一个新的研究方向。Spitzer首先研究了Markov随机场[1]，Berger和叶中行研究了齐次树图上平稳随机场熵率的存在性[2]，杨卫国利用分析方法研究了树指标集马氏链一般的强大数定律，给出了齐次树指标集马氏链的若干极限性质[3]，党慧、杨卫国研究了二叉树上分支马氏链定义的等价形式，并指出，在二叉树情况下，树指标集马氏链是特殊的分支马氏链[4]。树指标集马氏链的概念是Benjamin.I和Peres首先提出来的，其本质是Markov随机场，他们研究了树指标集马氏链常返和射线常返的性质，是假定根顶点O在确定的条件(T0≡x0，x0∈G，G∈N)下讨论的，并且文章提出了若干问题，其中一个问题是树指标马氏链的常返性是否依赖于根顶点x0[5]。范振耀、金少华、边静指出在不限定根顶点O的条件下，有限状态集合树指标集马氏链或者非常返，或者强常返，并给出了在有限状态空间下树指标集马氏链的充分条件[6]。本文将在不限定根顶点O条件下，论证Cayley树指标集马氏链或者强射线常返性，或者非射线常返性。

1 主要结论

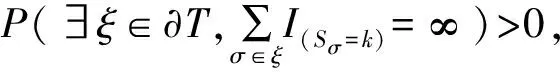
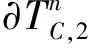
对于Cayley树TC，2第n层共有2n个顶点(n≥0)，设σn为其中任意一个，记作A={σn}。

Step1：若S(σn-1)=σn，则A={σn-1，σn}；

Step2：若S(σi)=σj，则A={σn，σn-1，…，σj，σi}；

Step3：若σi≠0，重复Step2，若σi=0，则A={σn，σn-1，…，σ1，σ0}，其中σ0为根顶点，σi为第i层上的顶点。

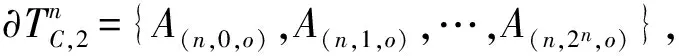
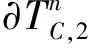
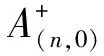
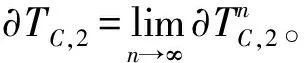
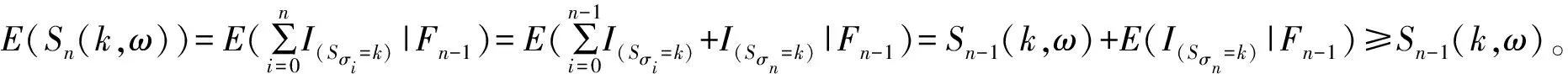
所以{Sn(k，ω)，Fn，n≥1}为一个下鞅。

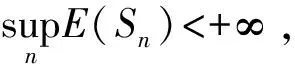
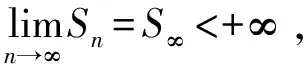
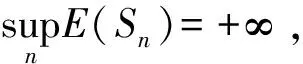
由定理可知，在不限定初始状态下，Cayley树指标集马氏链或者非常返，或者强常返。即我们可以按照常返性将可列状态G分为两个集合G1，G2，当初始状态选G1中元素时，Cayley树指标集马氏链是强常返的，当初始状态选G2时，Cayley树指标集马氏链是非常返的。

[1] Spitzer F. Markov random fields on an infinite tree[J]. Ann Probab，1975(3)：387-398.

[2] Berger T，Ye Z. Entropic aspects of random fields on trees[J]. IEEE Trans inform Theory，1990，36(5)：1006-1018.

[3] Yang Weiguo. Some limit properties for Markov chains indexed by a homogeneous tree[J]. Statistics & Probability Letters，2003，65(3)：241-250.

[4] 党慧，杨卫国.二叉树上分支马氏链的等价性质[J].应用概率统计，2014，30(5)：491-496.

[5] Benjamini I， Peres Y. Markov chains indexed by trees[J].Annals of Probability，1994，22(1)：219-243.

[6] 范振耀，金少华，边静.树指标集马氏链的常返性[J].数学的实践与认识，2009，39(18)：221-223.

(责任编校：夏玉玲)

On the Ray Recurrence of the Markov Chains of the Cayley Tree Index Set

FAN Zhen-yao

(Department of Fundamental Science Teaching， Tangshan College， Tangshan 063000， China)

The author of this paper obtains the set of the Cayley tree boundary of ∂TC，2，studies the ray recurrence of the Markov chains of Cayley tree index set under the condition of unlimited root vertex， and concludes that the Markov chains of Cayley tree index show either strong recurrence or nonrecurrence.

Cayley tree；Markov chains of tree index set； ray recurrence

O211.62

A

1672-349X(2015)06-0009-02

10.16160/j.cnki.tsxyxb.2015.06.004