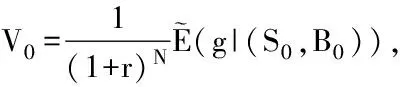离散鞅论在多期期权定价中的推广

周一美

(渤海大学 数理学院，辽宁 锦州 121013)

离散鞅论在多期期权定价中的推广

周一美

(渤海大学 数理学院，辽宁 锦州 121013)

研究了离散鞅论在多期期权定价下的推广。通过假设前提，确定了多期期权模型的结构，分析其欧式期权的性质，并运用反证法和单期模型的相关理论得出了多期期权下的关系式。

离散鞅论；期权定价；多期期权定价；欧式期权

近年来，期权模型的应用研究受到国内广大学者的关注，杨建奇、肖庆宪对期权定价的方法和模型进行了综合描述[1]，付蔷对鞅理论及其在某些金融模型中的应用进行了相关研究[2]。在国外，Black F， Scholes M等将B-S模型作为期权定价中的经典方法，对其假设的局限性和模型本身参数估计中所存在的偏差做出了反思[3-4]。金融学家们在此基础上建立了资产定价基本定理[5]。本文将对单期期权模型进行推广，以得到离散鞅论在多期模型下的关系式。

1 期权定价的多期模型

N期(多期)模型的假设前提：金融市场是无套利市场，N期股票收益是独立分布的。选择X=(0，1)N作为N期模型的适应样本空间，样本点为x=(x1，x2，x3，…，xN)，x∈X。n≤N时，Sn是期权到期时刻为n时的股票价格，并由x*=(x1，x2，x3，…，xN)决定。

显然Sn(x)≡Sn(x*)，则股票价格变化为：

a，b，p的定义同单期模型，且满足0<1+r

定义空间X上的概率测度P为：

设不同的期权到期时刻为0，1，2，…，N，令V1，V2，V3，…，VN为股票价格是S1，S2，S3，…，SN，且期权的执行价格为K时的欧式期权价格，则有

2 将单期模型中的方法引入到多期模型中

设一个N期模型的资产组合系数为{(αn，βn，γn)，n=0，1，2，…，N}，αn，βn，γn是定义在X={0，1}N上的随机变量，且x=(x1，x2，x3，…，xN)。

其中：

定理1 在期权到期时刻为1，2，3，…，N时，欧式期权价值分别为V1，V2，V3，…，VN，则有递推关系式：

(1)

证明 与单期模型中的证明方法相同，首先用反证法证明，假设ε=Vn-1-(βn-1Sn-1+γn-1Bn-1)>0。

(2)

在t=n时刻的财富过程是：

(3)

将Vn=g代入式(3)中得：

由于对所有的x∈X，Bn，Bn-1均为正，故Wn(x)>0，与无套利前提矛盾。

故Vn-1-(βn-1Sn-1+γn-1Bn-1)=0。

将βn-1，γn-1代入后得到期权的价格递推关系式：

(4)

以此类推分别求出Vi-3，Vi-4，…，V0。

故期权的初始价格满足：

[1] 杨建奇，肖庆宪.期权定价的方法和模型综述[J].商业时代，2008(16)：65-81.

[2] 付蔷.鞅理论及其在某些金融模型中的应用[D].哈尔滨：哈尔滨工业大学，2012.

[3] Black F， Scholes M. The pricing of options and corporate liabilities[J]. Journal of Political Economy，1973，81：637-659.

[4] Harrison J M， Kreps D M. Martingales and arbitrage in multiperiod securities markets[J]. Journal of Economic Theory，1979，20：381-408.

[5] 邵宇.微观金融学及其数学基础[M].北京：清华大学出版社有限公司，2003：240-243.

(责任编校：夏玉玲)

Application of Discrete-time Martingale to Multi-period Option Pricing

ZHOU Yi-mei

(College of Mathematics and Physics， Bohai University， Jinzhou 121013， China)

In this paper， the authors study the promotion of discrete-time martingale theory in multi-period option pricing， determine the structure of the multi-stage option model by assuming the premise， analyze the nature of the European option， and obtain the relationship under multi-period option with reductio ad absurdum and the single-phase model.Key Words： discrete-time martingale； option pricing； multi-period option pricing； European option

O211.9

A

1672-349X(2015)06-0007-02

10.16160/j.cnki.tsxyxb.2015.06.003