分层协同进化的果蝇优化算法

乐 天，陆慧娟，崔振东，张 威

（1.浙江海洋学院数理与信息学院，浙江舟山 316022；2.浙江省海洋大数据挖掘与应用重点实验室，浙江舟山 316022；3.中国计量学院信息工程学院，浙江杭州 310018）

分层协同进化的果蝇优化算法

乐 天1，2，陆慧娟3，崔振东1，2，张 威1，2

（1.浙江海洋学院数理与信息学院，浙江舟山 316022；2.浙江省海洋大数据挖掘与应用重点实验室，浙江舟山 316022；3.中国计量学院信息工程学院，浙江杭州 310018）

果蝇优化算法（FOA）是较新的群智能算法，其应用领域越来越广泛。但该算法在求解问题时存在早熟收敛，收敛速度慢和收敛精度低的缺点，为改善算法性能本文提出了分层协调进化的果蝇优化算法(HCFOA)。根据味道浓度值将果蝇种群分层，并结合果蝇个体的进化信息及精英个体对种群位置的影响，进行分层协同进化。HCFOA和FOA分别求解4个测试函数，仿真结果表明，HCFOA算法有效改善了局部搜索能力，提高了收敛精度。

果蝇优化算法；分层协同进化；收敛精度

群智能算法是模拟生物为求生存所具有的本能和方法发展而来的算法，包括遗传算法，蚁群算法，粒子群算法，免疫算法，鱼群算法，萤火虫算法，果蝇优化算法等。其中的果蝇优化算法是一种模拟果蝇觅食行为的全新的全局优化算法，在2011年6月由潘文超提出。FOA已成功应用于求取函数极值[1]，自动化仓库拣选作业调度问题[2]和船舶操纵响应模型的辨识[3]与语音信号盲分离[4]等。但因FOA发展时间较短，目前还处于研究的初级阶段，迫切需要更多的研究者展开关于FOA的相关研究。

相比其他群智能算法，FOA算法描述简单，容易实现，需调参数较少、有较强的全局搜索能力和鲁棒性，但同时与其他群智能算法一样标准果蝇优化算法存在易陷入局部解，收敛精度低，收敛速度慢等缺点，许多学者已进行了相关的研究。文献[5]提出不仅要向优秀果蝇学习，同时要向最差果蝇学习的改进策略。文献[6]在果蝇算法中融入Logistic映射改进初值选取来改善算法搜索性能。文献[7]利用元胞自动机有效克服果蝇优化算法陷入局部解的缺点。

针对果蝇优化算法存在早熟收敛，不易跳出局部最优，且收敛精度低和收敛速度慢的缺点，本文受种群存在阶层现象，且不同阶层间可以协同发展的启发，提出分层协同进化的果蝇优化算法。将果蝇种群按其味道浓度值分成两层，形成高味道浓度值种群和低味道浓度值种群。高味道浓度值种群充分考虑个体的进化信息，加强其局部勘探能力；低味道浓度值种群利用双精英个体对种群位置的影响，提高算法的收敛速度和精度。将FOA和HCFOA应用于4个基准测试函数进行比较，仿真结果说明本文所提出的HCFOA有效改善了算法性能。

1 标准果蝇优化算法

果蝇的嗅觉和视觉器官功能强大，利用嗅觉器官能搜索到40 km以外的食物源，利用视觉器官可以找到食物以及果蝇群聚集的位置，并飞向该位置。果蝇优化算法是依照果蝇的嗅觉和视觉搜寻食物的特性推演出的一种全局优化算法[1]。该算法通过一定量的代表问题解的果蝇个体组成果蝇种群，并依据最优果蝇个体的位置，使种群中的其它个体按随机设定的方向和距离汇集到该位置，如此一代代迭代，搜寻到食物。算法流程如图1所示，具体步骤如下：

step1：给定种群规模POPSIZE和最大迭代次数MAXGEN，根据搜索范围随机给出果蝇种群初始位置：X’，Y’；

step2：模拟果蝇个体利用嗅觉搜寻食物：以种群所在位置为中心，以随机给定的飞行方向和距离VALUE值确定个体搜索食物新的位置：

step3：为计算果蝇个体嗅到的食物味道浓度，因不知食物位置，故需先计算个体和原点之间的距离DISi，再设置味道浓度判定值，距离越短，味道浓度判定值越大，因此将距离倒数作为味道浓度判定值SSi:

step4：求取果蝇个体所在位置的味道浓度值SEMLLi（味道浓度判定值SSi代入适应度函数）:

step5：找到最优个体BEST，味道浓度最大的果蝇（当前代最优个体）将是同伴聚集的位置；

step6：模拟果蝇种群利用视觉飞向聚集位置，即保存个体BEST的味道浓度值及其坐标：

step7：在未迭代到MAXGEN时，循环运行step（2）～step（5），若当前代最优个体优于前一代最优个体则执行step（6）。

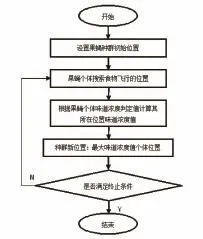
图1 FOA算法流程图Fig.1 FOA flow chart

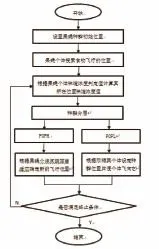
图2 HCFOA算法流程图Fig.2 HCFOA flow chart

2 分层协同进化的果蝇优化算法

理论上，FOA中的果蝇种群凭借果蝇的视觉和嗅觉能够搜索到问题的全局最优解，但整个算法中有以下两个步骤值得关注：一是在步骤（6）中，因果蝇种群集体飞向味道浓度值最大的个体，若当前最优果蝇个体指引出错，算法极容易陷入局部最优；并且只依靠最优果蝇个体而完全舍弃个体本身的进化信息，造成对潜在优秀个体的勘探不足，算法不易跳出局部最优。二是算法步骤（2）中VALUE取值的随机性未能体现果蝇个体存在的差异性。VALUE取值过大，果蝇个体飞出最优解的范围而使算法陷入局部解；VALUE取值过小，果蝇个体虽在最优解的范围，但算法收敛速度缓慢。

HCFOA算法充分考虑个体进化信息及其差异性，以克服算法局部搜索能力不足，加快收敛速度，提高收敛精度。该算法在标准果蝇优化算法的基础上，对种群进行了分层，不同层按不同的策略进行寻优，利用果蝇个体信息，增强果蝇个体勘探全局最优解的方向性和能力性。

定义1（种群分层）：设果蝇种群表示为P(t)={at1,at2,...,atn},其中t为迭代数，n为种群规模，s(x)为果蝇个体的味道浓度值。令做集合则集合SMELL_Lt= P(t)-SMELL-Ht。

按定义1进行果蝇种群分层，分别形成高味道浓度值种群SMELL_H和低味道浓度值种群SEMLL_L。针对SMELL_H种群，因个体具有良好的进化信息，在充分利用果蝇自身所在的位置信息的基础上，对设置果蝇搜索食物的方向与距离的VALUE值进行了自适应的调整，自适应调整如下：

其中DISiH表示果蝇个体离最高味道浓度值果蝇个体的距离，DISavg表示SMELL_H种群的平均距离，DISmax表示SMELL_H种群中距离最高味道浓度值果蝇个体的最大距离。DISavg反应SMELL_H种群的密集程度，其值越小表示果蝇种群越集中在最高味道浓度值个体周围。当DISiH＞=DISavg时，对VALUE以一定的比例进行调整，DISiH愈大，调整比例愈大，确保果蝇个体对最高味道浓度值果蝇个体周边区域的勘探能力，使其能更有效地跳出局部解；DISiH＜DISavg时，按FOA算法进行全局搜索。

针对SEMLL_L种群，受到生物进化过程中不同种群其最优个体对种群的推动作用和层间个体相互协作的启发，新的飞行位置不仅受SMELL_H种群中最高浓度值个体的影响，同时也受到SEMLL_L种群中最高浓度值个体的控制，具体如下：

采用两层双精英个体协同来确定种群将要飞向的位置，引导SEMLL_L种群朝最优解方向飞行，确保其更好的全局搜索方向，提高全局搜索能力。

合并由SEMLL_H种群和SEMLL_L种群产生的个体作为新的种群，两层种群协同进化，不仅有利于算法跳出局部解，同时也进一步提高其收敛速度和求解问题的精度。

遵循标准果蝇优化算法的算法框架，本文提出的HCFOA算法流程如图2所示，具体步骤如下：

step1：给定种群规模POPSIZE和最大进化代数MAXGEN，随机给出果蝇种群初始位置：X’，Y’；并设置果蝇个体飞行的位置Xi和Yi；

step2：执行FOA中的步骤（3）～（4）；

step3：根据定义1将果蝇种群分为两层SMELL_H和SEMLL_L；

step4：分别记录并保存SMELL_H和SEMLL_L中最优果蝇个体位置及浓度值：

step5：对于SMELL_H种群，计算果蝇个体i与SMELLBEST_H之间的距离转

step6；

step6：计算果蝇个体的新位置:

step7：对于SMELL_H种群，按式（10）和（11）得到XH’’和YH’’，个体飞行位置如下：

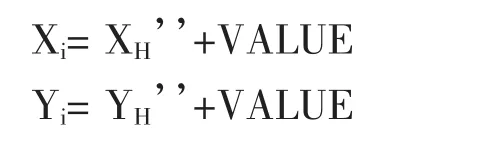
step8：循环迭代step2～step7，直到满足结束条件（最大进化代数，进化精度等）。

3 实验

3.1 实验内容

为验证本文提出的算法的有效性，将其应用于4个常用的性能测试函数，并与FOA仿真结果进行对比。函数信息见表1。测试函数的优化难度随着其维数的增大，搜索范围的扩大和目标精度的提高而加大。本文选用的维数和搜索范围都是比较严苛的。实验在win 7操作系统和vc++6.0，机器主频为3.4GHz，内存为4G环境下仿真实现。

3.2 实验结果分析

实验具体参数设置为：popsize=15，maxgen=2000，X’，Y’为表1中所列搜索范围，VALUE取值区间[-1，1]。由于算法中的果蝇种群初始位置和搜索范围取值具有一定的随机性，HCFOA和FOA分别运行20次，取每代中最优果蝇个体的味道浓度值的算术平均值。

图1是HCFOA和FOA求解函数最优值的对数值进化曲线，本文对最大味道浓度值进行了取对数处理，主要是为了方便查看曲线，同时考虑若真数为0，对数取值直接设置为-40。从图1的进化曲线可以看出，不管是对于单峰值函数（f1和f3）还是对于多峰值函数（f2和f4），HCFOA的搜索能力，收敛速度和精度均明显优于FOA。

表1 优化函数Tab.1 Optimized function

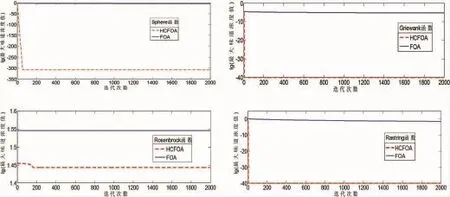
图3 f1～f4最大味道浓度值进化曲线Fig.3 Maximum fitness volutionary curves of f1～f4

表2是HCFOA与参考文献算法的性能比较。参考文献算法对应的搜索范围，种群规模和最大进化的取值见表3。相对于参考文献中的算法，HCFOA在较大的搜索范围和较小的种群规模和迭代次数取值下，除f3在GAFSA求解中优化均值稍优于HCFOA，其他均比参考文献具有更优的收敛精度。f2，f4表现尤其突出，能够很好的跳出局部最优，搜索到全局最优解。

表2 优化均值比较Tab.2 Comparison of optimization mean

表3 各函数相关数据设置Tab.3 Function parameters setting

4 结束语

本文分析了标准果蝇优化算法在优化过程中因只考虑飞向最优果蝇个体和VALUE取值的随机性，引起算法陷入局部最优，收敛速度慢和收敛精度低等问题，提出一种分层协同进化的果蝇优化算法。并用HCFOA算法求解4个性能测试函数，和FOA求解结果对比表明，本文提出的HCFOA算法具有更好的勘探最优解的能力，其收敛速度和收敛精度都有明显地提高。

[1]PAN Wen-Tsao.A New Evolutionary Computation Approach:Fruit Fly Optimization Algorithm[C]//Proc.of the 11th Con-ference on Digital Technology and Innovation Manage-ment.Taipei,China:[s.n.],2011.

[2]刘志雄,王雅芬,张 煜.多种群果蝇优化算法求解自动化仓库拣选作业调度问题[J].武汉理工大学学报,2014,36(3):71-77.

[3]韩俊英,刘成忠.基于果蝇优化算法的船舶操纵响应模型的辨识[J].大连海事大学学报,2012,38(3):1-4.

[4]肖正安.改进FOA算法在语音信号盲分离中的应用[J].计算机工程与应用,2013,49(16):201-204.

[5]韩俊英,刘成忠.反向认知的高效果蝇优化算法[J].计算机工程,2013,39(11):223-225.

[6]程 慧,刘成忠.基于混沌映射的混合果蝇优化算法[J].计算机工程,2013,39(5):218-221.

[7]贺智明,宋建国,梅宏标.结合元胞自动机的果蝇优化算法[J].计算机应用,2014,34(8):2 295-2 298.

[8]王 凌.智能优化算法及其应用［M］.北京:清华大学出版社，2001:148－149.

[9]林 川，冯全源.一种新的自适应粒子群优化算法[J].计算机工程，2008，34(7):181－183.

[10]王联国，洪 毅，施秋红.全局版人工鱼群算法[J].系统仿真学报，2009，21(23):7483－7486.

Hierarchical Coevolutionary Fruit Fly Optimization Algorithm

LE Tian1,2,LU Hui-juan3,CUI Zhen-dong1,2,et al
(1.School of Mathematics,Physics and Information Science,Zhejiang Ocean University,Zhoushan 316022; 2.Key Laboratory of Oceanographic Big Data Mining&Application of Zhejiang Province,Zhoushan 316022; 3.College of Information Engineering,China Jiliang University,Hangzhou 310018,China)

Fruit Fly Optimization Algorithm(FOA)is a relatively new Swarm intelligence algorithm,its application field is more and more widely.In solving the problem using this algorithm,low convergence precision and easily relapsing into local optimum,there are the faults of Premature convergence,slow convergence speed and low convergence precision.Hierarchical Coevolutionary Fruit Fly Optimization Algorithm (HCFOA)is proposed in order to improve the algorithm performance in this paper.Fruit fly population is layered according to smell,and coevolutioned with the evolution information and the effects of elite individual on population location.The simulation results of four test functions show that HCFOA has the advantages of better local searching ability,and more precise convergence than FOA.

fruit fly optimization algorithm(FOA);fierarchical coevolutionary;convergence precision

TP18

A

1008－830X(2015)05－0491－06

2015-02-10

浙江省科技厅公益技术研究社会发展项目（2015C33082）

乐天（1978-），女，浙江舟山人，讲师，硕士，研究方向：智能计算.E-mail:103405954@qq.com