Hilbert空间中逆强单调映像的迭代算法的收敛性

张建秋，郝 彦，郝 妍

（浙江海洋学院数理与信息学院，浙江省海洋大数据挖掘与应用重点实验室，浙江舟山 316022）

Hilbert空间中逆强单调映像的迭代算法的收敛性

张建秋，郝 彦，郝 妍

（浙江海洋学院数理与信息学院，浙江省海洋大数据挖掘与应用重点实验室，浙江舟山 316022）

在实Hilbert空间框架下研究逆强单调映像的变分不等式的解的迭代算法，并且证明了该迭代序列是强收敛的。该文结果是一些学者早期与最近的相应结果的改进与推广。

变分不等式；逆强单调映像；迭代算法

1 引言和预备知识

设H是实Hilbert空间,其范数和内积分别为‖·‖和〈·，·〉,C是H的一个非空闭凸子集.A∶C→H是非线性映像.

定义1.1[1]若对于每一个x,y∈C有〈Ax-Ay，x-y〉≥0,则称A是单调的.

定义1.2[1]若存在常数α＞0,满足〈Ax-Ay，x-y〉≥α‖x-y‖,x,y∈C,则称A是强单调的,也称之为α-强单调.

定义1.3[1]若存在常数满足则称A是逆强单调的,也称之为α-逆强单调.

在Hilbert空间中我们用xn→x表示序列{xn}弱收敛于x,用xn→x表示序列{xn}强收敛于x,对于任意x∈H,在C上必存在唯一一点,记为PC,满足‖x-PCx‖≤‖x-y‖对于所有y∈C.是度量投影,显然PC∶H→C是非扩张映像,并且PC满足

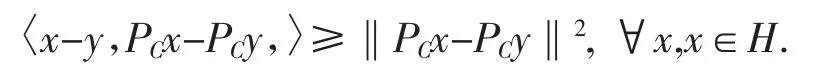
变分不等式问题可以理解为

变分不等式的求解是最优化方法的一个重要分支.人们对变分不等式的兴趣始于对力学问题的研究.到了上个世纪60年代,变分不等式才作为一门数学学科被人们广泛研究.

最近,许多专家学者对变分不等式问题的解集和Hilbert空间中的逆强单调映像不动点解集的公共元进行了广泛研究.

为了解决逆强单调映像不动点的解,Iiduka[2]构造了一个迭代算法,并证明了该迭代序列是弱收敛的.

本文受Iiduka等文献的启发,研究逆强单调映像不动点的强收敛性.

为了证明本文的主要结论,我们需要以下引理.

引理1.1（Xu[3]）假定{αn}是一个非负实数序列,满足

{γn}是(0,1)中的序列,{δn}是一个数列,满足

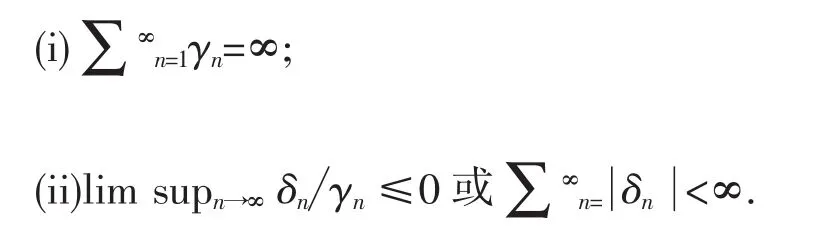
则limn→∞αn=0.

引理1.2(Aoyama,Hiduka and Takahashi[4])设C是Hilbert空间的H一个非空闭凸子集.PC∶H→C是一个度量投影,A∶C→H是一非线性算子.则对于所有的λ＞0,

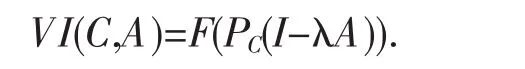
2 主要结论

定理2.1设H是实Hilbert空间,C是H的一个非空凸子集.A∶C→H是α-逆强单调映像且VI(C,A)≠Ø.设x1=x∈C,{xn}由下式生成

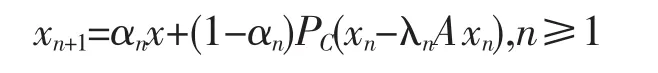
其中{αn}是(0,1)中的一个序列,{λn}是[0,2α]中的一个序列.如果{λn}满足λn∈[a,b],其中a,b满足0＜a＜b＜2α,且{αn},{λn}满足下列条件

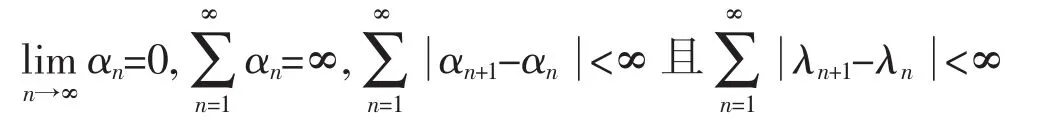
则{xn}强收敛于

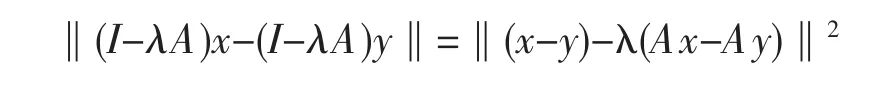
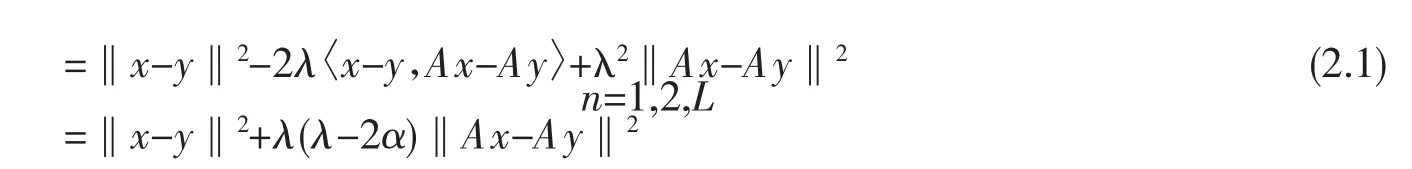
由于λ≤2α，则I-λA是非扩张映像.

设yn=PC(xn-λnAxn),n≥1,u∈VI(C,A).由于I-λnA是非扩张的,且由(1.1)有u=PC(u-λnAu),于是

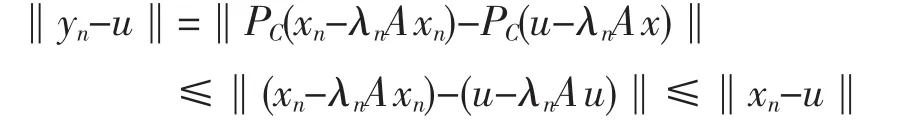
则

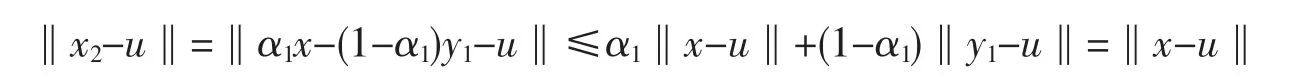
假设对于k∈N,‖xk-u‖≤‖x-u‖成立.可以推证‖xk+1-u‖≤‖x-u‖.因此,序列 {xn}有界,于是{yn},{Axn}也是有界的.由于I-λnA是非扩张的,则

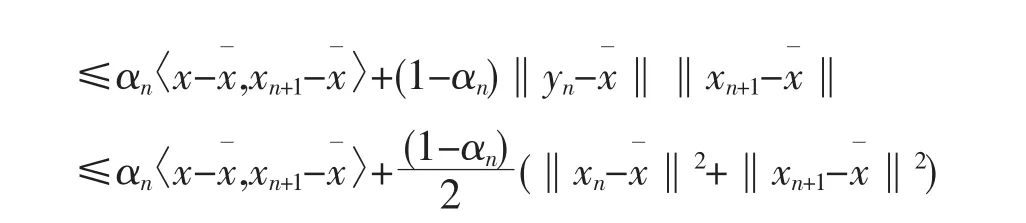
由此可知,

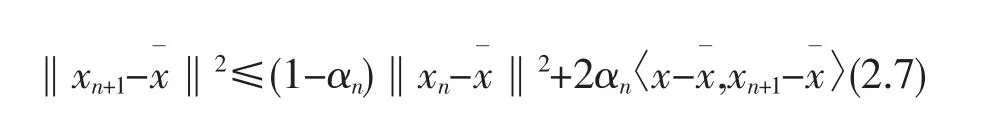
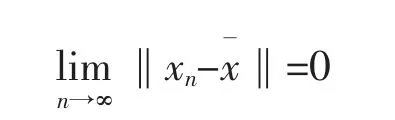
这样就完成了证明.

[1]QIN X L,CHANG S S,CHO Y J.Iterative methods for generalized equilibrium problems and fixed point problems with applications[J].Nonlinear Anal:Real World Applications,2010,11(4):2 963-2 972.

[2]IIDUKA H,TAKAHASHI W,TOYODA M.Approximation of solutions of variational inequalities for monotone mappings[J]. PanAmer Math J,2004,14(2):49-61.

[3]XU H K.Iterative algorithms for nonlinear operators[J].J London Math Soc,2002,66(1):240-256.

[4]AOYAMA K,IIDUKA H,TAKAHASHI W.Weak convergence of an iterative sequence for accretive operators in Banach spaces[J].Fixed Point Theory Appl,2006,Article ID 35390(2006).

Convergence Theorems of An Iterative Algorithm for Inversestrongly Monotone Mappings in Hilbert Spaces

ZHANG Jian-qiu,HAO Yan,HAO Yan
(School of Mathematics,Physics and Information Science,Zhejiang Ocean University,Key Laboratory of Oceanographic Big Data Mining&Application of Zhejiang Province,Zhoushan 316022,China)

The purpose of this paper is to consider an iterative algorithm for finding solutions to a variational inequality for inverse-strongly monotone mappings.Strong convergence theorems are proved.The results improve and extend the corresponding results of many others.

variational inequalities;inverse strongly monotone mappings;iterative algorithm

O177.1

A

1008-830X(2015)05-0486-05

2015-03-10

浙江省自然科学基金项目（Y6110270）

张建秋（1990-），男，江苏淮安人，硕士研究生，研究方向：非线性泛函分析.

郝彦（1965-），女，黑龙江齐齐哈尔人，教授，研究方向：非线性泛函分析.