基于FPGA的巴克码相关器设计与研究

张　鑫，孙海青

(中国船舶重工集团公司第七二四研究所，南京211153)

基于FPGA的巴克码相关器设计与研究

张鑫，孙海青

(中国船舶重工集团公司第七二四研究所，南京211153)

摘要：分析巴克码的设计及其相关的特点与原理，用Verilog语言编写相关器，利用FPGA实现13位巴克码相关器，并对其用Modelsim仿真。仿真证明输出了最大功率主副比，有效抑制了旁瓣，并为雷达工程中巴克码的应用提供更坚实的理论基础。

关键词：雷达；信号处理；FPGA；巴克码；相关器；旁瓣抑制

0引言

雷达系统最基本的任务是完成对目标的检测，从而实现对目标的跟踪和定位。然而，由于雷达微弱目标回波信号总是处在各种各样的噪声环境中，其直接影响系统对目标回波的处理质量，如降低对目标的检测能力，降低目标的跟踪定位精度。相关器根据信号和噪声相关函数的差异进行检波，周期信号的自相关函数仍然是周期的，且随时间衰减得很慢。而噪声由于其随机性，在相关器中随时间衰减的很快，因此相关器可以从信号和噪声的混合波形中检测出目标信号[1]。巴克码由于具有尖锐的自相关函数，从而可以将淹没在噪声下的基于巴克码波形的微弱目标信号有效相关出来，实现对信号与噪声的分离，因此常用于雷达信号波形设计中。

Verilog HDL是一种全方位的硬件描述语言，包括系统行为级、寄存器传输级、逻辑门级等多个设计层次，支持结构、数据流和行为3种描述形式的混合描述[2-3]。将巴克码相关器采用Verilog语言在FPGA中实现，可以借助FPGA的并行性实现信号相关检测的高速实时特性。

1巴克码相关器原理

1.1　m序列

m序列是最长线性移位寄存器序列的简称[4]。它具有优良的自相关函数，易于产生和复制，在扩频通信中得到了广泛的应用。m序列也是研究和构造其他序列的基础。

m序列是由线性反馈移位寄存器产生，如图1所示。图中a0,a1,…，an-1表示移位寄存器的状态，c0，c1，…，cn-1为对应级移位寄存器的反馈系数，ci=0表示该反馈断开，ci=1表示该反馈存在。

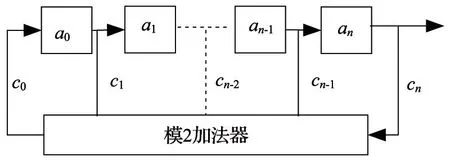
图1　m序列产生原理图

对于反馈移位寄存器产生的序列，取决于反馈系数，其反馈逻辑表示为

F(x)=c0+c1x+c1x2+…+cnxn

(1)

式(1)称为m序列的特征多项式。特征多项式一旦确定，那么其产生的伪随机序列也就确定了。经严格的证明:若反馈移位寄存器的特征多项式为本原多项式，则移位寄存器就能产生m序列，且其周期为N=2n-1，n为寄存器的个数。

在m序列长度为15位时，m序列的功率谱见图1。从图中可以看出m序列的功率谱特点：(1)由于自相关函数的周期性，其功率谱是一个线状谱；(2)谱线包络由m序列码元宽度Tc决定与周期序列无关。

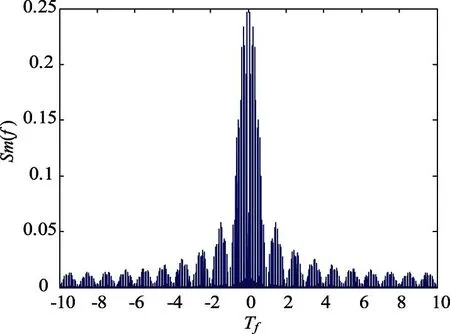
图2　15位m序列的功率谱

m序列功率谱宽度理论值为无穷大，但主要能量集中在第1个零值点之内，其约占总能量的90%。所以，实际上，也经常把f=0~1/Tc这段频率范围称为伪码序列的频带宽度，记作△f。

(2)

m序列具有如下性质:

(1) 平衡性:m序列的一个周期中，“1”的个数与“0”的个数基本相等，确切地说，“1”的个数比“0”的个数多1个。

(2) 游程分布:每个周期内，总共有2n-1个游程，其中长度等于k,1≤k≤n-2的游程占游程总数的1/2。“0”和“1”的游程数目各占一半，长度为n-1的游程只有1个为全“0”游程，长度为n的游程也只有1个为全“l”游程。

(3) 移位可加性:1个m序列同该序列的任意移位(循环移位)序列相加(模2加)，仍是m序列。

1.2　barker序列

barker序列也称为巴克码，也是一种伪随机二维序列，其非周期自相关函数很类似白噪声的自相关函数。二元伪随机序列的非周期自相关函数如下：

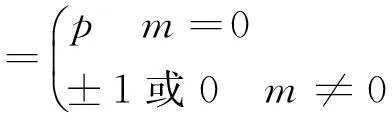
(3)

这个二元伪随机序列就称为巴克序列。这种序列的非周期自相关函数只有4种可能值，最大值为P，最小值为±1或0。但是，巴克码有一个很重要的缺点，就是巴克序列很短，目前只找到9种巴克序列，最长为P=13。13位巴克序列的自相关函数具有类似白噪声自相关函数的特性，如图3所示。

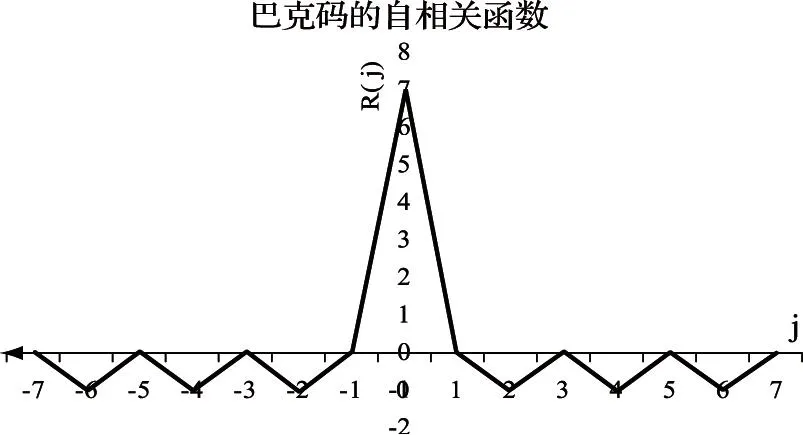
图3　barker码自相关函数图

根据巴克码的频谱和自相关特性，巴克码也是一种性能比较优良的伪随机码。但是，巴克码的本身长度太短，在实际运用中受到了很大的限制。人们找了一种增加巴克码长度的方法，称为组合巴克码。

组合巴克码就是用一个巴克码作为码元(内码)组成另一个新的巴克码(外码)。这个新的巴克码就是组合巴克码。例如，以4为巴克码{+ + - +}作为基本码元，做成一个新的4位巴克码：

其中-Bi(4)为Bi(4)的反码，即-Bi(4)={-,-,+,-}。所以，新的16位巴克码为

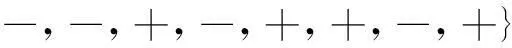
新的16位巴克码自相关函数如图4所示。可以看出，组合巴克码的旁瓣特性既不完全同于内码旁瓣特性，也不完全同于外码特性。组合巴克码主峰附近的最大电平是由外码的码长决定，而远离主峰旁瓣变化规律与内码的自相关函数特性相同。根据计算可以得16位组合巴克码自相关函数主峰近区和远区的最大主旁瓣比电平和15位m序列自相关函数主峰近区和远区的最大主旁瓣比电平。

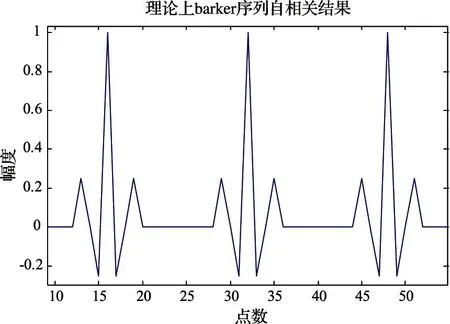
图4　组合巴克码自相关函数

由巴克码的自相关函数图可以看出，组合巴克码的旁瓣性质没有m序列的旁瓣性质好。近、远区的主旁瓣比如表1所示。由表可以看出，虽然同等位数的巴克码主旁瓣比与m序列相近，但组合16位巴克码的近远旁瓣比都小于m序列。这对于伪随机序列的自相关性能会带来很大的影响，降低了其抗干扰性能是重要的影响之一。数字信号处理方案是在频域进行的，但组合巴克码的长度能很方便取到2N位。这样能很方便地通过对雷达的信号与噪声进行FFT变换(先补零)后得到其频谱函数,与传输函数相乘后即为频率响应,再经IFFT变换,求匹配滤波器传输函数来实现输出时域波形。如果需要进一步提高主旁瓣信噪比，则需要对每一码元再进行编码，通过增加延迟加权周期，可进一步降低旁瓣电平。这部分的取舍取决于系统的要求。

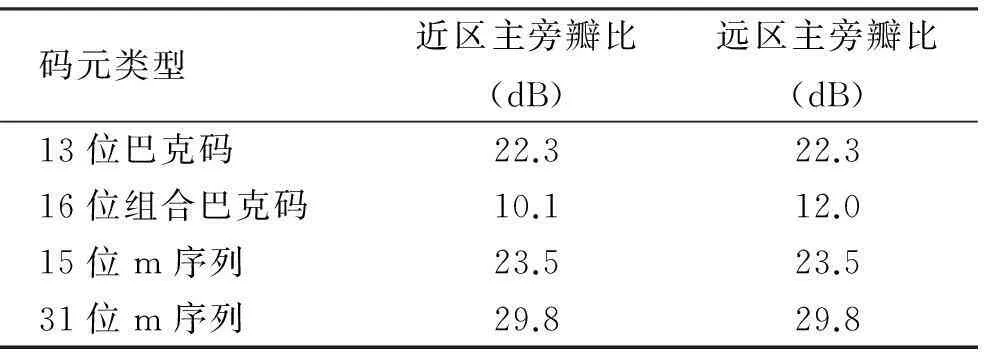
表1　巴克码和m序列近远区主旁瓣比

2Verilog实现仿真与结论

2.1　Barker码的相关器的Verilog实现

通过以上Barker码的理论研究后便开始13位Barker码的设计实践。在创建了barker13_acu2模块后，设计了时钟I_clk,16位数据输入端I_data，以及延迟8位的延时的周期数信号I_delay_num，最后输出20位结果O_result。而Barker码相关器测试向量Testbench的设计，采用了在对相关器初始化并复位后直接输入预先生成的16位定点模拟回波的方法，即直接在每个延迟200ns的时间点上给予I_data确定的定点值，以此来判断输出信号O_result是否符合Barker码的自相关性。

2.2　仿真结果与结论

根据相关器的实现框图，方案为使用负数为取反加一的方法实现与-1的乘法,可以得到13位Verilog语言实现。在整个架构完成后进行了测试向量Testbench 设计。对相关器初始化复位后，输入预先生成的16位定点模拟回波，并得到了Modelsim功能仿真结果。见图5。

在图5中，R_code_shift 代表本地的13位barker码，I_data代表输入的13位barker码，O_result代表输入信号与本地码相关后的输出，R_delay_num代表着距离门数。当其值递减到12时，输入信号的barker码与本地的barker码开始积累，积累13个时钟周期后输出达到最大幅值，实现了Barker码的相关器。将Modelsim功能仿真结果导出，送回matlab进行对比，近远区主旁瓣比均接近于22.3dB,可以看出两仿真结果一致，实现了13位barker相关。

3结束语

基于FPGA的巴克码相关器很好地实现了巴克码脉冲回波信号的相关，有效地实现了噪声环境下微弱目标回波信号的提取，仿真结果也与实际使用情况是相吻合的。后续再通过组合巴克码加权实现高主副比以及长码下多普勒处理等工程方法的解决，可以使巴克码波形在雷达中得到更广泛的应用。

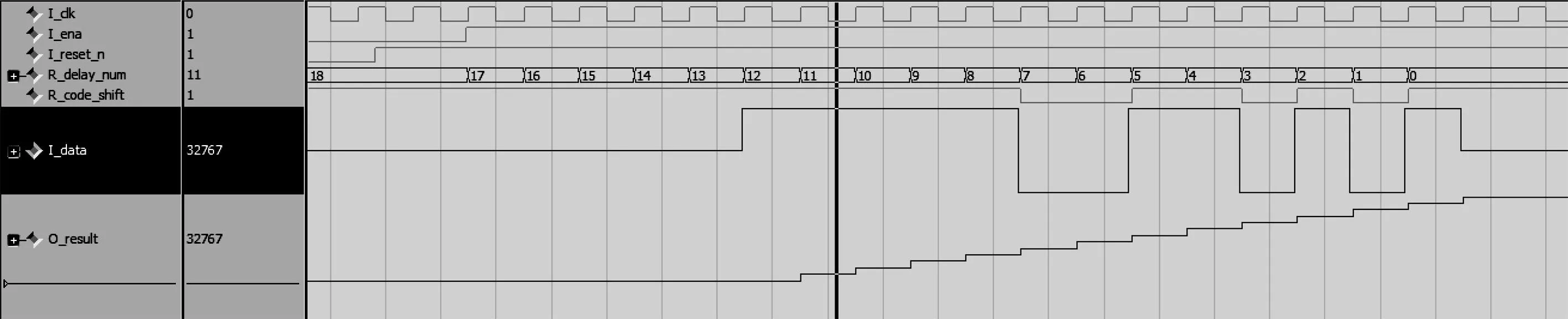
图5Modelsim功能仿真结果

参考文献：

[1]王心水.基于fpga的巴克码发生器与识别器的设计[J].电子技术,2010(2).

[2]龙光利.巴克码识别器的设计与FPGA的实现[J].科技广场,2006(4).

[3]张增良,焦智,周涛.基于CPLD的巴克码信号发生器与译码器[J].华北航天工业学院学报,2005(03).

[4]Jackson W,edBarker R H.Communication Theory[M].New York: Academic Press Inc,1953:273-287.

[5]Cohen M N.现代雷达原理[M].卓荣邦,杨士毅,等译.北京:电子工业出版社,1991:480-517.

Design of a Barker code correlator based on FPGA

ZHANG Xin, SUN Hai-qing

(No.724 Research Institute of CSIC, Nanjing 211153)

Abstract:The Barker code and its characteristics and principle are analyzed. The 13-bit Barker code correlator is designed with Verilog language based on the FPGA, and then simulated via the Modelsim. The simulation results indicate that the maximum master-to-slave power ratio is output and the sidelobe is suppressed effectively, providing a solider theoretical foundation for the application of Barker code in radar engineering.

Keywords:radar; signal processing; FPGA; Barker code; correlator; sidelobe suppression

中图分类号：TN911.7

文献标志码：A

文章编号：1009-0401(2015)04-0039-04

作者简介:张鑫(1981-)，男，工程师，研究方向：雷达总体技术；孙海青(1983-)，男，工程师，研究方向：雷达信号处理。

收稿日期：2015-04-28；修回日期：2015-07-20