服务航天器超近程逼近失控目标的建模与控制

靳永强 张庆展 康志宇 唐平（上海宇航系统工程研究所，上海 201109）

服务航天器超近程逼近失控目标的建模与控制

靳永强 张庆展 康志宇 唐平
（上海宇航系统工程研究所，上海 201109）

为在轨服务任务中实施对失控目标的安全逼近与对接，开展了服务航天器超近程逼近过程的动力学与控制研究。通过引入描述相对运动构型变化的期望相对位置矢量和位置误差矢量，推导了一种新颖的相对轨道误差动力学模型；考虑对接机构安装位置及安装误差，并结合相对姿态动力学模型，建立了逼近过程的相对姿态轨道耦合动力学模型；根据逼近路径约束条件，设计了逼近过程的期望相对位置矢量导引律；基于相对姿态轨道一体化耦合动力学模型，设计了考虑未知有界干扰的自适应时变滑模控制律并利用李雅普诺夫稳定性理论证明了闭环系统的全局稳定性。仿真结果表明，设计期望相对位置矢量导引律的方法能够实现逼近过程的相对运动构型变化控制，并且所设计的自适应时变滑模控制律具有较高的控制精度。

失控目标；控制；期望相对位置矢量；服务航天器

1 引言

对在轨失控航天器捕获后进行维修、补给或移除等在轨服务，可延长其工作寿命、提升工作能力或减少空间碎片数量，对航天产业可持续发展具有重要意义。失控航天器的对接口随其姿态翻滚而运动，这对服务航天器超近程逼近至对接过程的建模和控制提出了新的要求。在此过程中，需控制服务航天器沿被动对接口方向逼近目标航天器，同时跟踪其姿态变化使主动对接口指向被动对接口。显然，此过程中服务航天器相对目标的位置和姿态是耦合的［1］。

相对姿态和轨道耦合动力学与控制是伴随空间服务操作任务需求提出的。文献［2］推导了编队飞行中从星相对主星的姿轨耦合动力学模型；文献［3］研究卫星编队飞行控制时，提出期望编队点概念，并推导了相对轨道误差动力学模型［3］。针对姿态稳定目标的超近程逼近控制研究较多［4－6］。逼近失控目标时，服务航天器相对目标的位置和姿态需同时跟踪目标的姿态进行快速变化，提高了对建模与控制要求。文献［7］采用θ－D次优控制方法研究了挠性航天器接近自由翻滚目标的控制问题，未考虑系统干扰和不确定性；文献［8］采用模型预测控制方法研究了与旋转平台交会对接的位置控制问题，未考虑姿态部分；文献［9］采用θ－D次优控制算法设计了航天器间近距离相对运动的姿轨耦合控制器，但在动力学建模中未考虑对接口的安装位置；文献［10］针对与失控目标交会对接近距离段的姿轨耦合控制问题，设计了干扰自适应滑模控制器。时变滑模控制克服了常规滑模控制在系统相轨迹到达滑模面之前鲁棒性弱的缺点，在航天器控制中有广泛研究［11－12］。

文章综合考虑在轨服务操作任务的多样性及对相对运动构型需求的灵活性，在动力学建模中引入描述相对运动构型变化的期望相对位置矢量和位置误差矢量，推导了一种新颖的相对轨道误差动力学模型。该模型将航天器间的相对位置跟踪控制分解为描述相对位置变化的期望相对位置矢量设计和由位置误差矢量描述的二阶系统调节器设计。根据逼近路径的约束条件，设计逼近过程的期望相对位置矢量导引律，控制航天器间的相对运动构型变化。考虑对接口安装位置及误差，推导了非点质量模型的相对姿轨一体化耦合动力学模型。基于此耦合动力学模型，设计了考虑未知有界干扰的自适应时变滑模控制律，并利用李雅普诺夫稳定性理论证明了闭环系统的全局稳定性。仿真中考虑工程实际需求，设置了逼近停泊点和启动缓冲过程。

2 问题描述

为便于问题描述，引入相对轨道坐标系OT－xTyTzT：原点OT位于目标的质心，OTxT为地心与目标质心连线背离地心方向，OTzT为目标轨道面正法向，OTyT与OTzT、OTxT形成右手坐标系。Oi－xiyizi和Ob－xbybzb分别表示地心惯性坐标系和航天器本体坐标系［1］。

2.1 相对轨道动力学模型

服务航天器与目标之间的位置关系如图1所示。图1中，rt、rs分别为目标、服务航天器的位置矢量；ld和δr分别为服务航天器的期望相对位置矢量和位置误差矢量，用于描述航天器间的相对运动构型变化。则有关系式

结合惯性系中轨道动力学与式（1），在相对轨道系中建立相对轨道误差动力学模型为

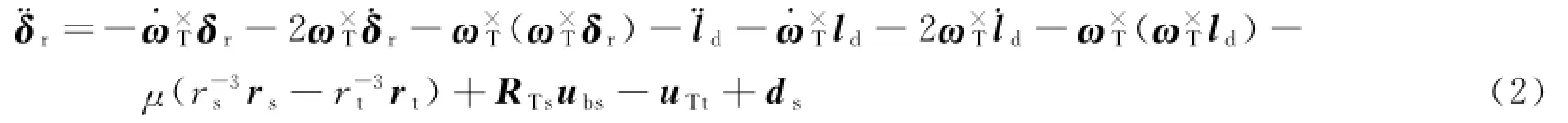
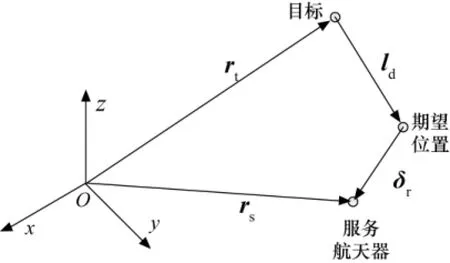
图1 服务航天器与目标之间的位置关系Fig.1 Position between servicing spacecraft and target

式（3）由位置误差矢量δr描述的相对轨道误差动力学模型的平衡状态是零状态，并且其控制量uo包含与期望相对位置矢量ld相关控制量。引入期望相对位置矢量ld和位置误差矢量δr，将航天器间的相对位置跟踪控制分解为描述相对运动构型变化的ld设计和由δr描述的二阶系统调节器设计，简化了相对位置运动构型的描述和控制器的设计。

式（3）描述的是将航天器看作质点的相对轨道误差动力学模型，而超近程逼近过程是控制两航天器对接口之间的相对状态。则需建立考虑对接口安装的相对轨道误差动力学模型。

图2中，rds、rdt分别为主、被动对接口的安装位置矢量，且，其中为期望安装位置矢量，δds、δdt为安装位置误差矢量；rdt／s为两对接口之间在相对轨道系中的位置矢量。则有关系式

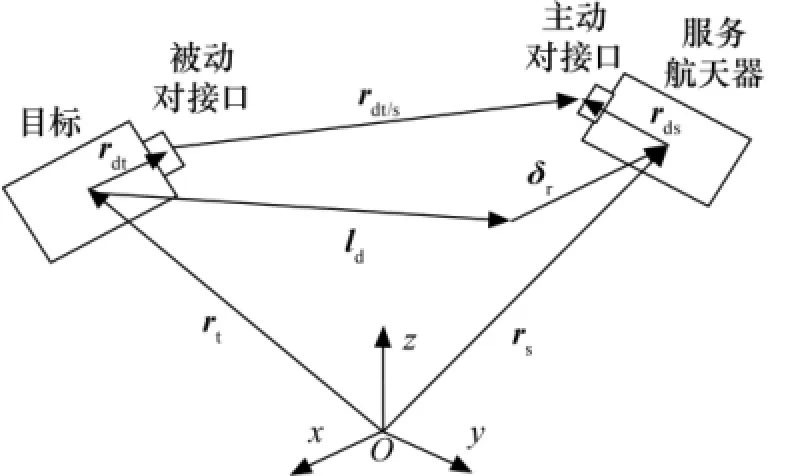
图2 两对接口间的位置关系Fig.2 Position between the two docking ports

式中 RTt、Rst分别为目标本体系到相对轨道系、服务航天器本体系的坐标转换矩阵。

2.2 相对姿态动力学模型

定义σst为采用修正罗德里格参数描述的服务航天器相对目标的姿态；ωst＝ωs－Rstωt为相对姿态角速度，其中ωs、ωt分别为服务航天器、目标本体相对惯性系的姿态角速度，则相对姿态运动学和动力学方程的具体表达式见文献［13］。结合文献［13］中的相对姿态运动学和动力学方程，可得类拉格朗日方程形式的相对姿态动力学模型为

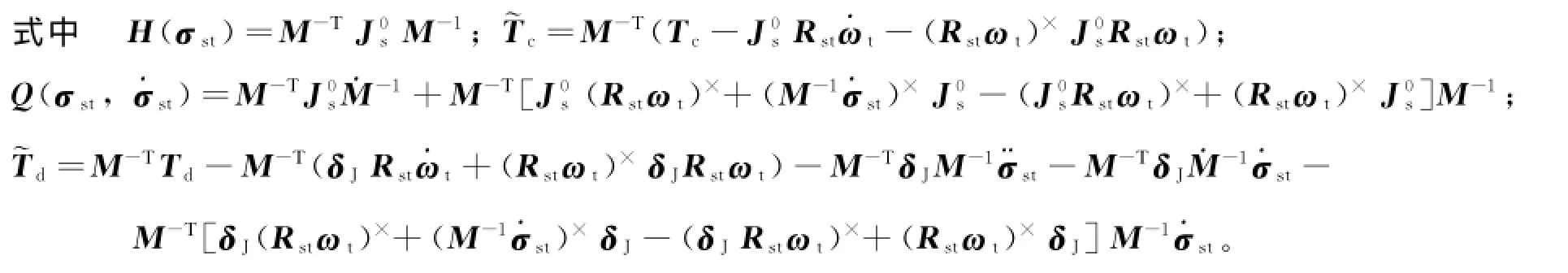
2.3 期望相对位置矢量导引律

为实现对失控目标的逼近至对接，需控制服务航天器沿被动对接口方向逼近目标航天器，同时跟踪其姿态变化使主动对接口沿逼近方向指向被动对接口。假设失控目标可向服务航天器提供其运动状态信息，或服务航天器利用自身设备可获取目标的运动状态信息。则在相对轨道系内设计期望相对位置矢量ld运动规律为

可根据任务需求设计l（t）的运动规律，如考虑逼近启动时的缓冲，引入指数函数设计为

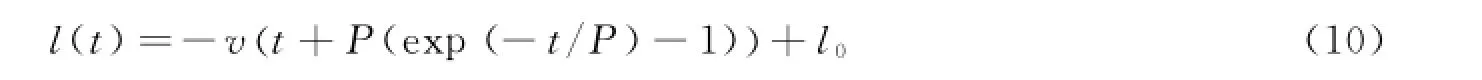
式中 P为缓冲时间常数；v为期望逼近速率；l0为期望相对位置的初始值。

式（5）和式（6）描述了超近程逼近失控目标至对接过程的相对位置误差和相对姿态动力学模型。式（7）描述了逼近过程的相对位置导引律。由此可知控制系统的目的是，设计相对轨道和姿态控制律，在式（7）给出的相对位置导引律下，使Δr→0，→0，σst→0，→0。

3 相对姿轨耦合控制律设计

由式（11）可知控制系统的目的是，设计相对姿轨一体化耦合控制律，使x→0， x→0。针对式（11）描述的服务航天器超近程逼近失控目标的相对姿轨耦合动力学模型，本节基于自适应方法和时变滑模思想给出一种自适应时变滑模耦合控制器。时变滑模保证了系统的全局鲁棒性；切换增益的自适应消除了控制器参数选择时需已知系统不确定性上界的要求。

假设闭环系统初始状态已知或可测，则根据等速度规律变化斜率的时变滑模面S定义为

式中 A＝diag（a1，a2，…，a6）和B＝diag（b1，b2，…，b6）为常值对角矩阵；T＞0为两种滑模面的切换时间；k＞0为滑模面的斜率。

S满足下列两个条件：

1）在初始时刻，系统的初始值位于滑模面上，即

2）T时刻滑模面满足连续平滑过渡，即

由式（13）和式（14）可得

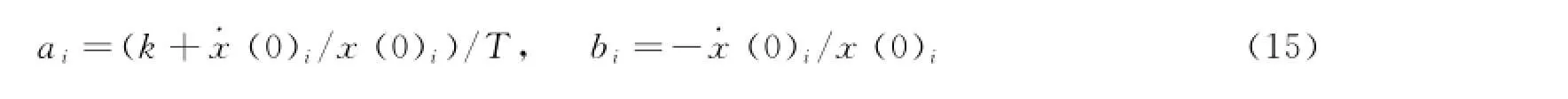
式中 x（0）i、（0）i分别为x（0）、（0）的元素，i＝1，2，…，6。

假设系统受到的环境干扰、对接机构安装位置误差以及服务航天器惯量不确定性等造成的复合干扰d有界，并假设d满足如下条件［13］：

式中 di＞0（i＝1，2，3）为干扰边界参数。

则设计相对姿轨耦合的自适应时变滑模控制律为

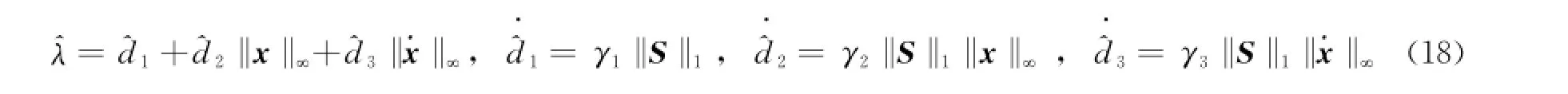
式中 γi＞0（i＝1，2）为自适应常数，决定了的自适应速度，＞0（i＝1，2，3）为干扰边界自适应参数。从式（18）可以看出，切换增益自适应机理为：根据系统状态偏离所设计滑模面的程度对切换增益进行在线调整。一旦状态偏离所设计滑模面，便对式（18）进行积分，不断增大切换增益值，直至系统状态收敛到所设计的滑模面上。

将式（17）代入 V可得

将式（18）代入式（20）可得

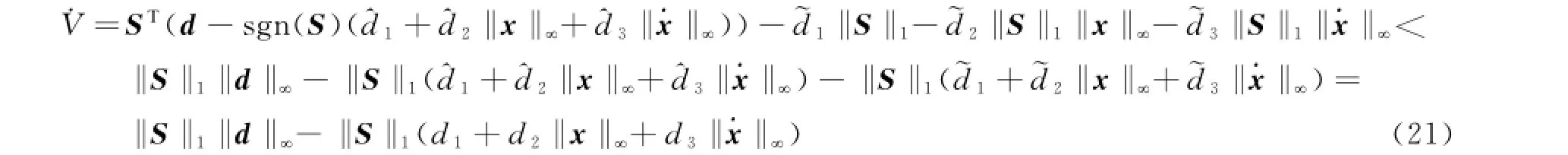
由式（21）并结合式（16）可知， V≤0是半负定的，因此V（t）是非增有界的。这说明S（t）、是有界的。令Q（t）＝－ V，对其从0到t进行积分，可得由V（0）和V（t）是有界的，可得

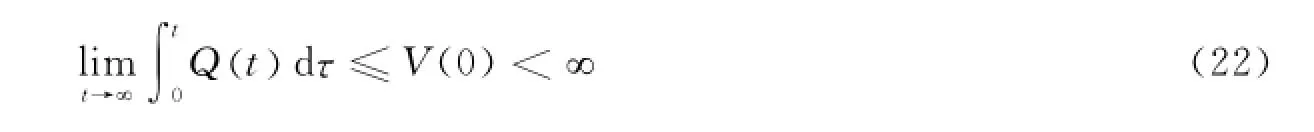
由式（22），根据Barbalat引理知，当t→!时，Q（t）→0。又由式（16）可推得，当t→!时，S（t）→0。直观上讲，由t→!时，S（t）→0并不能直接得到当t→!时→0，i＝1，2。但是，闭环系统的渐近稳定性可解释为：由自适应切换增益的计算式（18）可知，若‖S‖1≠0，则会一直增大，直到满足滑模到达条件 （即＞‖d‖!），从而，滑动模态会在有限时间内出现。此时，根据时变滑模函数的表达式（12）可得，系统跟踪误差x（t）渐近收敛，从而保证了整个闭环系统的渐近稳定性。

可得作用在服务航天器本体的控制加速度ubs和控制力矩Tc为

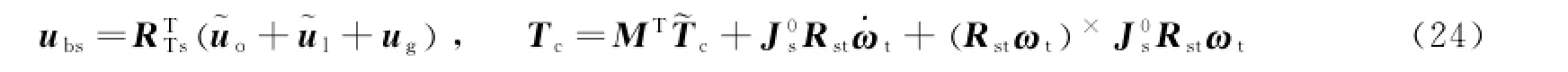
式（18）提供了一种估计系统干扰上界的方法，但其仅在“理想”滑模（即S（t）＝0）情况下有效。在实际工程应用中，由于外部扰动、模型不确定性及有限切换频率等因素影响，滑模函数无法严格为零。此时，由式（18）可知切换增益会持续增大直至无界。可采用sigma修正法来解决的漂移现象，同时为减小式（17）中的符号函数引起的抖振问题，用饱和函数来代替［15］。修正后的自适应律为

式中 τi＞0为较小常数，i＝1，2，3。

4 仿真验证

假设目标为GEO轨道上的失控航天器，其在绕最大主惯量轴z轴旋转的同时存在小幅章动。取三轴姿态旋转角速度分别为ωx＝0.005（°）／s、ωy＝0.01（°）／s和ωz＝0.2（°）／s；初始轨道参数为at＝42 164 137m、et＝0.005、it＝0.5°、Ωt＝10°、ωt＝20°和ft＝215°。

综合考虑工程实际中的逼近安全性、相对导航切换策略、服务航天器控制能力以及对接初始条件等因素，设计服务航天器期望相对距离l（t）的导引律为：假设服务航天器从距目标120m出发，以0.08m／s的速度开始逼近目标，在距目标30m处设置一停泊点，服务航天器停泊3min，然后以0.04m／s的速度逼近目标至对接。l（t）运动规律的具体表达式为

GEO航天器受到的环境干扰加速度一般在10－6m／s2数量级。考虑系统其他因素影响，取相对干扰加速为［3.1，4.0，3.6］T×10－5m／s2。取作用在服务航天器上的干扰力矩模型为［15］

式中 A0＝1.5×10－5Nm；ωs为服务航天器的轨道角速度。

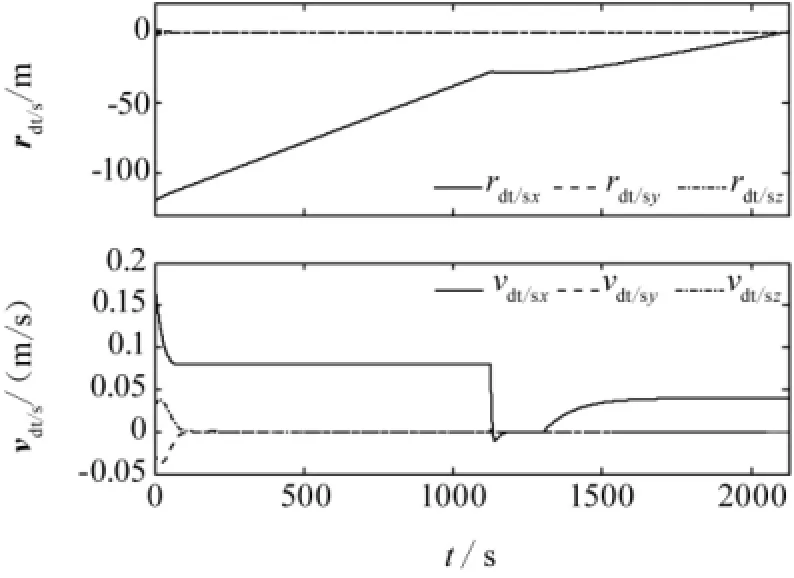
图3 目标本体系下的对接口间相对位置和速度Fig.3 Relative position and velocity between docking ports in target fixed body frame

图4 相对位置和速度误差曲线Fig.4 Errors of relative position and relative velocity

图5 相对姿态角和相对角速度误差曲线Fig.5 Errors of relative attitude angle and relative angular velocity

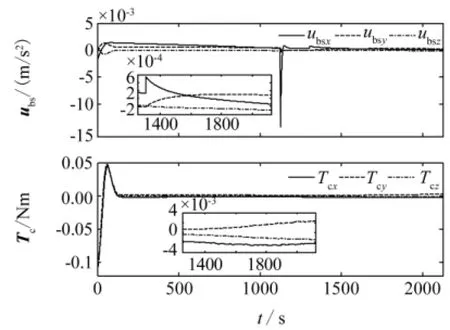
图6 控制加速度和控制力矩曲线Fig.6 Control acceleration and control moment

图7 相对轨道坐标系内服务航天器相对位置曲线Fig.7 Relative position of servicing spacecraft in the relative orbit coordinate system

由图3可见，在期望相对位置矢量ld导引下，服务航天器从距目标120m处沿被动对接口方向以0.08m／s的接近速度，经1 125s到达距目标30m的停泊点；180s后在指数函数导引缓冲下，以0.04m／s的速度逼近目标至对接。由图4可知，经过110s左右服务航天器对接口跟踪上期望相对位置状态（包括位置和速度）的变化。逼近初始和停泊初始时相对位置状态误差较大，由初始位置误差和逼近速度突变造成；而停泊结束后，由于指数函数的引导使得再次逼近平滑启动，相对位置状态误差较小；并且其他稳态跟踪时段相对位置稳态跟踪误差不大于0.005m，相对速度稳态跟踪误差不大于0.000 3m／s。由图5可看出，经过115s左右服务航天器跟踪上目标的姿态状态（包括姿态和角速度）变化，相对姿态角稳态跟踪误差不大于0.05°，相对角速度稳态跟踪误差不大于0.002（°）／s，并且停泊时段不影响相对姿态状态跟踪。由图6可得出，在服务航天器逼近初始和停泊初始时，控制加速度和力矩相对较大，在完成对目标位置和姿态跟踪后迅速减小，并以相对较小的控制加速度和力矩维持相对位置状态和相对姿态状态的稳态跟踪。图7给出了逼近过程的相对轨迹，显示逼近轨迹为螺旋曲线。仿真结果表明文章考虑对接口安装位置及误差而推导的超近程逼近失控目标的数学模型是正确的，考虑惯量不确定性和有界干扰设计控制律是有效的，并具有一定的鲁棒性。

5 结束语

服务航天器超近程逼近失控目标至对接的过程中相对姿态和轨道是耦合的。文章考虑对接口安装位置及安装误差，推导了相对姿轨一体化耦合动力学模型。通过引入描述相对运动构型变化的期望相对位置矢量和位置误差矢量，将相对轨道跟踪控制问题转化为调节器设计问题。考虑相对姿轨耦合性及未知有界干扰影响，设计了自适应时变滑模控制律。仿真中结合工程实际，设置服务航天器逼近目标的停泊点和考虑逼近启动过程缓冲。数学仿真结果表明，文章所建模型和所设计的控制算法是有效的，并具有较好的控制性能。通过期望相对位置矢量来控制相对运动构型运动的方法，同样适用于其他空间操作的控制实现，如航天器的空间快速绕飞及编队飞行队形保持等。

［1］ LU W，GENG Y H，CHEN X Q，et al.Relative position and attitude coupled control for autonomous docking with a tumbling target［J］.International Journal of Control and Automation，2011，4（4）：1－22.

［2］ PAN H，KAPILA V.Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics［C］.Proceedings of the 40th IEEE Conference on Decision and Control，Orlando，Florida，December，2001.

［3］ XING G Q，PARVEZ S A.Implementation of autonomous GPS guidance and control for the spacecraft formation flying［J］.Frontier Science，2008，2（5）：56－66.

［4］ SUBBARAO K，WELSH S J.Nonlinear control of motion synchronizations for satellite proximity operations［J］.Journal of Guidance，Control，and Dynamics，2008，31（5）：1284－1294.

［5］ 朱志斌，李果，何英姿，等.基于滚动优化的模块航天器姿轨协同控制 ［J］.中国空间科学技术，2011，31（2）：1－8.

ZHU ZHIBIN，LI GUO，HE YINGZI，et al.Relative cooperative attitude and position control of fractioned spacecraft based on iterative optimization［J］.Chinese Space Science and Technology，2011，31（2）：1－8.

［6］ GAO X Y，YAO W，LIU H.An optimal control approach to robust control of spacecraft rendezvous system on elliptical orbit［C］.31st Chinese Control Conference，Hefei，2012.

［7］ XIN M，PAN H J.Nonlinear optimal control of spacecraft approaching a tumbling target［J］.Aerospace Science and Technology，2011，15（2）：79－89.

［8］ HYEONGJUN P，STEFANO D C，ILYA K.Model predictive control for spacecraft rendezvous and docking with a rotating tumbling platform and for debris avoidance［C］∥Proceeding of the 2011 American Control Conference，San Francisco，2011.

［9］ 李鹏，岳晓奎，袁建平.基于θ－D方法的在轨操作相对姿轨耦合控制 ［J］.中国空间科学技术，2012，32（4）：8－14.

LI PENG，YUE XIAOKUI，YUAN JIANPING.Coupled control of relative position and attitude based onθ－D technique for on－orbit operations［J］.Chinese Space Science and Technology，2012，32（4）：8－14.

［10］ 姜博严，胡庆雷，石忠，等.与翻滚目标近距离交会对接的相对姿轨耦合控制 ［J］.宇航学报，2014，35（1）：54－60.

JIANG BOYAN，HU QINGLEI，SHI ZHONG，et al.Relative position and attitude coupled controller design for approaching and docking with a freely tumbling target［J］.Journal of Astronautics，2014，35（1）：54－60.

［11］ JIN Y Q，LIU X D，QIU W，et al.Time－varying sliding mode controls in rigid spacecraft attitude tracking［J］.Chinese Journal of Aeronautics，2008，21（4）：352－360.

［12］ CONG B L，LIU X D，CHEN Z，et al.Time－varying sliding mode control for spacecraft attitude tracking maneuvers with a quadratic cost［C］∥Proceedings of the 30th Chinese Control Conference，Yantai，2011.

［13］ XING G Q，PARVEZ S A.Relative attitude kinematics ＆dynamics equations and its applications to the general spacecraft attitude state tracking control problem［J］.Frontier Science，2008，2（7）：26－34.

［14］ MENG Q，ZHANG T，SONG J Y.Autonomous fault－tolerant time－varying attitude tracking control of uncertain flexible satellite［C］.10th IEEE International Conference on Control and Automation，Hangzhou，2013.

［15］ WHEELER G，SU C Y，Stepanenko Y.A sliding mode controller with improved adaption laws for upper bounds on the norm of uncertainties［J］.Automatica，1998，34（12）：1657－1661.

Modeling and Controlling for Servicing Spacecraft Approaching a Tumbling target in Close Proximity

JIN Yongqiang ZHANG Qingzhan KANG Zhiyu TANG Ping
（Aerospace System Engineering Shanghai，Shanghai 201109）

To insure the safety of autonomous approaching and docking of a tumbling target in on－orbit servicing missions，the dynamics and control for servicing spacecraft approaching in close proximity was researched.By introducing the desired relative position vector and the position error vector，which figured the relative motion configuration，a novel relative position dynamic model was derived.Considering the installation location and errors of docking mechanisms，the coupled relative position and attitude dynamic model of approaching was established.The motion law of the desired relative position vector was designed under the constraint of approaching path.Based on the integrated coupled dynamic model and considering unknown boundary interferences，the adaptive time－varying sliding mode control law was proposed，and the close－loop system was proved to be steady by using of the Lyapunov stability theory.Simulation results show that the approach of designing the desired relative position vector can control the configuration changes of the relative motion，and the adaptive time－varying sliding mode control law achieves a comparatively high precision.And the coupled model and the control law are effective with perfect performance.

Tumbling target；Control；Desired relative position vector；Servicing spacecraft

10.3780／j.issn.1000－758X.2015.03.001

（编辑：王晓宇）

上海市科学技术委员会（13QB1404000，14XD1423400）资助项目

2015－01－22。

收修改稿日期：2015－03－10

靳永强 1981年生，2008年获北京理工大学控制理论与控制工程专业博士学位，高级工程师。研究方向为航天器总体设计和姿态轨道控制。