船舶在横浪中的横摇运动及其稳定性研究

傅晓斌

(南通航运职业技术学院，江苏南通226010)

船舶在横浪中的横摇运动及其稳定性研究

傅晓斌

(南通航运职业技术学院，江苏南通226010)

摘要:以规则横波下的船舶稳定性为研究对象，对船舶在横浪中的横摇运动及其稳定性进行深入研究。本文首先描述船舶横摇运动的非线性方程的建立方法，然后对横浪中船舶的横摇运动稳定性进行分析。分别介绍基于Lyapunov指数法的船舶混沌状态识别方法和基于Melnikov数值积分法的船舶全局稳定性分析方法。仿真实验结果表明，本文介绍的方法能够更好地了解不同激励下船舶的运动状态，稳定性判断方法具有很高的正确性。

关键词:横摇运动;稳定性;非线性方法

Research on amplitude rolling and stability of a ship in longitudinal wave

FU Xiao-bin
(Nantong Shipping College，Nantong 226010，China)

Abstract:In this paper the stability of a ship in longitudinal wave was studied，the amplitude rolling movement and stability were researched．Firstly，the nonlinear rolling equation for descripted the ship amplitude rolling movement on regular beam seas was introduced，then the ship rolling motion stability was analyzed，the chaotic state identification method based on Lyapunov index method and numerical integral method based on Melnikov global stability analysis method of the ship was introduced separately．The simulation resultes shown that the method introduced in this paper was a better way to understand the motion of the ship under different incentive，and had very high accuracy．

Key words:amplitude rolling; stability;nonlinear dynamic methods

0　引言

随着海上经济贸易的繁荣，海上运输业不断发展，船舶安全问题越来越受到人们的关注，而在船舶安全中，船舶的稳定性一直是研究的重点。船舶稳定性是指在外力干扰影响下不会发生倾覆，并且在干扰消失后能够恢复到正常状态的能力。通过研究船舶在风、浪等环境下运动的稳定性及其倾覆机理，对于保障船舶安全航行具有非常重要的理论意义和现实价值。在本文中，以规则横波下的船舶稳定性为研究对象，分别研究了船舶横摇运动［1］的非线性运动方程，非线性运动响应，混沌状态识别及运动稳定性分析。

1　非线性方程的建立

船舶横摇运动属于一种非常复杂的、非线性的动力学行为，因此本文通过建立非线性方程的方法来研究船舶在规则横波中的运动行为［2］。非线性方程的建立方法在线性方程基础上，再考虑非线性的影响因素。

船舶横摇运动的参考坐标系如图1所示。其中，坐标系XGZ为联船坐标，表示船舶本身; G为船舶

的重心; XbOZb为随船坐标。船舶的每一微段重力距可表示为:

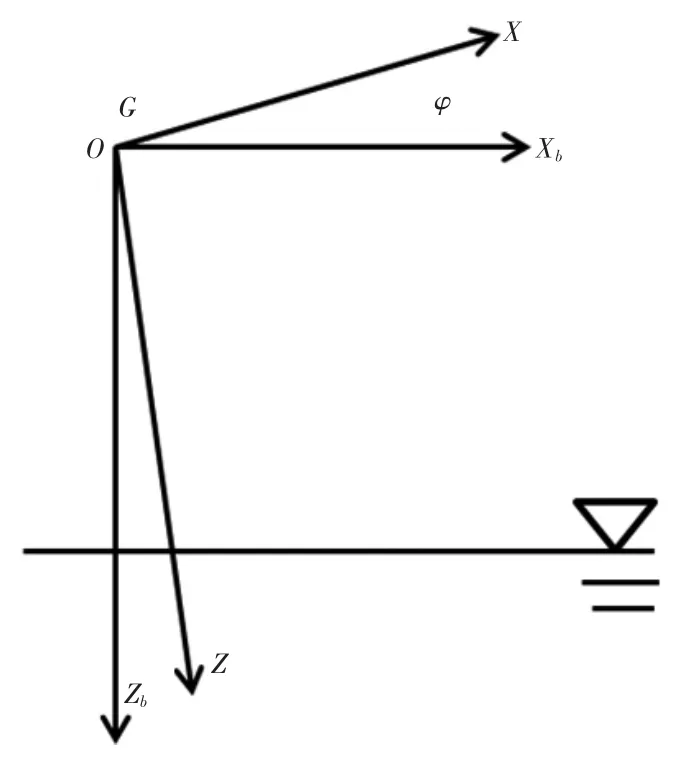
图1　坐标系Fig.1　Coordinate systems

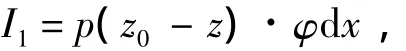
式中: p为微段重量; z为微段重心中的垂向坐标。

浮力力矩可表示为:

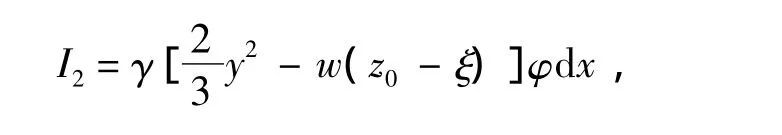
式中: z0为船舶中心中的垂向坐标;ξ为微段浮心中的垂向坐标;γ为水的重度。

阻尼力矩可表示为:

式中φ·为船舶横摇的角速度。

微段惯力矩可表示为:

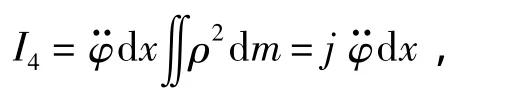
式中: j为该微段对O轴横摇转动的惯性矩;φ·为船舶横摇的角速度。

根据每一微段间的作用力相互平衡，因此有:

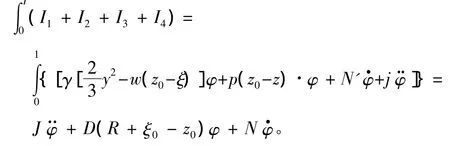
式中: D为排水量; R为稳心的半径;ξ0为船舶浮心中的垂向坐标; N为阻尼系数; J为转动惯量。由于，所以静水中，船舶横摇运动微分方程可表示为:

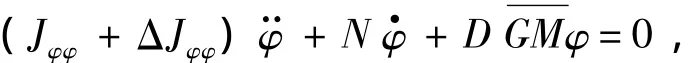
式中:ΔJφφ为附加的转动惯量;为横摇的出稳性高。

设横波中，波浪干扰的表达式为:

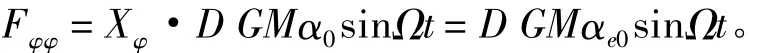
式中:αe0= Xφα0为有效波的倾角振幅; Xφ为修正系数。

因此横波中，船舶横摇运动微分方程可表示为:

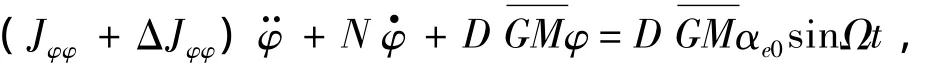
考虑的非线性干扰因素如表1所示。

表1　干扰因素Tab.1　Interference factors

在横波中船舶横摇运动微分方程的基础上，其非线性方程为:

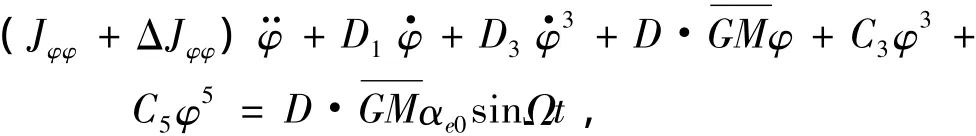
将上式等号两侧同时除以Jφφ+ΔJφφ后，得:

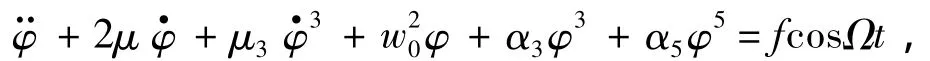
2　稳定性分析

2.1混沌态的识别方法

混沌［3］是一种非线性运动形式，在船舶横摇运动的非线性分析中，混沌态的出现往往是导致船舶倾覆的主要原因，所以，在本文中，将是否出现混沌态作为船舶稳定性的依据，如果出现了混沌态，则判定船舶运动为不稳定的;如有没有出现混沌态，那么则判定船舶运动具备稳定性。混沌态的识别方法见表2。

表2　识别方法Tab.2 Identification methods

表2中的方法容易受到图形质量、判断者经验影响，其识别的准确率往往不高，为了减少误判率，文本采用基于Lyapunov指数［4］法的定量分析方法进行混沌态的识别。

设n维连续系统为:

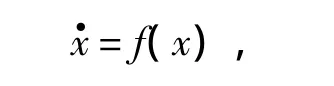
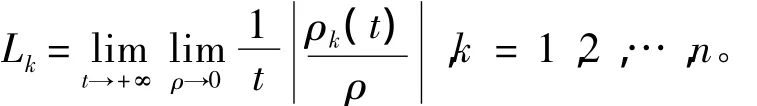
式中ρ为流的向量空间中半径为ρ的球。基于Lyapunov指数的混沌态判断方法如下:

2.2稳定性分析

本文利用Melnikov函数［5］来分析横波中船舶的稳定性。

设平面中，非自治系统为:

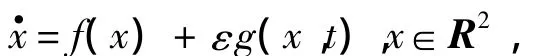
式中:ε为参数; g为干扰。当ε= 0时，

而双曲鞍点ps可通过对其的同宿轨道xh(t－τ)积分求得:

设Melnikov函数的表达式为:

其中∧的定义为:

由于若Melnikov函数存在简单零点，那么有，M(t0) = 0，M'(t0)≠0，进而，稳定流形与不稳定流形必然会相交，因此，可以通过判断稳定流形与不稳定流形必是否相交来分析运动稳定性。

在上一节中介绍的非线性横摇运动方程中，将恢复力矩取3次方为例，则:

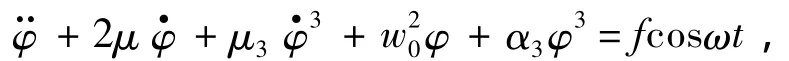
无因次化后得:

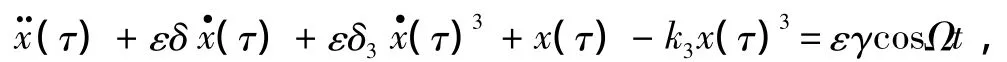
即:

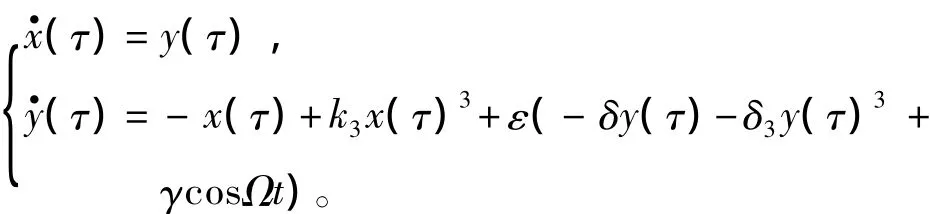
当ε= 0时，上式变为:

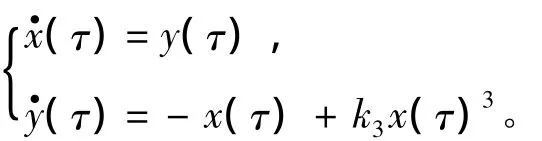
此时，上式变为了Hamilton系统，其Hamilton量为:

而异宿轨道方程为:

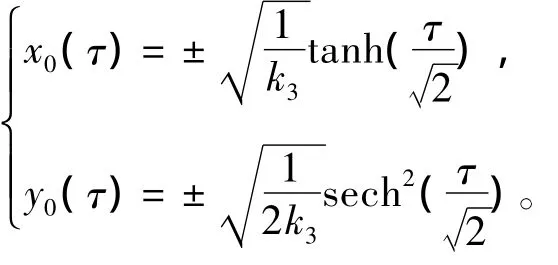
而该系统的Melnikov函数为:

将异宿轨道方程代入上式中得:

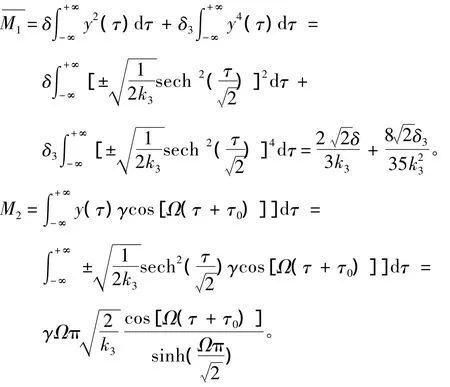
从而Melnikov函数可表示为:

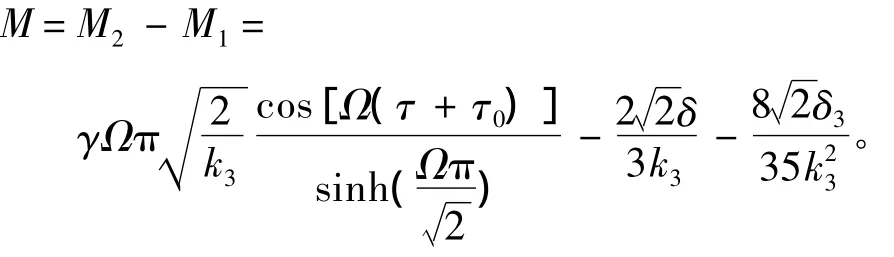
另Melnikov函数为0，得到:

式中:γcritical为临界条件。

在仿真实验中，对5次方非线性系统的表达式进行稳定性分析。5次方非线性横摇运动方程无因次化后为:

采用Melnikov函数数值积分法对上式进行解析，设定的相关参数如表3所示。

表3　参数Tab.3　Parameters

通过数值积分方法求解后得γcritical= 0.1995，全局稳定性如图2所示。

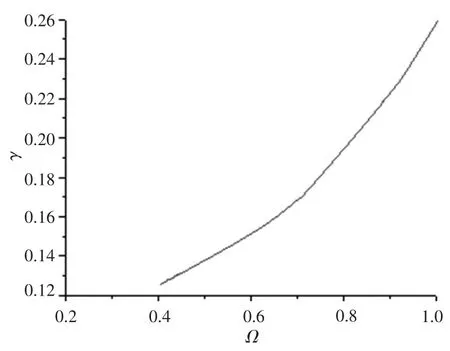
图2　稳定性Fig.2　Stability for the model ship

3　结语

本文对船舶在横浪中的横摇运动及其稳定性进行了研究。首先介绍了用来描述舶横摇运动的非线性方程的建立方法，然后对横浪中，船舶的横摇运动稳定性进行了分析，分别介绍了基于Lyapunov指数法的船舶混沌状态识别方法和基于Melnikov数值积分法的船舶全局稳定性分析方法。仿真实验结果表明，本文介绍的方法能够更好地了解不同激励下船舶的运动状态，具有很高的正确性。

参考文献:

［1］夏志平，文逸彦，杨松林，等．新型三体船横摇运动分析［J］．舰船科学技术，2014，36(2) :33－36，59．XIA Zhi-ping，WEN Yi-yan，YANG Song-lin，et al．Think on the development in autonomous underwater vehicles［J］．Ship Science and Technology，2014，36(2) :33－36，59．

［2］The Specialist Committee on Stability in Waves．Final Report and Recommendations to the 25th ITTC Proceedings of 25th ITTC，2008，Fukuoka．

［3］刘延柱，陈立群．非线性振动［M］．北京:高等教育出版社，2001:57－126．

［4］刘禀正，彭建华．非线性动力学［M］．北京，高等教育出版社，2004．

［5］李亚峻，李月．用Melnikov函数的数值积分法估计混沌阈值［J］．系统仿真学报，2004，16(12) :2692－2695．

作者简介:傅晓斌(1981－)，男，硕士，讲师，研究方向为船舶建造检验。

收稿日期:2014－10－17;修回日期: 2015－01－30

文章编号:1672－7649(2015) 07－0128－04doi:10.3404/j.issn.1672－7649.2015.07.029

中图分类号:U665．26

文献标识码:A